达朗贝尔原理课件 18页

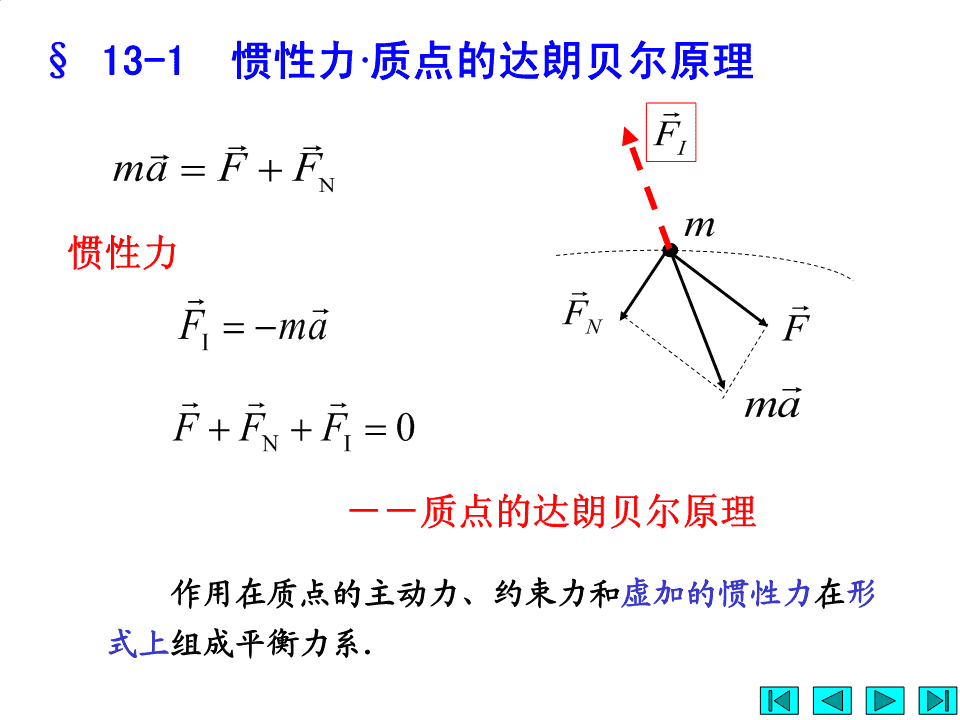
第十三章达朗贝尔原理 §13-1惯性力·质点的达朗贝尔原理FImaFFNm惯性力FFmaNFImaFFF0NI－－质点的达朗贝尔原理作用在质点的主动力、约束力和虚加的惯性力在形式上组成平衡力系. §13-2质点系的达朗贝尔原理1.质点系的达朗贝尔原理质点系m,m,,m12n()e()i()e()i()e()iF1,F1,F2,,F2,,Fnn,F引入第i个质点的惯性力FmaIiii(e)(i)FFF0iiIi平衡力系(e)(i)(e)(i)(e)(i)F,F,F,F,F,F,,F,F,FIn11I122I2nn 力系平衡条件(e)(i)FiFiFIi0(e)(i)mo(Fi)mo(Fi)mo(FIi)0注意内力力系自相平衡(i)Fi0(i)mo(Fi)0推得(e)FiFIi0(e)mo(Fi)mo(FIi)0－－质点系的达朗贝尔原理作用在质点系上的外力与虚加在每个质点上的惯性力在形式上组成平衡力系—平衡方程形式的动力学方程. 2.质点系统动力学方程(e)FxFIx0F(e)F0xIRx()FyFIy0F(e)F0yIRy(e)FF0(e)zIzFF0zIRzm(F(e))m(F)0xixIim(F(e))M0xiIxm(F())m(F)0yiyIim(F())M0yiIym（F(t)）m(F)0zizIi(e)m（zFi）MIz0FI1,FI2,,FInFIR,MIO向O点简化 3.惯性力系的主矢和主矩FI1,FI2,,FInFIR,MIO向O点简化dvddKimvFIRFIimiiidtdtdtdvdMm(F)r(mi)rmvIOOIiiiiiidtdtddLm(mv)OOiidtdt代入质点系的达朗贝尔原理dK(e)Fi0dt－－质点系的达朗贝尔原理dL=动量定理+动量矩定理(e)Omo(Fi)0dt §13-3刚体惯性力系的简化1.平移miriaiaCrCmFI1,FI2,,FInFIR,MIO,FFmamaIRIiiiCMIOmO(FIi)rimiai(miri)aCmrar(ma)rFCCCCCIROCM0IC 2.定轴转动（平面）FI1,FI2,,FInFIR,MIO向转轴O简化tnatran2rtnaiaiaiiiiiFIiFIiFIiFIRFIimiaimaCtnMIOmO(FIi)mO(FIiFIi)tmO(FIi)2(miri)Jz 例13-1如图所示,电动绞车安装在梁上,梁的两端搁在支座上,绞车与梁共重为P.绞盘半径为R,与电机转子固结在一起,转动惯量为J,质心位于转轴O处.绞车以加速度a提升质量为m的重物,其它尺寸如图.求：支座A，B受到的附加约束力. MIO解:FFAB1.取整体为研究对象FImaMIOJF2.列平衡方程IMB00mgl2FlI2Pl3MIOFlA1l2Fy0FAFBmgPFI03.运动学补充方程aRmgl2Pl3aJFAml2l1l2l1l2R静约束力mgl1Pl1l2l3aJFBml1l1l2l1l2R mgl2Pl3aJFAml2l1l2l1l2Rmgl1Pl1l2l3aJFBml1l1l2l1l2R附加约束力（动约束力）为aJFAml2l1l2RaJFBml1l1l2R 3.平面运动FI1,FI2,,FInFIR,MIC向质心简化FIRFIimiaiMaCtnaaaaiCiCiC,tnFmaFFIiiCIiCIiCtnMICmC(FIi)mC(miacFIiCFIiC)tmC(FIiC)2(miriC)JC 例13-2已知：均质圆盘mR1,,纯滚动.均质杆l2,Rm2.求：F多大,能使杆B端刚好离开地面?纯滚动的条件? 解:刚好离开地面时,B端地面约束力为零.１．研究整体Fma,MJ,FmaIA1AIAAIC2CFx0FFsFIAFIC0MD0,FRFIARMIAFICRsin30m2gRcos300Fy0FNP1P20 ２．研究AB杆MA0FICRsin30m2gRcos300３．运动学补充方程aRaCaAA33Fm1m23gFsm1g22FfFfmmgssNs12F3ms1fsF2mmN12 hF2F1FN2l2mgl1FN1利用动静法分析在刹车过程中，前、后轮哪一个轮容易“抱死”。 例10-1飞轮质量为m，半径为R，以匀角速度ω转动。设轮缘较薄，质量均匀分布，轮辐质量不计。若不考虑重力的影响，求轮缘横截面的张力。 解：1.取四分之一轮缘为研究对象n2FmamRgiiii2.列平衡方程Fx0FgicosiFA0m2RmdsRdi22m2mRFRcosdA0222mRFB2