分析力学-4达朗贝尔原理及其应用 19页

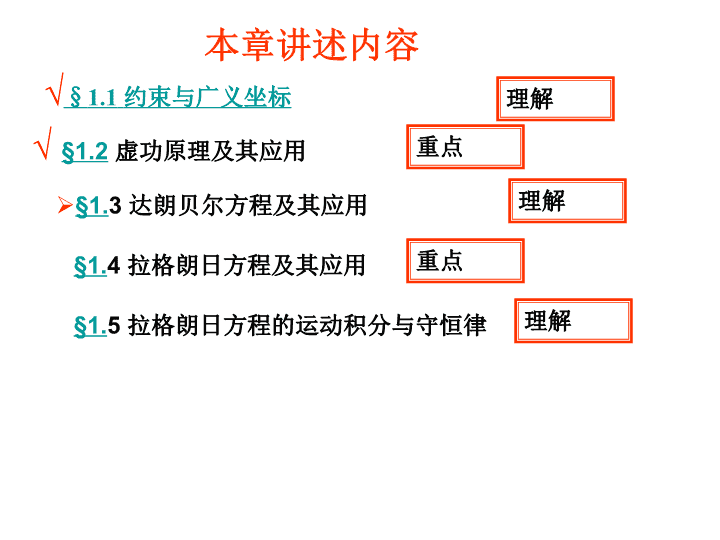
√§1.1约束与广义坐标√§1.2虚功原理及其应用§1.3达朗贝尔方程及其应用§1.4拉格朗日方程及其应用§1.5拉格朗日方程的运动积分与守恒律本章讲述内容重点重点理解理解理解 §1.3达朗贝尔方程(动力学普遍方程）这一节将通过达朗贝尔原理与虚功原理的结合，给出动力学普遍方程即：达朗贝尔方程。它们是分析力学的基础，是解决非自由质点系动力学问题的最一般原理。一、达朗贝尔原理（质点和质点系）二.达朗贝尔方程及其应用达朗贝尔人物简介 法国著名的物理学家、数学家和天文学家，一生研究了大量课题，完成了涉及多个科学领域的论文和专著，其中最著名的有八卷巨著《数学手册》、力学专著《动力学》、23卷的《文集》、《百科全书》的序言等等。达朗贝尔达朗贝尔生平达朗贝尔的科学成就 达朗贝尔原理是用静力学平衡的观点解决动力学问题，又称为动静法。一、达朗贝尔原理（质点和质点系）1、质点达朗伯原理对单个质点所受主动力为,约束力为，由牛顿第二定律：令，称为达朗伯惯性力，则上式可表示为：即主动力、约束力及达朗伯惯性力构成平衡力系。质点的达朗贝尔原理法国科学家达朗伯（贝尔）于1743年提出的 动力学问题静力学问题动静法通过在质点上虚加惯性力作用在质点上的主动力、约束力与惯性力构成一平衡力系。 主动力+约束力+惯性力=动平衡力系直角坐标系自然坐标系质点的达朗贝尔原理 达朗伯原理是在惯性系中写出的；它并没有改变动力学问题的性质。因为质点实际上并不是受到力的作用而真正处于平衡状态，而是假想地加在质点上的惯性力与作用在质点上的主动力、约束力在形式上构成平衡力系。达朗伯惯性力是在惯性系中引入的，它取决于质点自身的加速度,不是真正的惯性力；而作用在各质点上的惯性力则与所采用的非惯性系的加速度相关。说明： 例1:飞球调速器以等角速度转动，已知:锤重力P，飞球A、B均重G，各联杆长l。试求:A、B在转动时的张角。惯性力:[A]:[C]:得:得:wjBAC解:jAC 对由n个质点所组成的力学体系对第i个质点：*对系统进行累加：对*式左叉乘并对系统累加：质点系的达朗伯原理：作用在质点系上的所有外力与虚加在各质点上的惯性力在形式上构成平衡力系。由静力学平衡理论知，空间任意力系平衡的必要与充分条件是力系的主矢量和对任一点的主矩均等于零。2、质点系达朗伯原理 说明：①达朗伯原理仅对建立动力学方程提出了新的线索，但并未对求解运动微分方程增加任何新的东西；②对系统所得到的两个公式实际是质点系的质心运动定理和对固定点角动量定理的另一种表示。 二、达朗贝尔方程及其应用由质点系达朗贝尔原理：1、达朗贝尔方程—动力学的普遍方程两边点乘：当系统所受约束均为理想约束时，称为有效力。达朗贝尔方程（动力学普遍方程）即：在理想约束下，质点系所受有效力的虚功之和为零。 当系统所受约束均为理想约束时，有效力的虚功之和为零。说明：①动力学普遍方程与虚功原理相比较有以下推广；a.主动力推广到有效力；b.静力学推广到了动力学；达朗贝尔方程（动力学普遍方程）②此式仍是对惯性系成立；③动力学普遍方程主要应用于已知主动力求解系统运动规律，要正确分析主动力和虚加的达朗伯惯性力以及它们作用点的虚位移，正确计算相应的虚功。 在应用动力学普遍方程求解复杂质点系问题时，仍然是矢量微分方程组，如何将复杂的惯性力系表示成简洁方式，普遍方程中并没有给出，因此求解非常不便。并不是独立的变分；不能由动力学普遍方程直接求解！④解析形式：任一瞬时，作用在受理想约束的质点系上的主动力与惯性力在质点系任意虚位移中的元功之和为零。2、达朗贝尔方程—动力学的普遍方程应用举例 例1：一套滑轮系统悬挂两个重物。设绳和滑轮质量不计,绳不可伸长。试求:重力为P1的物体的加速度a1。解:自由度1解题步骤：1、运动分析，确定自由度；虚位移分析；2、受力分析（包括惯性力）；3、列写方程；4、确定虚位移之间的关系，运动关系；5、求解。 例2：调速器稳定在b时，试求与b关系,弹簧原长为2l。解:2em1gm1gllllkm2gbxy自由度1aa取广义坐标b mAgmBg例3：三棱柱A沿三棱柱B的光滑斜面下滑，A和B的质量各为mA、mB。试求:三棱柱B的加速度。解:xBxA自由度2 ABC例4：图示系统在铅垂平面内运动，各物体的质量均为m，圆盘的半径为R，绳索与圆盘无相对滑动。试求滑块的加速度和圆盘C的角加速度。ABC解：运动分析应用动力学普遍方程受力分析 ABC系统的虚位移ABC由动力学普遍方程得： ABC系统的虚位移ABC或令