内蒙古呼伦贝尔市阿荣旗第一中学2019_2020学年高二数学下学期3月月考试题文.doc 9页

内蒙古呼伦贝尔市阿荣旗第一中学2019-2020学年高二数学下学期3月月考试题文考试时间120分钟，分值150分一．选择题（每题5分，共60分）1.已知复数z满足条件：（1+2i）z=1，则z对应的点位于（　　）A.第一象限B.第二象限C.第三象限D.第四象限2.点M的直角坐标（，-1）化成极坐标为（　　）A.（2，）B.（2，）C.（2，）D.（2，）3.“e是无限不循环小数，所以e为无理数．”该命题是演绎推理中的三段论推理，其中大前提是（　　）A.无理数是无限不循环小数B.有限小数或有限循环小数为有理数C.无限不循环小数是无理数D.无限小数为无理数4.设某中学的高中女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（x，y）（i=1，2，3，…，n），用最小二乘法近似得到回归直线方程为=0.85x-85.71，则下列结论中不正确的是（　　）A.y与x具有正线性相关关系B.回归直线过样本的中心点C.若该中学某高中女生身高增加1cm，则其体重约增加D.若该中学某高中女生身高为160cm，则可断定其体重必为5.i是虚数单位，+++…+=（　　）A.1B.C.D.-6.在极坐标系中，圆ρ=4cosθ(ρ∈R)的圆心到直线(ρ∈R)的距离是（　　）A.B.2C.1D.27.极坐标方程ρ=sinθ+cosθ表示的曲线是（　　）A直线B圆C椭圆D抛物线8.给出下列结论：-9- （1）在回归分析中，可用相关指数的值判断模型的拟合效果，越大，模型的拟合效果越好；（2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；（3）在回归分析中，可用相关系数r的值判断模型的拟合效果，r越大，模型的拟合效果越好；（4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高．以上结论中，正确的有（　　）个．A.1B.2C9.观察下列一组数据=1，=3+5，=7+9+11，=13+15+17+19，…则从左到右第一个数是（　　）A.91B.89C.55D.4510.吸烟与患病这两个分类量计中，下列说法正确的是　　）A.若的观测值为k=6.635，我们有99%的把握认为吸烟与患肺病有关系；那么在100个吸烟的人中必有99人患有肺病B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推判出现错误D.以上三种说法都不正确11.对于给定的样本点所建立的模型A和模型B，它们的残差平方和分别是，，的值分别为，，下列说法正确的是（　　）A.若＜，则＜，A的拟合效果更好B.若＜，则＜，B的拟合效果更好C.若＜，则＞，A的拟合效果更好D.若＜，则＞，B的拟合效果更好-9- 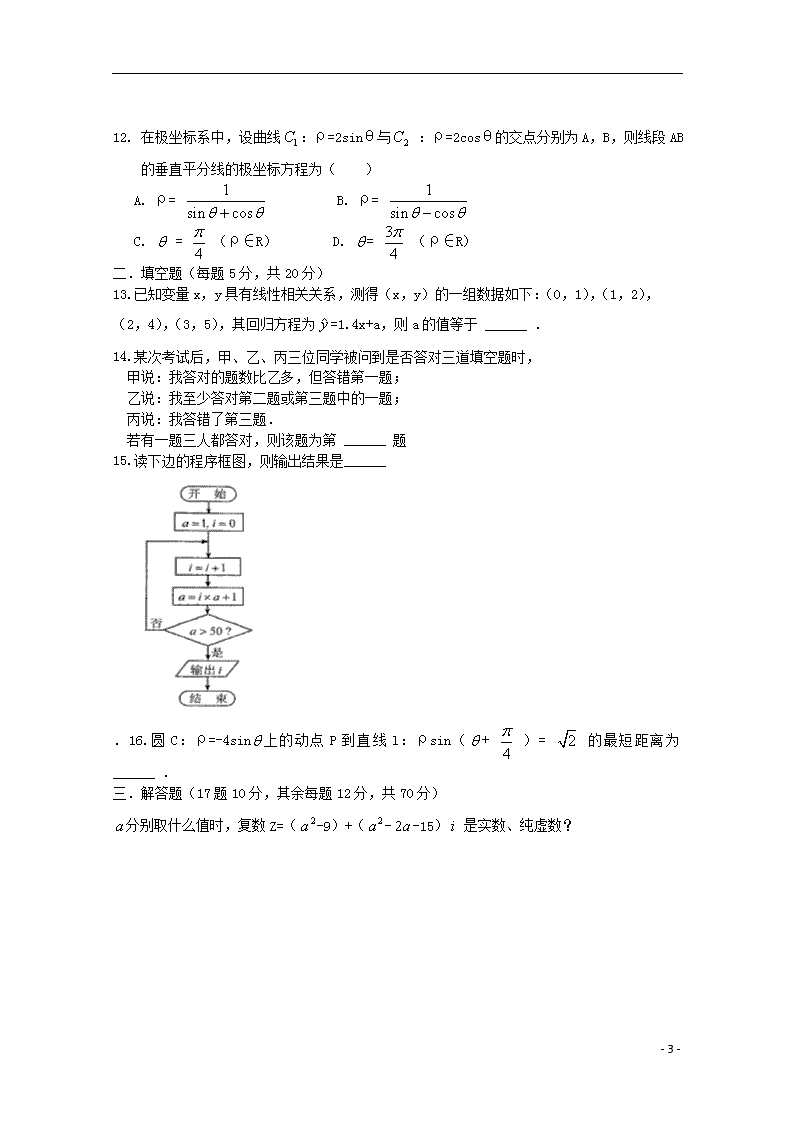12.在极坐标系中，设曲线：ρ=2sinθ与：ρ=2cosθ的交点分别为A，B，则线段AB的垂直平分线的极坐标方程为（　　）A.ρ=B.ρ=C.=（ρ∈R）D.=（ρ∈R）二．填空题（每题5分，共20分）13.已知变量x，y具有线性相关关系，测得（x，y）的一组数据如下：（0，1），（1，2），（2，4），（3，5），其回归方程为=1.4x+a，则a的值等于______．14.某次考试后，甲、乙、丙三位同学被问到是否答对三道填空题时，甲说：我答对的题数比乙多，但答错第一题；乙说：我至少答对第二题或第三题中的一题；丙说：我答错了第三题．若有一题三人都答对，则该题为第______题15.读下边的程序框图，则输出结果是______．16.圆C：ρ=-4sin上的动点P到直线l：ρsin（+）=的最短距离为______．三．解答题（17题10分，其余每题12分，共70分）分别取什么值时，复数Z=（-9）+（--15）是实数、纯虚数？-9- =经过伸缩变换的曲线方程是什么？19.已知n≥0，试用分析法证明：——．20.某种产品的广告费用支出x（万元）与销售额y（万元）之间有如下的对应数据x24568y3040605070（1）求回归直线方程；（2）据此估计广告费用为12万元时的销售额约为多少？参考公式：=,21.某班主任对全班50名学生进行了作业量多少的调查，数据如下：认为作业多认为作业不多总计喜欢玩手机18927不喜欢玩手机71623总计252550则认为喜欢玩手机与认为作业多少有关系的把握大约为多少？（附：参考公式：,其中n=a+b+c+d．）临界值表：P()K22.在极坐标系中，已知直线l:ρsin（+）=2与圆O：ρ=4．（1）分别求出直线l与圆O对应的直角坐标系中的方程；（2）求直线l被圆O所截得的弦长．-9- 文科数学试题答案1.【答案】D【解析】知识点：复数的运算解：∵（1+2i）z=1，∴（1-2i）（1+2i）z=1-2i，∴5z=1-2i，∴z=． ∴复数z对应点坐标为位于第四象限． 故选：D． 2.【答案】D【解析】知识点：极坐标与直角坐标的互化解：点M的直角坐标（，-1） 由x=ρcosθ，y=ρsinθ， ∴=ρcosθ，-1=ρsinθ， 解得：ρ=2，θ=， ∴极坐标为（2，） 故选D． 3.【答案】C【解析】知识点：演绎推理解：用三段论形式推导一个结论成立， 大前提应该是结论成立的依据， ∵由无理数都是无限不循环小数 e是无限不循环小数，所以e是无理数， ∴大前提是无理数都是无限不循环小数． 故选C． 4.【答案】D【解析】知识点：回归直线方程解：由于线性回归方程中x的系数为0.85，因此y与x具有正的线性相关关系，A正确； 由线性回归方程必过样本中心点，因此B正确； 由线性回归方程中系数的意义知，x每增加1cm，其体重约增加，C正确； 当某女生的身高为160cm时，其体重估计值是，而不是具体值，因此D错误． 故选：D． 5.【答案】B【解析】知识点：复数的运算-9- 解：i+i2+i3+…+i2017=． 故选：B． 6.【答案】A【解析】知识点：极坐标方程与直角坐标方程的互化解：∵圆ρ=4cosθ，∴ρ2=4ρcosθ．，化为普通方程为x2+y2=4x，即（x-2）2+y2=4，∴圆心的坐标为（2，0）． ∵直线（ρ∈R），∴直线的方程为y=x，即x-y=0． ∴圆心（2，0）到直线x-y=0的距离=． 故选A． 7.【答案】B【解析】知识点：极坐标方程与直角坐标方程的互化解：极坐标方程ρ=sinθ+cosθ，即ρ2=ρ（sinθ+cosθ）， 化为x2+y2=x+y，配方为：=， 表示的曲线是以为圆心，为半径的圆． 故选：B． 8.【答案】B【解析】知识点：可线性化的回归分析解：用系数R2的值判断模型的拟合效果，R2越大，模型的拟合效果越好，故（1）正确， 可用残差平方和判断模型的拟合效果，残差平方和越小，模型的拟合效果越好，故（2）不正确 可用相关系数r的值判断两个变量的相关性，|r|越大，说明相关性越强，故（3）不正确， 残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高，故（4）正确， 综上可知有2个命题正确， 故选B．9.【答案】A【解析】知识点：合情推理解：观察数列{an} 中，a1=1，a2=3+5，a3=7+9+11，a4=13+15+17+19，…， 各组和式的第一个数为：1，3，7，13，… 即1，1+2，1+2+2×2，1+2+2×2+2×3，…， 其第n项为：1+2+2×2+2×3+…+2×（n-1）． ∴第10项为：1+2+2×2+2×3+…+2×9=1+2×=91． 从而a10的第一个加数为91． 故选A． 10.【答案】C知-9- 【解析】识点：独立性检验的应用解：若K2的观测值为k.635，我们有99%的把认吸烟与患肺病有关系；而不是在1个烟的必有9患有肺病， 若从统计量中求95%的握为吸烟与患肺病有关系，是指5可能性得推判出现错误，；故选C．  11.【答案】C【解析】知识点：线性化的回归分析解：比较两个模型的拟合效果时，如果模型残差平方和越小， 则相应的相关指数R2越大，该模型拟合的效果越好． 故选C． 12.【答案】A【解析】知识点：极坐标解：∵曲线C1：ρ=2sinθ，∴ρ2=2ρsinθ， ∴曲线C1的直角坐标方程为x2+y2=2y， ∵C2：ρ=2cosθ，∴ρ2=2ρcosθ， ∴C2的直角坐标方程为x2+y2=2x， 联立，得，或， ∴线段AB的垂直平分线的斜率k=-1，AB的中点为（，）， ∴线段AB的垂直平分线的方程为：y-=-（x-），即x+y-1=0． ∴线段AB的垂直平分线极坐标方程为ρsinθ+ρcosθ=1，即． 故选：A． 13.【解析】知识点：回归直线方程解：∵==1.5，==3， ∴这组数据的样本中心点是（1.5，3） 把样本中心点代入回归直线方程， ∴3=1.4×1.5+a， ∴a=0.9． 故答案为：0.9． 14.【答案】二【解析】知识点：合情推理解：由题意如表格： 第一题第二题第三题甲×（已知）√√乙×√√（或×）丙√√×（已知）-9- 第一题和第三题 都有人错，那只能是第二题 全对． 故答案为：二． 15.【答案】4【解析】知识点：程序框图16.【答案】2-2【解析】知识点：圆的极坐标方程解：圆C：ρ=-4sinθ，即ρ2=4ρsinθ，化为x2+y2=-4y，配方为x2+（y+2）2=4，可得圆心C（0，-2），半径r=2． 到直线l：ρsin（θ+）=化为=，化为x+y-2=0． ∴圆心C到直线l的距离d==2， ∴圆C上的动点P到直线l的最短距离=d-r=2-2． 故答案为：2-2．17.【解析】知识点：复数解：由题可知： （1）当a2-2a-15=0时，复数Z=（a2-9）+（a2-2a-15）i是实数， 即a=5或a=-3时，复数Z=（a2-9）+（a2-2a-15）i是实数；，  （2）当时，复数Z=（a2-9）+（a2-2a-15）i是纯虚数， 即a=3时，复数Z=（a2-9）+（a2-2a-15）i是纯虚数．18.【解析】知识点：坐标的伸缩变换y2=16/9x19.【解析】知识点：分析法证明：要证上式成立，需证，只需证， 只需证，只需证(n+1)2＞n2+2n，需证n2+2n+1＞n2+2n，只需证1＞0． 因为1＞0显然成立，所以，要证的不等式成立．20.【解析】知识点：回归直线方程-9- 解：（1）求回归直线方程==5==50 b=  ∴因此回归直线方程为y=6.5x+17.5； （2）当x=12时，预报y的值为y=12×6.5+17.5=95.5万元．  21. 【答案】9%【解析】知识点：独立性检验的应用解：由表中数据可知x2=≈6.522＞， ∴有9%的把握判定变量A，B有关． 故答案为：97.5%． ∴直线l与圆C相离．22.【解析】知识点：圆与直线的极坐标方程解：（1）∵ρsin（θ+）=2， ∴ρsinθ+ρcosθ=2， ∵ρcosθ=x，ρsinθ=y， ∴化成直角坐标方程为：x+y-2=0， 圆ρ=4化成直角坐标方程为x2+y2=16， （2）圆心到直线的距离为：d==2， ∴截得的弦长为：2=4．-9-