达朗贝尔原理课件.ppt 44页

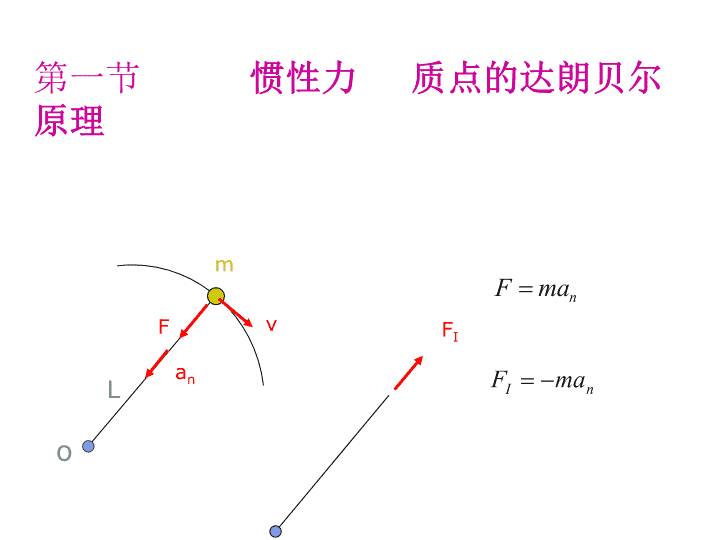
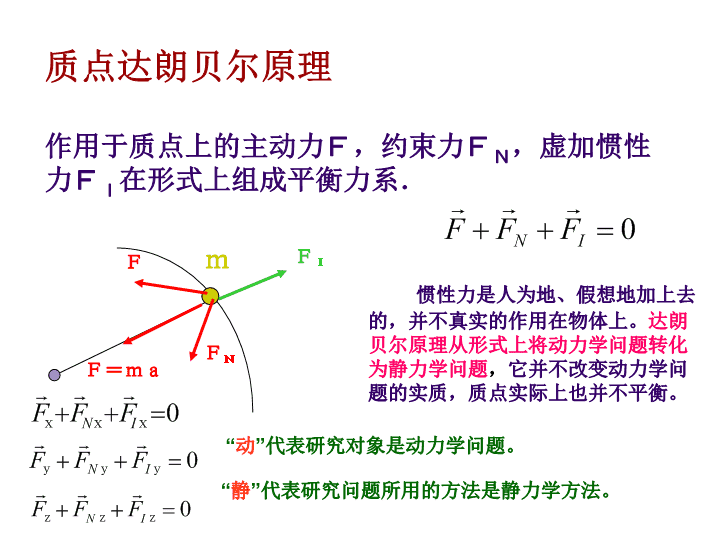
达朗贝尔原理动静法:用静力学中研究平衡问题的方法来研究动力学问题. oLmFvanFI第一节惯性力质点的达朗贝尔原理 质点达朗贝尔原理作用于质点上的主动力Ｆ，约束力ＦＮ，虚加惯性力ＦＩ在形式上组成平衡力系．ｍＦＦＮＦ＝ｍａＦＩ惯性力是人为地、假想地加上去的，并不真实的作用在物体上。达朗贝尔原理从形式上将动力学问题转化为静力学问题，它并不改变动力学问题的实质，质点实际上也并不平衡。“动”代表研究对象是动力学问题。“静”代表研究问题所用的方法是静力学方法。 1、分析质点所受的主动力和约束力；2、分析质点的运动，确定加速度；3、在质点上加上与加速度方向相反的惯性力。4、用静平衡方程求解动静法的解题过程： 第二节质点系的达朗贝尔原理质点系达朗贝尔原理质点系中每个质点上作用的主动力,约束力和它的惯性力在形式上组成平衡力系.对于每个质点 ABCcbha汽车连同货物的总质量是m，其质心C离前后轮的水平距离分别是b和c，离地面的高度是h。当汽车以加速度a沿水平道路行驶时，求地面给前、后轮的铅直反力。轮子的质量不计。例题1第14章达朗贝尔原理FBmgFNAFNBFI C刚体作平动刚体作定轴转动1.转轴不通过质心,但刚体作匀速转动第三节刚体惯性力系的简化 2.转轴通过质心,但刚体作变速转动3.刚体转轴通过质心并作匀速转动刚体的惯性力系自行平衡 刚体作平面运动 OABr如图所示，滑轮的半径为r，质量为m均匀分布在轮缘上，可绕水平轴转动。轮缘上跨过的软绳的两端各挂质量为m1和m2的重物,且m1>m2。绳的重量不计，绳与滑轮之间无相对滑动，轴承摩擦忽略不计。求重物的加速度。例题2第14章达朗贝尔原理aam1gmgm2gFN 力学小魔术一根重为F的均质杆简支于A,B支座上，支座的反力分别为F/2。如果突然将支座B撤去，显然在重力矩作用下AB杆将绕A点顺时针转动而掉下。现在，允许在AB杆上采取一些措施，但不能对系统施加绕A点的外力矩，使得在支座B撤去后，AB杆仍能维持水平而不掉下。你能做到吗？ 图为一电动卷扬机构的示意图。已知起动时电动机的平均驱动力矩为M，被提升重物的质量为m1，鼓轮质量为m2，半径为r，它对中心的回转半径为ρO。试求起动时重物的平均加速度a和此时轴承O的动约束力。xyαMrm1gaOm2g例题3第14章达朗贝尔原理FIFOxFOyMI 例题3例题第14章达朗贝尔原理 重为FP的重物A沿一光滑斜面滑下，借无重而不可伸长的软绳带动重为FP1，半径为r的鼓轮转动。求鼓轮的角加速度.斜面的倾角为α，鼓轮可视为均质圆柱。滑轮C的质量和轴承摩擦可忽略不计。例题4第14章达朗贝尔原理 重为FP的重物A沿一光滑斜面滑下，借无重而不可伸长的软绳带动重为FP1，半径为r的鼓轮转动。求鼓轮的角加速度.斜面的倾角为α，鼓轮可视为均质圆柱。滑轮C的质量和轴承摩擦可忽略不计。例题4第14章达朗贝尔原理 重为FP的重物A沿一光滑斜面滑下，借无重而不可伸长的软绳带动重为FP1，半径为r的鼓轮转动。求鼓轮的角加速度.斜面的倾角为α，鼓轮可视为均质圆柱。滑轮C的质量和轴承摩擦可忽略不计。例题4第14章达朗贝尔原理设重物下滑距离为SS=rφφ——圆柱转过的角度两边对时间求一次导数 滚子A，重Q，沿倾角为α的斜面滚动而不滑动，滑轮B与滚子A有相同的质量和半径，且均可看作均值圆盘。物体C重FP，求滚子中心的加速度。设绳子不可伸长，其重量可略而不计，绳与滑轮间无滑动。例题5第14章达朗贝尔原理 滚子A，重Q，沿倾角为α的斜面滚动而不滑动，滑轮B与滚子A有相同的质量和半径，且均可看作均值圆盘。物体C重FP，求滚子中心的加速度。设绳子不可伸长，其重量可略而不计，绳与滑轮间无滑动。例题5第14章达朗贝尔原理两边对时间求一次导数 滚子A，重Q，沿倾角为α的斜面滚动而不滑动，滑轮B与滚子A有相同的质量和半径，且均可看作均值圆盘。物体C重FP，求滚子中心的加速度。设绳子不可伸长，其重量可略而不计，绳与滑轮间无滑动。例题5第14章达朗贝尔原理 飞球调速器的主轴O1y1以匀角速度w转动。试求调速器两臂的张角a。设重锤C的质量为m1，飞球A，B的质量各为m2，各杆长均为l，杆重可以忽略不计。例题4第14章达朗贝尔原理 例题4例题第14章达朗贝尔原理 球磨机是一种破碎机械，在鼓室中装进物料和钢球，如图所示。当鼓室绕水平轴转动时，钢球被鼓室携带到一定高度，此后脱离壳壁而沿抛物线轨迹落下，最后与物料碰撞以达到破碎的目的。如已知鼓室的转速为nrpm，直径为D。设钢球与壳壁间无滑动，试求最外层钢球的脱离角α。ωα例题5第14章达朗贝尔原理mgFNFFI 如图所示一圆锥摆。质量m=0.1kg的小球系于长l=0.3m的绳上，绳的一端系在固定点O，并与铅直线成θ=60º角。如小球在水平面内作匀速圆周运动，求小球的速度v与绳的张力F的大小。Olθ例题6例题第14章达朗贝尔原理 均质圆柱体A和B的重量均为P，半径均为r，一绳绕于可绕固定轴O转动的圆柱体A上，绳的另一端绕在圆柱B上，求B下落的质心的加速度，摩擦不计。例题第14章达朗贝尔原理acacatc 滚子A，重Q，沿倾角为α的斜面滚动而不滑动，滑轮B与滚子A有相同的质量和半径，且均可看作均质圆盘，物体C重P，求滚子中心的加速度，设绳子不可伸长，其重量可略而不计，绳与滑轮间无滑动。例题第14章达朗贝尔原理aaNFAIMAIMBIFCI 例题6例题第14章达朗贝尔原理 解：OlθenetebmgFF*例题6例题第14章达朗贝尔原理 OlθenetebmgFF*例题6例题第14章达朗贝尔原理 半径为R，重量为W1的大圆轮，由绳索牵引，在重量为W2的重物A的作用下，在水平地面上作纯滚动，系统中的小圆轮重量忽略不计。求大圆轮与地面之间的滑动摩擦力。AOCW1W2R例题7例题第14章达朗贝尔原理 例题7例题第14章达朗贝尔原理 解：AOCW1W2RFFNFOxFOy例题7例题第14章达朗贝尔原理 AOCW1W2RFFNFOxFOy例题7例题第14章达朗贝尔原理 CFFNJCαW1aFOxAOCW1W2RFFNFOy例题7例题第14章达朗贝尔原理 起重装置由匀质鼓轮D（半径为R，重为W1）及均质梁AB（长l=4R，重W2=W1）组成，鼓轮通过电机C（质量不计）安装在梁的中点，被提升的重物E重。电机通电后的驱动力矩为M，求重物E上升的加速度a及支座A，B的约束力FNA及FNB。OABACDE例题8例题第14章达朗贝尔原理 解：O(b)WMODEW1(b)FOxFOyα例题8达朗贝尔原理例题 OAB(b)WW2FNAACDEFNBW1(c)FxM*F*例题8例题第14章达朗贝尔原理 用长l的两根绳子AO和BO把长l，质量是m的匀质细杆悬在点O(图a)。当杆静止时，突然剪断绳子BO，试求刚剪断瞬时另一绳子AO的拉力。OlllBAC（a）例题9例题第14章达朗贝尔原理 例题9例题第14章达朗贝尔原理 解：aA=anA+atA=aCx+aCy+atAC+anACOllBACmgFθ（b）OxyαBACθ（c）例题9例题第14章达朗贝尔原理 anAC=AC·ω2=0atAC=lα／2例题5-7（b）（c）OxyαBACθOllBACmgFθ（b）（c）例题9例题第14章达朗贝尔原理 F*Cx=maCx,F*Cy=maCyM*C=JCz´αOxyαBACθOllBACmgFθxy（b）（c）例题9例题第14章达朗贝尔原理 JCz´=ml2／12（2）（3）（4）例题9OxyαBACθOllBACmgFθxy例题第14章达朗贝尔原理