内蒙古呼伦贝尔市扎兰屯一中2012-2013年度高二数学第一次综合考试 理 新人教版.doc 7页

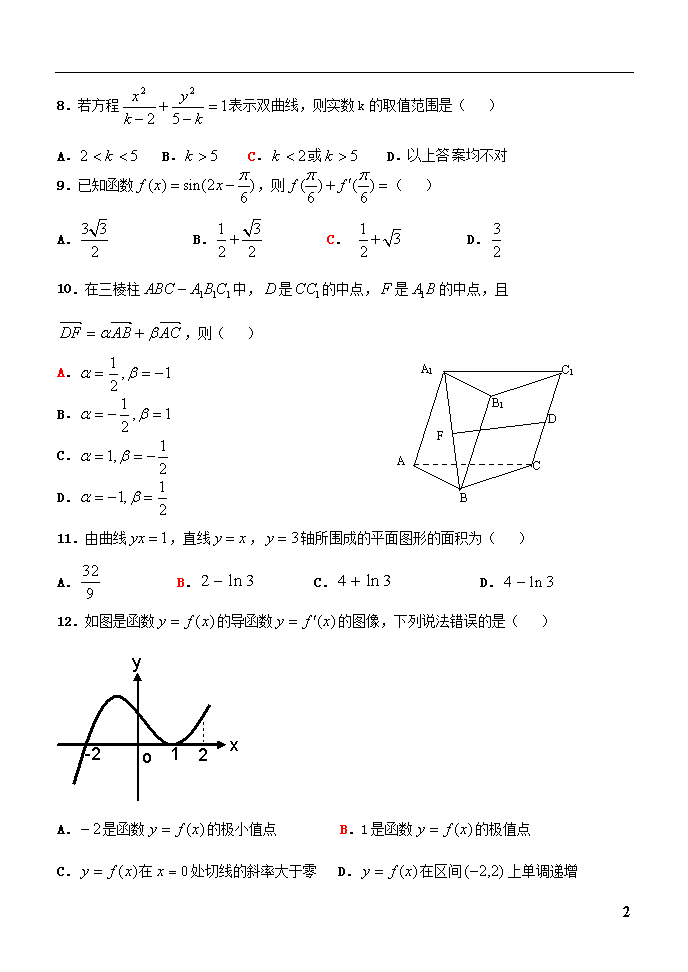
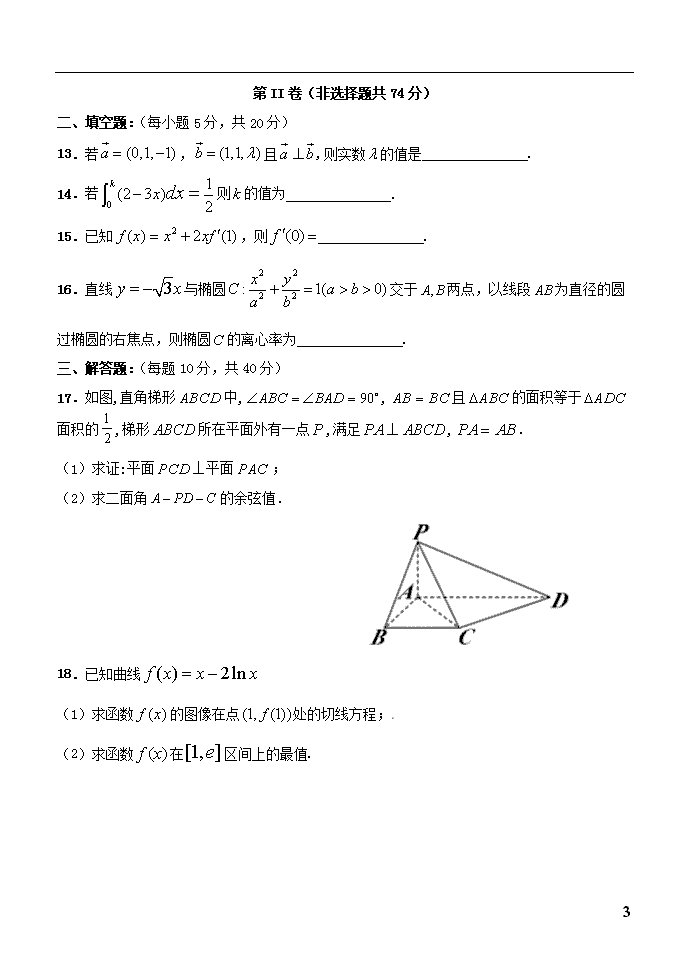
2012-2013年度扎兰屯一中高二数学第一次综合考试（新人教版）时间：100分钟总分：134分第Ⅰ卷（共60分）一、选择题：（每小题5分，每题只有一个正确答案，共60分）1．“”是“”的（）A．必要不充分条件B．充分不必要条件C．充分必要条件D．既不充分也不必要条件2．命题“若，则”以及它的逆命题，否命题和逆否命题中，真命题的个数是（）A．0B．2C．3D．43．命题“对任意的”的否定是（）A．不存在B．存在C．存在D．对任意的4．已知：且为真，则下列命题中的假命题是（）①；②或；③且；④A．①④B．①②③C．①③④D．②③④5．到定点和定直线距离相等的点的集合是（）A.双曲线B.椭圆C.抛物线D.直线6．若函数，图象上及邻近上点，则=（）A．B．C．D．7．等于（）A．-2B．2C．0D．17 8．若方程表示双曲线，则实数k的取值范围是（）A．B．C．或D．以上答案均不对9．已知函数，则（）A．B．C．D．10．在三棱柱中，是的中点，是的中点，且，则（）B1A1CBAC1DFA．B．C．D．11．由曲线，直线，轴所围成的平面图形的面积为（）A．B．C．D．12．如图是函数的导函数的图像，下列说法错误的是（）A．是函数的极小值点B．1是函数的极值点C．在处切线的斜率大于零D．在区间上单调递增7 第II卷（非选择题共74分）二、填空题：（每小题5分，共20分）13．若，且,则实数的值是.14．若则的值为.15．已知，则.16．直线与椭圆交于两点，以线段为直径的圆过椭圆的右焦点，则椭圆的离心率为.三、解答题：（每题10分，共40分）17．如图,直角梯形中,,且的面积等于面积的,梯形所在平面外有一点,满足,．（1）求证:平面⊥平面；（2）求二面角的余弦值．18．已知曲线（1）求函数的图像在点处的切线方程；（2）求函数在区间上的最值.7 19．如图所示，椭圆的离心率为，且是椭圆C的顶点。（1）求椭圆C的方程；（2）过点A作斜率为1的直线，设以椭圆C的右焦点F为抛物线的焦点，若点M为抛物线E上任意一点，求点M到直线距离的最小值.20．已知函数，其中为实数.（1）若在处取得的极值为，求的值；（2）若在区间上为减函数，且，求的取值范围.附加题：（本题可做可不做，满分14分,所得分数计入总分）设函数.（1）若，求的单调区间；（2）若当时，求的取值范围.7 （理科数学）答案一、选择题BBCCCAACCABB二、填空题11或-4三、解答题：17.（1）证明：∵PA⊥平面ABCD,∴CD⊥PA．又△ABC的面积等于△ADC面积的,∴．在底面中，因为，，所以，所以．又因为，所以平面．而CD平面PCD，∴平面PCD⊥平面……5分（2）设为中点，连结，则．又因为平面平面，所以平面．过作于，连结，由三垂线定理可知．所以是二面角的平面角．设，则,．在中，，所以．所以，．即二面角的余弦值为．……10分18.（Ⅰ）∵∴…2分∴，又，所以切点坐标为…3∴所求切线方程为，即.…………5分（Ⅱ）……6分所以存在极小值……8分所以最小值为最大值为……10分19.解：（1）由题意可知，7 ，即所以椭圆C的方程为：……5分（2）方法一：由（1）可求得椭圆C的坐标F（1，0）抛物线E的方程为：，而直线的方程为设动点M为，则点M到直线的距离为即抛物线E上的点到直线距离的最小值为……10分方法二：由（1）可求得椭圆C的右焦点坐标F（1，0）抛物线E的方程为：，而直线的方程为可设与直线平行且抛物线E相切的直线方程为：由可得：9分，解得：直线方程为：抛物线上的点到直线的距离的最小值等于直线与的距离：20.解(Ⅰ)由题设可知:且，………………2分即，解得………………5分（Ⅱ），………………6分7 又在上为减函数，对恒成立，………………7分即对恒成立.且，………………8分即，的取值范围是………………10分附加题：（1）时，，.当时，；当时，.故在单调减少，在单调增加（II）由（I）知，当且仅当时等号成立.故，从而当，即时，，而，于是当时，.由可得.从而当时，，故当时，，而，于是当时，.综合得的取值范围为.7