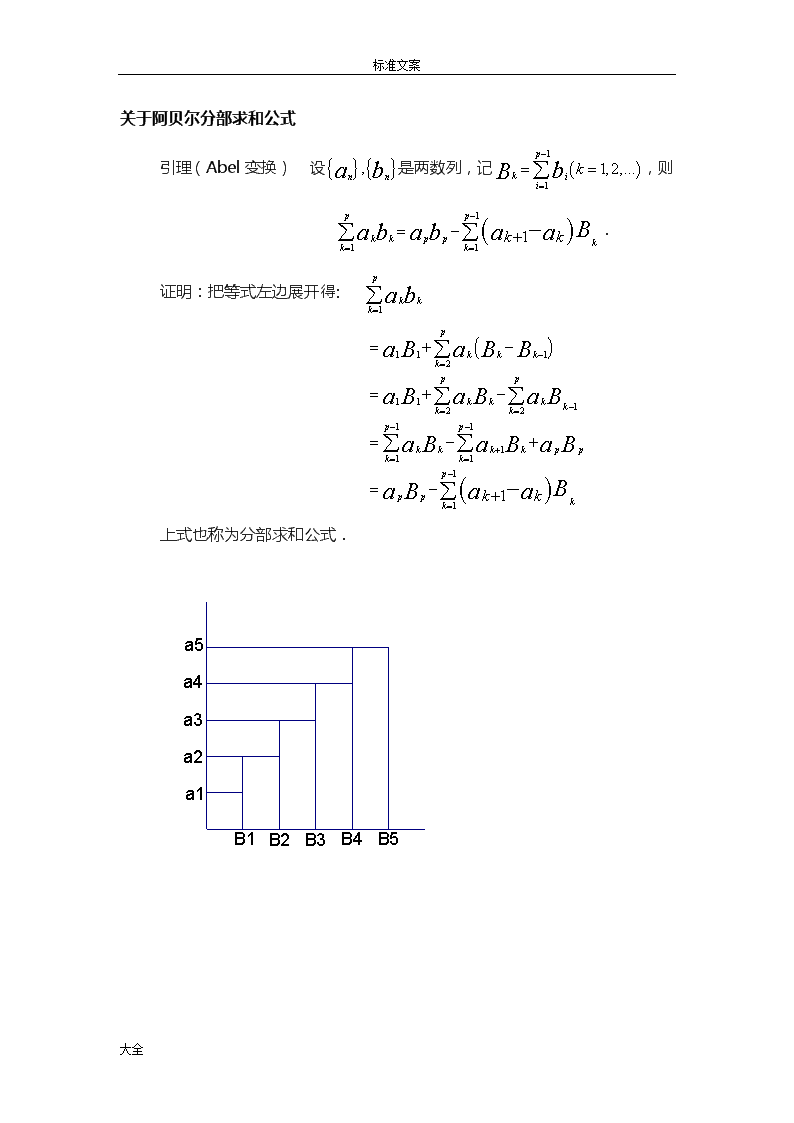阿贝尔分部求和公式地推广及应用 11页

标准文案关于阿贝尔分部求和公式引理（Abel变换）　设是两数列，记，则　　　　　　　　　　　．证明：把等式左边展开得:　　　　　　　　　　　　　　　　上式也称为分部求和公式．　　大全 标准文案上图是当，且单调增加时，Abel变换的直观的示意．图中矩形被分割成9个小矩形，根据所标出的各个小矩形的面积，即得到p=5的Abel变换：　　　　　　　　事实上，Abel变换就是离散形式的分部积分公式．记则分部积分公式可以写成　　　　　　　　　．将数列的通项类比于函数，求和类比于求积分，求差类比于求微分，　－对应于，则两者是一致的．　　　　　　　　　　　三　阿贝耳分部求和公式的推广及应用（一）关于数论方面的推广和应用定理1　设，是一个数论函数，　　　　　　　　　　　　　．再设是区间上的连续可微函数，那么有　　　　　＝＿＿．证明：设＝，＝．我们有（约定＝0）=大全 标准文案==－＿+=－＝－＋此外还有　　　　＝　　　　注意到＝，＝，由以上三式即得公式成立．　　由阿贝耳求和公式可知，如果我们知道了数论函数的均值的渐进公式，那么，对于满足适当条件的函数，数论函数的均值的渐进公式有可能通过定理公式得到。（二）关于阿贝耳引理及其推广和应用1．关于级数收敛性问题定理2(Abel引理)　　设（1）为单调数列；（2）为有界数列，即存在M>0,对一切k，成立，则大全 标准文案　　　　．证明：由Abel变换可得，　　　　由于单调，所以　　　　＝．　　　　定理1　（级数的Abel判别法）单调有界，收敛，则级数敛．证明：设，由于收敛，则对于任意给定的＞0，存在正整数N，使　得对于一切n>N和p,成立　　　　　　　　　　　　　　　＜.　　　对于应用Abel引理，即得　　　　　　＜3M.定理　2（阿贝耳定理）　设＝s,则＝s.证明：容易看出＝在大全 标准文案上为一致收敛．事实上，对任给正数，有N使得当n>N时＜．从而由阿贝耳引理可知同时有＜，只要．因此由函数数项级数的连续性定理可得　　　　　　　　　　　　　　　　　　　　　＝＝s.定理2(级数乘法原理)　令．又设级数都收敛．则　　　　　　　　　　　　　　　　．证明：因为绝对收敛的级数可以相乘，因此　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　＝　（）　　　　　　　　　　　　　　于是由阿贝耳定理便可得到　　　　　　　＝＝　　　　　　　　　　＝＝．例题1试证　证明：应用阿贝耳关于级数乘法的定理，取＝＝（n=1,2,3,…）,==0,则有　　　　　　＝．．．＋＝，此处大全 标准文案　　　　　　　＝显然有　　　n=(1+)+(2+)+…+(+1)=2(1++…+)＝2ln＋2+o(1)()其中为欧拉常数．于是．又因为（n+1）－＝　　　　　　（－）＝－［（n+1）－n］=－>0　故得　　　　　．　从而由莱布尼兹收敛判别法可见级数＝是收敛的，　最后由级数乘法原理可知该命题是成立的．　例题2设．试证二重级数　　　　　　　　　　　　　　　　　　　　　为收敛的．　分析：不难看出　　　　　以及　　　　　　　　－＝，大全 标准文案　　　　　　－－＋　　　　　　　　　　　　　　　=，其中＝（当m+n时）．2．关于级数求和问题　例题1　=ln2.证明:当时，可得＝ln(1+x)故得　＝ln(1+x)＝ln2.例题2设求证　　　　　　　　　　　＝　证明：显然左端的级数是收敛的，把它写成　　　　　　　　　＝，而作函数　　　　＝　　　（）从而　　　　＝＝（）．大全 标准文案由于＝0,故　　　　＝　　　　　（）因此，　应用定理便可得到要证明的等式．　　　　　　　　　　　（三）关于连续变量的阿贝耳分部求和公式及其应用　　　当下标n变成连续变量时，与和差变换相应的是分部积分公式，与阿贝耳引理相应的是鲍纳的积分中值定理．我们已经熟悉掌握了黎曼积分的初步知识，所以这里可以把一些命题变成较一般的形式．　定理1（分部积分法）设黎曼积分存在，则也存在，并且有分部积分公式　　　　　＝－．证明：以表示［a,b］的任意划分：　　　　　：a==b,并记＝max()（）.应用和差变换于积分和　　　　　　　，其中计值点组　适合　（k=1,2,…,n）,我们得到　　　大全 标准文案　　　　　　　＝　　　　　　　＝，　　其中为划分，　　　而计值点组＝，　　　于是为积分的积分和，并且＝max()()所以令时，便得　＝　　　　　　　＝－＋　　注意：若连续而为有界变差的函数，则积分存在．而由本命题可知，当为连续而为有界变差时，积分也存在．　定理2　（第一中值定理）设为一单调函数而为实值连续函数，则有中值公式＝　　　（）．提示：此命题的证法与通常黎曼积分的中值公式证法相似．　定理3　（第二中值定理）设在［a,b］上为一实值连续函数而为一单调函数．则必有，使得　　　　　　＝＋．　提示：应用分部积分公式后再应用第一中值定理即得．例题1设和满足大全 标准文案　　　　　　　　　　　　　　　．又设为非增函数，则　　　　　　证明：令G(t)=,则G(x)0.G(a)=G(b)=0,所以有　　　－＝G(t)　　　＝－　　　＝－　．例题2不等式（1）（式中）对每一个不增的函数都成立的充分必要条件是函数对所有满足　　　　　　　且(2)成立．证明：必要性：　　　设，则不等式(1)给出（），（3）0(),(4)设，则有(4)得　　=+.设，则有（3）得　　　＝－－（）＝＋－所以（3）和(4)对所有的都成立．同样可证　　　　　　　　，大全 标准文案对于所有的成立．所以当不等式（1）对所有的不增的成立时不等式(2)成立．　　　充分性：　　　由已知可得－＝＋　利用分部积分公式　　　　　容易看出当（2）式成立时　　　　＝　　　　＝　所以（1）右边的不等式成立．　同样的道理可以证明左边的不等式也成立．大全