达朗贝尔原理动静法1 18页

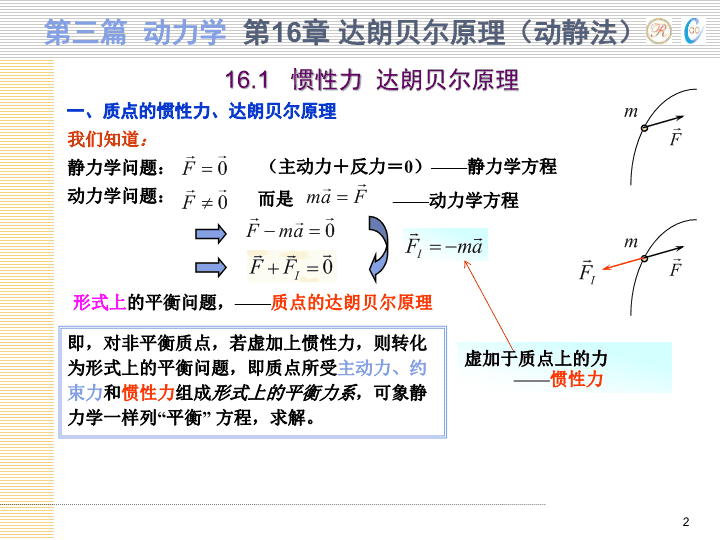
第三篇动力学第16章达朗贝尔原理（动静法）每当讲到达朗贝尔原理，总有一种痛快的感觉——终于可以抛弃那些烦人的概念和定理，什么动能、动量啊，各种各样的定理、守恒定律啊。感谢法国科学家达朗贝尔吧！三大定理可解决所有动力学问题，但有些问题的求解并不方便，如多刚体动力学（如机器人——物体多但自由度较少），而用分析力学的方法则较方便。分析力学的基础则是：达朗贝尔原理——用静力学方法解决动力学问题虚位移原理——用动力学方法解决静力学问题达朗贝尔原理（动静法）特点：简单、新颖、实用，只用一个概念（惯性力）、一个理论（达朗贝尔原理），而不用前面三大定理中诸多概念（动能、动量、动量矩、功、冲量等）。1 16.1惯性力达朗贝尔原理一、质点的惯性力、达朗贝尔原理静力学问题：（主动力＋反力＝0）——静力学方程动力学问题：而是形式上的平衡问题，——质点的达朗贝尔原理即，对非平衡质点，若虚加上惯性力，则转化为形式上的平衡问题，即质点所受主动力、约束力和惯性力组成形式上的平衡力系，可象静力学一样列“平衡”方程，求解。我们知道：——动力学方程虚加于质点上的力——惯性力第三篇动力学第16章达朗贝尔原理（动静法）2 给所研究的质点系加上惯性力系后，则转化为形式上的平衡问题，可列任意平衡方程求解。——质点系的达朗贝尔原理问题：惯性力系（主要是刚体）如何简化？即对质点系整体如何加惯性力？二、质点系的惯性力、达朗贝尔原理质点系每个质点的惯性力：然而，不可能对每个质点加惯性力，需进行简化，特别是对刚体。组成一惯性力系16.2刚体惯性力系的简化一、平动刚体向质心简化：主矢：主矩：惯性力系：——惯性力——惯性力偶所以，平动刚体惯性力只有作用在质心上的惯性力，大小等于MaC，方向与aC相反。即C第三篇动力学第16章达朗贝尔原理（动静法）3 二、转动刚体只讨论平面情形，即绕垂直于质量对称面之轴O的转动刚体。任一质点：惯性力系：方法1：向轴O点简化主矢：主矩：方法2：向质心C简化即——惯性力——惯性力偶即主矢——惯性力：完全同上。主矩：即转动刚体惯性力有两种加法：①在轴上加惯性力，在刚体上加惯性力偶；②在质心上加惯性力，在刚体上加惯性力偶。注意：作用于轴O注意：作用于质心C简化中心如何取？COCO为什么？第三篇动力学第16章达朗贝尔原理（动静法）4 C三、平面运动刚体动系：随质心平动。任一质点：惯性力系：主矢：主矩：向质心C简化：——惯性力——惯性力偶所以，平面运动刚体惯性力是：作用在质心上的惯性力和作用在刚体上的惯性力偶。即即0第三篇动力学第16章达朗贝尔原理（动静法）5 特别注意：关于上述诸式中惯性力和惯性力偶“－”号的处理：画图时——总是按照质心加速度和刚体角加速度相反方向画出惯性力与惯性力偶；写公式时——总是只写惯性力与惯性力偶的大小表达式。如：图中画出惯性力和惯性力偶，而其表达式为：解题步骤：（一）取分离体；（三）列解“平衡”方程。（二）画受力图（主动力、约束力、惯性力（偶））；只有此处是新的！问题：达朗贝尔原理（动静法）能求解何种量？第三篇动力学第16章达朗贝尔原理（动静法）6 例1（例12-1改，用达朗贝尔原理求解）图示系统。均质滚子A、滑轮B重量和半径均为Q和r，滚子纯滚动，三角块固定不动，倾角为，重量为G，重物重量P。求滚子运动到斜面中部时，质心C的加速度和地面给三角块的反力。设三较块底边长b，斜面长L。PQQCOAB分析：先考虑求aC。惯性力中包含aC。研究对象如何取？先尽量不拆开物系。考虑整体，包含地面反力，故不能求aC。考虑重物、轮子和滚子组成的物系，加惯性力后受力如图。PQQaaCεCOABεE考虑各惯性力和惯性力偶中的加速度和角加速度可以统一，N可以在力矩方程中消去，对O列力矩“平衡”方程，可求aC：所有惯性力和惯性力偶均已知，对整体列“平衡”方程，可求出地面反力。第三篇动力学第16章达朗贝尔原理（动静法）7 解：I.求加速度aC。研究重物、轮子、滚子整体，画受力图如图。其中惯性力和惯性力偶大小：PQQaaCεCOABεE且QaCεCAE(1)(2)考虑滚子受力，列斜面法向平衡方程：(3)将(1)、(3)式代入方程(2)，可求得：第三篇动力学第16章达朗贝尔原理（动静法）8 II.求地面反力。研究整体，画受力图如图。PQOBYHXHmHεQaCεCAEDHa(4)(5)(6)将前面结果代入以上三式，解得第三篇动力学第16章达朗贝尔原理（动静法）9 例2（例14-11，刚体平面运动微分方程。现用动静法求解）还记得前面如何求解的吗？注：由此题可知，达朗贝尔原理与动量定理和动量矩定理等效。故要求用达朗贝尔原理求解问题时，不能用此二定理，但可用动能定理。均质杆AB，质量m，长l。在图示位置释放。求此时杆的角加速度。30°45°ABC解：画杆受力、运动图，如图。回顾一下。刚体平面运动微分方程：aCxaCy30°45°ABCmgNATB第三篇动力学第16章达朗贝尔原理（动静法）10 (1)(2)(3)选A为基点，C为动点，画加速度图如图。在水平方向上投影：在铅直方向上投影：(4)(5)3个方程，5个未知量至此，共5个方程，6个未知量BaCxaCy30°45°ACmgNATB第三篇动力学第16章达朗贝尔原理（动静法）11 选A为基点，B为动点，画加速度图如图。在铅直方向上投影：(6)共6个方程，6个未知量联立方程(1)~(6)，得BaCxaCy30°45°ACmgNATB此题共写出3个动力学方程，3个运动学方程，求解还是较繁的。第三篇动力学第16章达朗贝尔原理（动静法）12 BaCxaCy30°45°ACmgNATB现考虑用动静法求解。解：画杆受力、运动图，如图。其中惯性力和惯性力偶：FIxFIyMIC(a)考虑列“平衡”方程。由于NA，TB不要求，故列方程时尽量避开。为沿斜面方向投影轴，如图。可以吗？(1)(2)考虑(a)式，(1)(2)方程包含4个未知量：aCx，aCy，，TB。第三篇动力学第16章达朗贝尔原理（动静法）13 选A为基点，C为动点，画加速度图如图。在NA方向投影：在铅直方向上投影：(3)(4)至此，共4个方程，4个未知量BaCxaCy30°45°ACmgNAεTB考虑刚才的处理方式，列上式投影方程时避开aA，即在NA方向投影。式中BaCxaCy30°45°ACmgNAεTB选B为基点，C为动点，画加速度图如图。式中第三篇动力学第16章达朗贝尔原理（动静法）14 注1：应用达朗贝尔原理列力矩平衡方程时，矩心可任意选，但动量矩定理中矩心不能任意选。所以由动静法写出2个动力学方程——比用平面运动微分方程少写1个方程；问题：既然达朗贝尔原理如此好用，是否可不讲三大定理而只讲此原理呢？在求解众多动力学问题中，达朗贝尔原理是好用的。但由于其所用物理概念很少，故定性解释某些问题时受到的局限性也较大，如能量转换、碰撞问题等。三大定理建立了很多概念，故能定性解释许多问题。联立方程(1)~(4)，解得注2：在补充运动方程时，用到一些技巧，避开了中间未知量aA、aB，只写出2个运动学代数方程。第三篇动力学第16章达朗贝尔原理（动静法）15 例3（例16-8）（转子动反力）——动静法重要应用）水平转子m=300kg，回转半径=0.2m，偏心距e=2mm，圆盘位置L1=0.40m，L2=0.35m，起动力矩M=150kN·m，在图示位置，转速n=2400rpm。求此时转子的角加速度和轴承动反力。L2L1ABxyzCOeMmg分析：不用动静法如何求？转子受力、运动如图。L2L1ABxyzCOeMmgXAYAXBYB第三篇动力学第16章达朗贝尔原理（动静法）16 考虑用动静法求解。解：画转子受力、运动图，其中惯性力和惯性力偶向轴上加，如图。式中列“平衡”方程，并考虑(a)式：L2L1ABxyzCOeMmgXAYAXBYB(a)MIO第三篇动力学第16章达朗贝尔原理（动静法）17 作业：16-7，16-9，16-18，16-19（较难）下次课预习：虚位移原理讨论：如果转子静止，易求得静反力：可见，由惯性力引起的附加动反力（沿径向）比静反力要大得多。所以，对旋转机械，必须要施以动平衡。则附加动反力：L2L1ABxyzCOeMmgXAYAXBYB第三篇动力学第16章达朗贝尔原理（动静法）18