2012年呼伦贝尔市初中学业考试数学学科质量分析 11页

2012年呼伦贝尔市初中毕业生学业考试数学学科质量分析呼伦贝尔市教育研修学院初中教研室一、考试命题依据和命题原则1．考试命题的依据命题以《全日制义务教育数学课程标准(实验稿)2001版》及2012年呼伦贝尔市初中毕业生学业考试数学考试说明为依据。以本届毕业生所用教材为基本命题材料，结合数学学科的教学实际进行命题。2．考试命题的原则命题坚持基础性、公平性、现实性、有效性相结合的原则。稳中求进，兼顾导向性与选拔性功能。面向全体学生，力求公正、客观、全面、准确地评价学生通过义务教育阶段数学学习，学生的数学思维、数学观念与数学素养所获得的相应发展，从而促进教学方法与学习方式的转变，促进数学课程目标的实现。二、试题质量分析(一)试题特点：试题重视基础、紧扣教材。关注对数学学科基础知识、基本技能和基本思想方法的考查。对基础知识和基本技能的考查，关注对知识本身意义的理解和在具体情境中的合理应用。大部分试题源于教材，比如解分式方程、概率题、统计题、尺规作图题、应用题等都是教材内容的挖掘、组合、改编呈现给学生，意在引导教师回归教材、重视基础、用好教材、充分挖掘教材中蕴涵的数学思想方法，改变“题海战术”的复习方式。加强了动手实践以及探索能力的考查。如尺规作图题、绘制条形统计图，重点考查学生动手实践能力；最后一道综合解答题需要学生将图形运动变化过程中部分时间段的图形独立画出来，给学生充分的自主探索的时空，考查学生的探索过程与探索方法。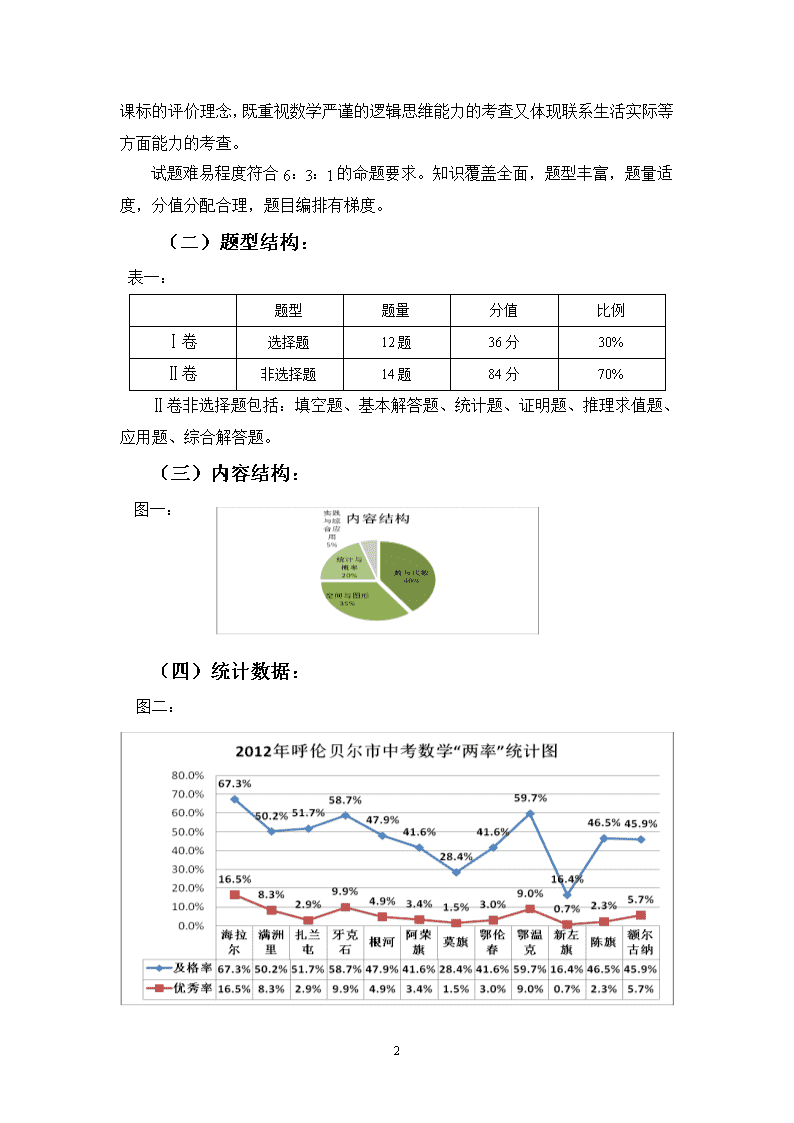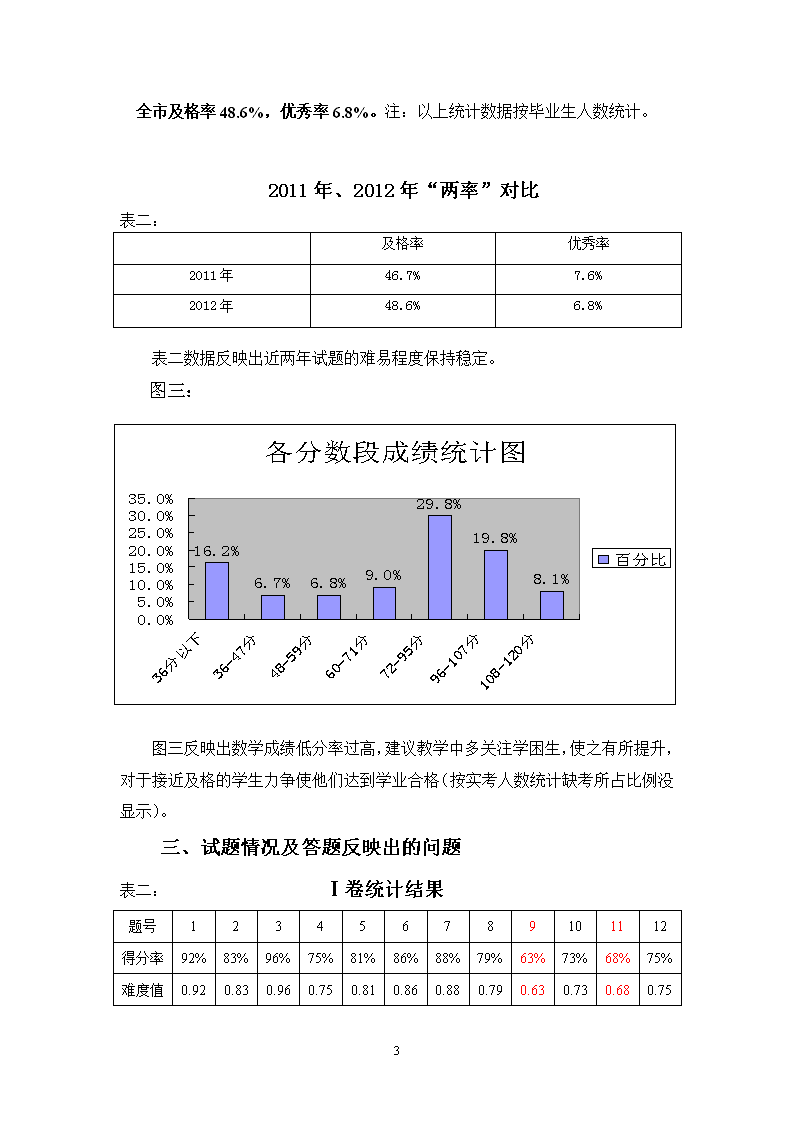为了兼顾考试的选拔功能，关注学生数学学习能力的考查，试题通过设置应用型、探究型、运动变化型等问题，多角度地考查学生解决问题的能力，11 体现新课标的评价理念，既重视数学严谨的逻辑思维能力的考查又体现联系生活实际等方面能力的考查。试题难易程度符合6：3：1的命题要求。知识覆盖全面，题型丰富，题量适度，分值分配合理，题目编排有梯度。（二）题型结构：表一：题型题量分值比例Ⅰ卷选择题12题36分30%Ⅱ卷非选择题14题84分70%Ⅱ卷非选择题包括：填空题、基本解答题、统计题、证明题、推理求值题、应用题、综合解答题。（三）内容结构：图一：（四）统计数据：图二：11 全市及格率48.6%，优秀率6.8%。注：以上统计数据按毕业生人数统计。2011年、2012年“两率”对比表二：及格率优秀率2011年46.7%7.6%2012年48.6%6.8%表二数据反映出近两年试题的难易程度保持稳定。图三：图三反映出数学成绩低分率过高，建议教学中多关注学困生，使之有所提升，对于接近及格的学生力争使他们达到学业合格（按实考人数统计缺考所占比例没显示）。三、试题情况及答题反映出的问题表二：Ⅰ卷统计结果题号123456789101112得分率92%83%96%75%81%86%88%79%63%73%68%75%难度值0.920.830.960.750.810.860.880.790.630.730.680.7511 总计Ⅰ卷：平均分28.8分，难度值0.8表二数据反映出选择题得分情况较好。表三：Ⅱ卷抽样统计结果（共抽取420份试卷）题号一二三四五六七总分分值1524778101384平均分10.915.55.764.754.273.183.3950.9难度值0.720.640.820.680.530.320.260.6由表二、表三统计数据反映出试题难度符合6：3：1的命题要求。Ⅰ卷选择题共12小题，满分36分，平均得分28.8分。本题基础性强，涉及知识面广。考查了初中数学数与代数、空间与图形、统计与概率等方面的基础知识和基本技能。整体得分情况较好，从统计结果反映出第⑷⑼⑽⑾⑿小题错误率偏高，反映出以下问题：1.第⑼小题：“在数据中，随机选取一个数，选中无理数的概率为”有37%的学生选错答案。错因：一方面是学生对无理数的概念不理解，另一方面是部分学生没有掌握求简单事件的概率的方法。2．函数问题失分率偏高。第⑷小题观察反比例函数图象，确定k值，失分率25%，主要原因是学生没有将函数图象与函数解析式联系起来，不会观察图象结合已知条件确定点B的坐标,从而求出K值。第⑽小题选择“一次函数的图象不经过的象限”，失分率27%，学生不能正确地画出函数的图象，没有理解一次函数解析式中k值、b值对于确定函数图象的位置所起到的作用，缺少数形结合的意识。3．第⑾小题求图形旋转后顶点A经过的弧长，失分率32%。错因：部分学生弧长公式记忆不准确、或计算出错、或对图形旋转的基本性质没有掌握。4．从失分率较高的题目看，基本都是涉及了两个或两个以上知识点的，如第⑿小题涉及到的知识点有相似三角形的性质及判定，失分率25%，第⑾11 小题涉及旋转的性质、勾股定理、弧长公式，失分率32%，明显反映出部分基础稍差的学生综合运用基础知识的能力欠缺。Ⅱ卷非选择题（一）填空题：共5小题，满分15分，平均得分10.9分。本题考查点有确定简单函数的自变量的取值范围、因式分解、利用求平均数的方法列方程求未知数的值、根据条件确定平面内点的坐标及规律探究，学生答卷反映出以下两方面的问题：1．第⑴小题确定函数自变量的取值范围，失分率36%。正确答案x≤5,典型错误：x＜5或x≥5、x≤5且x≠3等。错因：部分学生没有理解二次根式有意义的条件，不等式的解法掌握不好。第⑶题分解因式，失分率40%，正确答案是3（3x-1）2，典型错误：27（x-）2、3（9x2-6x+1）、结果中相同因式不写成幂的形式(不扣分)等。错因之一是知识混淆，本题涉及方法是先提公因式再用完全平方公式，相当一部分学生提取公因式不是提出各项系数的最大公约数3，而是提出的二次项的系数27，与配方法混淆导致答题出错、还有部分学生是分解不彻底，没有掌握完全平方公式的本质特征。1.第⑷小题求第二象取内点的坐标，有横坐标为正数的、横纵坐标颠倒的、还有多答案的情况。第⑸小题观察规律，确定的个位数字，失分率32%，典型错误：直接求出了的最后计算结果32768、或填写的“偶数”。错因是审题不认真或没有理解题意。（二）解答题：共4小题，满分24分，平均得分15.5分。本题含盖知识点较多，数与代数部分包含了简单的三角函数的计算、负指数、零指数幂的运算、分式方程的解法；统计与概率部分的求简单实际问题中事件发生的概率；空间与图形部分的尺规作图。各题得分情况如下（表四）：题号6789平均得分4.694.053.872.34难度值0.780.670.640.39答题存在以下问题：11 1.部分学生计算题不写“解”或直接写“解=”、“原式”漏写、中间步骤涉及有理数的运算－计算错误较多、过程书写不规范、如4×写成4、特殊三角函数值记忆不准确，sin45o值错记为、、等。2．解分式方程不会确定最简公分母，或两边同时乘以最简公分母后化简错误，或是将方程的左边进行通分运算，使解题过程不规范；没有检验或把检查作为一种形式，代入最简公分母后不经过计算直接填写不等于0，将无解的方程得解，导致失分。3．求事件的概率题没有过程直接写出结果、或列表画树状图后没有必要的表述直接写出结果导致失分。4．尺规作图题是失分率较高的题目。学生不懂什么是尺规作图，用量角器量角度，用刻度尺量线段，不能正确作图、不会写作法或作法表述不清晰。(三)本题满分7分，平均得分5.76分。本题考查通过扇形统计图获取数据信息，正确理解统计结果,根据数据信息求出相关的统计量、绘制条形统计图，并能用样本估计总体。本题得分率较高。学生答卷存在以下问题：个别统计量概念不清，计算不准确，统计图绘制不规范。失分最多的是将样本容量“200”写成“200人”。(四)本题满分7分,平均得分4.75分。本题考查学生逻辑推理及合情推理能力。设问分两问，第一问需要通过证明三角形全等得出线段相等的结论；第二问在第一问的基础上，增加条件后判断四边形的形状并加以证明。涉及知识点有运用斜边直角边定理判定两直角三角形全等、全等三角形的性质、正方形的判定定理。答卷中反映出以下问题：典型问题有：⑴错把HL写成SSA（没扣分），反映学生思路不是很清晰；在没有给出等腰的条件下，误用三线合一、误用两“底角”相等；⑵不按先判断再证明的顺序回答问题；正方形的判定方法思路混乱，对已知条件所指向的思考方向把握不准确，不会用最直接的方法判断。已知条件给出了三个直角且第一问中已证一组邻边相等，显然运用“有一组邻边相等的矩形是正方形”11 来判断最简捷，但有相当一部分学生绕了很大的弯路或证明平行四边形或证菱形、部分学生仍用正方形最初定义进行判断，没有掌握正方形的判定定理，推理过程不严密等。（五）本题满分8分，平均得分4.27分。本题考查切线的性质、勾股定理、扇形的面积公式以及运用三角函数的定义通过特殊三角函数值求出扇形的圆心角。本题得分率偏低，答题存在的问题如下：1．思路不清，用SSA证明三角形全等；没有说明垂直关系直接运用勾股定理；符号语言表达不清，如辅助线的作法正确表述为“连接OC”，相当一部分学生表述为“作OC⊥AB”，或图中画出辅助线但解题过程中没有表述辅助线的作法。2．切线的性质、等腰三角形三线合一性质等基础知识不会用，扇形的面积公式记忆不准确等。3．结论不写单位等。（六）本题满分10分，平均得分3.18分。本题以贴近生活实际的服装销售问题为素材考查学生建立方程（或方程组）、不等式等数学模型解决实际问题的能力。问题设置分为三个层次,涉及销售打折问题、增涨率问题、建立不等式模型解决获利问题，由于问题是递近式的问题，各问之间有连续性，所以制定评分标准时，考虑到学生只要能正确分析数量关系，列出的方程是正确的，不会因第一问计算的失误影响第二问列方程的得分。阅卷过程中发现解答存在以下问题：1.部分学生对于销售问题不能正确分析进价、售价、利润、折扣之间的数量关系构建数学模型。2.关于增涨率问题，学生列方程情况较好，但解答过程中不能选择恰当的解法（直接开平方法），使解题准确率不高。3.解答过程不注重细节。如设未知数字母多次使用同一个字母、对不符合实际意义的解需要舍去不够重视、题目要求答案取整数部分学生不按要求答题。(七)本题满分13分，平均得分3.39分。本题以平面直角坐标系中两个全等直角三角形为载体，研究图形在平移变换中，特殊位置的点的坐标、二次函数的解析式，动圆与坐标轴的特殊位置关系、以及在整个运动过程中叠合部分面积与运动时间的函数关系。重点考查学生综合运用知识解决问题的能力及学生思维水平。11 题目设问首先是在静止状态、特殊位置求点的坐标及二次函数的解析式，学生可以进门，但求解析式时，学生如果充分感知到整个变化过程中图形为轴对称图形，将解析式设为顶点式，会给解决问题带来很大便捷；第三问涉及图形的运动，学生考虑时需要按照运动时间分类讨论，第一时间段需要学生独立画出图形，第二时间段，需要对整个运动变化过程中的对称关系有充分的理解，不易突破。答题反映出的问题如下：1．第⑴问学生能求出OB的长，但点B的坐标写错，没有考虑到第二象限点的横坐标为负数。2．第⑵问求解析式多设为三点式，导致计算量增大，准确率低。求点P的坐标写出一个答案的较多，反映出学生考虑问题数形结合意识欠缺、考虑问题不全面。3．第⑶问能突破的学生较少。大部分学生因为第一时间段没有给出图形，只求出了第二时间段的函数关系式，说明学生没有分类讨论的思维习惯，缺少自主探索、独立画图解决问题的能力。个别学生求第一时间段重叠部分图形面积时缺乏将不规则图形转化为规则图形的意识。四、答卷中反映出的典型问题1．基础知识掌握不牢固主要表现：⑴概念不清、知识混淆。如因式分解提公因式与配方法提二次项系数混淆、分式方程的解法与分式的加减运算混淆。⑵记忆不准确。如特殊三角函数值错记、扇形面积公式、弧长公式、常用的性质定理、判定定理等记忆不准确。2．学生逻辑推理能力需要加强主要表现：证明过程条理不清、推理过程不严密、不用已知条件直接得结论、罗列无关条件下结论、条件不全下结论、没有推理凭直觉下结论、不能用最简明最直接的方法推导结论、常用的判定定理与性质定理不会用等。3．复习过程中个别知识有疏漏《数学课标》对尺规作图有明确的要求，但从学生答题情况看尺规作图题满分6分，抽样显示平均得分2.34分，得分率仅占39%。阅教教师研讨时一致认为失分较多的原因并非题目难度大，而是复习过程中教师们对这部分知识关注不够，复习疏漏导致失分严重。11 4．审题不清部分学生因审题不清失分。如填空题第5小题，观察规律，根据规律确定的个位数字是多少，有32%的学生没有填出个位数字是8，而是计算出的的最后结果。又如第9题尺规作图明确要求保留作图痕迹并写出作法，有的学生作图痕迹完全正确，但却不写作法；应用题要求结果取整数，部分学生没按要求答题。5．解题不规范，卷面不整洁表现为：⑴解题过程不规范。如：计算题不写解、步骤不全；解分式方程不检验等。⑵作图不规范。如尺规作图题徒手画弧、画线；绘制条形统计图也有徒手作统计图的情况；几何图形中将辅助线画成实线。⑶卷面字迹潦草难以辨认、随意删改、涂抹、不作标识转换答题位置等情况均有。6．分析问题建立数学模型解决问题的能力较差应用题满10分，抽样统计学生平均得分3.18分，从答题情况看相当一部分学生不能合理构建销售问题中的数量关系，从实际问题抽象为数学模型的过程中，表现出分析问题能力欠缺，难以准确找到等量关系，应用意识缺乏，不考虑答案的实际意义。7．学生运用数学思想解决问题的能力欠缺从第七大题学生的答题情况看，大部分生没有分类讨论与数形结合的想法。比如最后一问大部分学生都只求出了给定图形的时间段的函数关系式，而没有给出具体图形的时间段的函数关系式就没求出来，一方面学生不会根据时间段分类讨论，另一方面缺乏准确作出几何图形，将函数关系与图形结合起来的意识。五、教学建议1．认真落实《课程标准》从学生答题失分较多的题目看，教学过程中对近几年没考的知识点关注不够，凭经验进行复习，存在考什么就重点关注什么的教学倾向，考试内容并非一成不变，建议认真研读《课程标准》，把握好课标对知识目标的不同层次要求，具体目标要求是了解、理解、掌握还是灵活运用，要做到心中有数。按不同层次的要求在教学过程中严格落实。2.重视概念教学从答题情况分析看，许多学生失分于基础知识不扎实、概念不清。11 数学概念是数学知识中最基本、最重要的知识，是其他思维形式的基础。只有掌握了概念才能运用概念进行判断、推理和论证。虽然教材中有些概念淡化了，但只是淡化了概念的名词，比如提公因式教材中是结合具体例题明确了提公因式的要求，是再运用中体会概念的本质，教学中必须将概念的本质剖析透彻。重视概念的形成过程，为学生提供实际生活中的现实原型，通过感知实例引导学生真正理解概念的本质，经历抽象概括的过程，用文字语言和符号语言准确表述，几何概念还要结合图形语言理解。并且要通过适当的运用，及时深化对概念的理解。3.加强审题能力的培养学生答题情况反映出由于审题不清导致失分的较多。有对题意理解有误的、有不按题目要求答题的、有答非所问的等等。建议平时教学中有意识地培养学生的审题能力，从点滴入手养成独立审题的良好习惯。4．教学中要关注证明的基本过程和基本方法学生答题中明显反映出推理能力需要加强。建议教学中加强逻辑推理能力的训练，注意纠正条件不全下结论，或罗列无关条件下结论的不良习惯。引导学生清晰地、有条理地表达自己的思考过程，养成良好的说理习惯与书写习惯。做到言之有理，落笔有据。对于推理能力的培养不要局限于“空间与图形”，而是要结合各内容领域不失时机地进行。5.教学中注重培养学生规范书写、规范作图的习惯学生答题及作图的规范性需要加强，有些细节需要教学中加以强调，如辅助线画成实线，因式分解时相同因式不写成幂的形式，这些情况需要在教学中提出规范的要求。另外学生书写不规范与教师教学过程中存在随意性的教学行为有一定的关系，如教学过程中教师徒手画图，图形不够准确的现象很常见；解决问题只分析解题思路或证明思路，具体书写步骤略过的现象也常见，这些都给学生负面的影响。建议教学中加强教师的示范作用，必要的解题步骤、典型的例题解答过程要给出规范的示范。重视学生画图技能的培养，画图要准确、干净、正确反映位置关系，画高质量的几何图形对培养学生的空间观念有着重要的意义。6．教学中要联系实际、突出建立数学模型的思想、加强学法指导分析应用题、正确寻找数量关系是学生解答应用题的一个突出弱点。教学中要注重让学生在实际背景中理解数量关系，增强应用意识，加强解决实际问题能力的训练，加强学法指导，教给学生认真审题和寻找等量关系的方法，11 教给学生辅助分析问题的方法，如线段图、示意图、列表法等，让学生学会画图、列表分析题意找等量关系，直观形象地加深了对数量关系的理解。教学中还要重视解题后的规律总结、方法提炼，培养学生把实际问题数学化的能力。7．重视数学思想方法、关注学生思维的发展“数学是思维的科学”，学生数学思维的发展，不能代替也无法传传递，只有通过自已的思考建立起自己的数学理解能力时，才能真正学好数学。因些在教学过程中要给学生充分的独立考的时间和空间，给学生暴露思维过程的机会。有意识地进行思维训练。很多教师有这样的困惑，学生总是停留在模仿水平上，只要条件稍加变化，就不知所措，学生一直不能形成较强的解决问题的能力。究其原因，说明学生没有掌握解决问题的思想方法。课程标准明确指出：“义务教育阶段要使学生获得进一步发展所必须的基础知识、基本技能、基本思想方法与基本活动经验。”因此，建议教学中将渗透数学思想方法纳入教学目标，不失时机地在概念教学中渗透数学思想，在命题证明中展示数学思想，每一个命题、定理的证明过程都蕴含着一定的思想方法。在解题过程中感悟数学思想，在知识总结中概括数学思想方法。比如函数部分就可以让学和充分感受到数学思想方法的训练与熏陶，通过图象研究性质感悟数形结合思想、通过具体函数性质归纳一般函数性质体会特殊到一般思想、分情况讨论函数性质渗透分类讨论的思想、通过对比不同函数的性质感受类比的数学思想，增强学生对数学思想方法的应用意识，运用基本的数学思想方法有利于数学的理解、记忆、迁移，从而较快地提高学生的学习效率和良好的思维品质。如果将学生的数学素质看作一个坐标系，那么知识技能好比横轴上的内容，而数学思想方法就相当于纵轴上的内容，教师必须从两个维度上把握好数学学科的基构结构，才能从根本上提高学生学习能力和思维品质。2012年8月31日11