阿贝尔分部求和公式的推广及应用.doc 11页

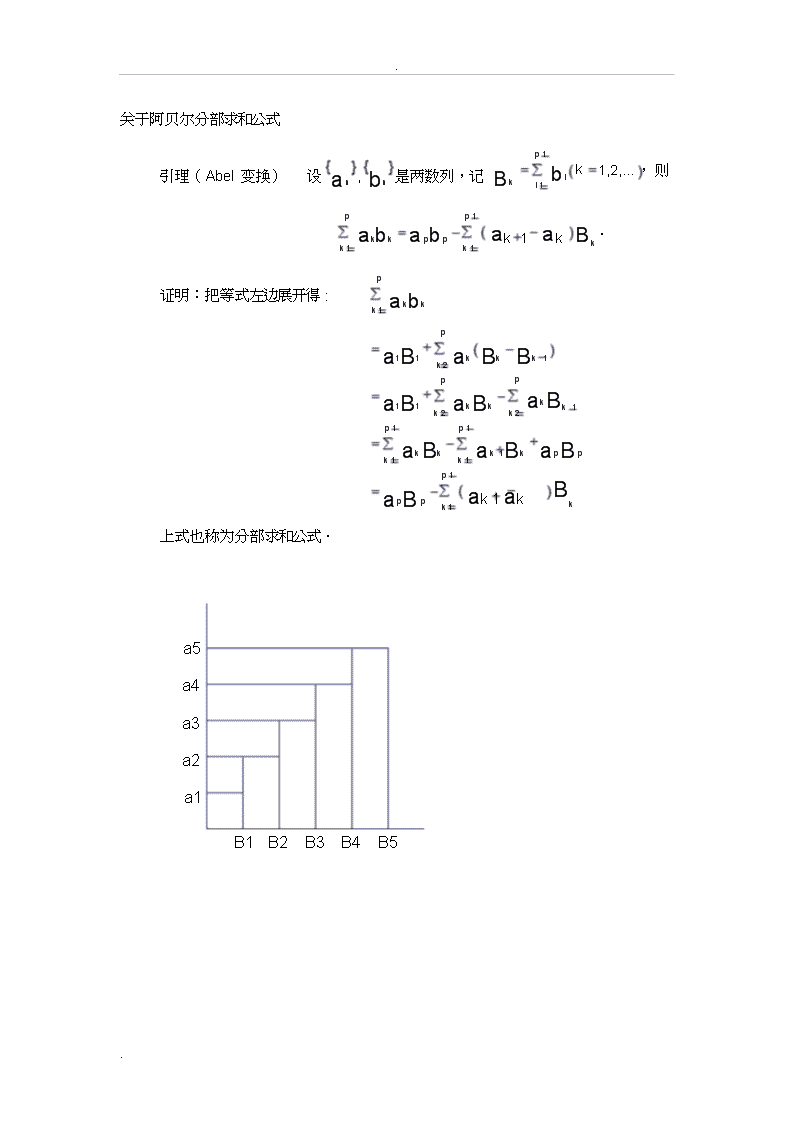
.关于阿贝尔分部求和公式p1引理（Abel变换）设an,bn是两数列，记Bkbik1,2,...，则i1pp1k1akbkapbpB．k1ak1akkp证明：把等式左边展开得:k1akbkpa1B1k2pakBkBk1pa1B1p1k2akBkp1k2akBk1k1akBkk1ak1BkapBpp1apBpk1ak1akBk上式也称为分部求和公式．a5a4a3a2a1B1B2B3B4B5. ...上图是当an0,bn0，且an单调增加时，Abel变换的直观的示意．图....中矩形0,B50,a5被分割成9个小矩形，根据所标出的各个小矩形的面积，..即得到p=5的Abel变换：aak54..abaBkk55k1k1kBk1..x事实上，Abel变换就是离散形式的分部积分公式．记Gxag(t)dt,则分部积分公式可以写成bb..f(xg)ax(dx)f(b)Gb()aGxdf(x)．..将数列的通项类比于函数，求和类比于求积分，求差类比于求微分，..ak1－ak对应于dfx，则两者是一致的．三阿贝耳分部求和公式的推广及应用..（一）关于数论方面的推广和应用定理1设x1，b(n)是一个数论函数，Bxbn．nx..再设ax是区间x1,x2上的连续可微函数，x2>x10.那么有....anbn＝aB＿aB＿x2Bxa"xdx．..x1nx2x2x2x1x1x1....证明：设n1＝x1，n2＝x2．我们有（约定B0＝0）....x1na(n)b(n)=anbnx2x10,对一切k，成..立BkM，则. ...pabkkMk11a2ap．..证明：由Abel变换可得，..由于akpabkkk1单调，所以apBpp1aaBk1kkk1Mapp1aak1kk1....p1ak1k1ak＝apa1．....pabkkMk11a2ap....定理1（级数的Abel判别法）anban单调有界，n收敛，则级数bnn1n1..敛．..证明：设anM，由于n收敛，则对于任意给定的＞0，存在正整bn1..数N，使得对于一切n>N和pN,成立pnbk＜.k1npnba对于kk应用Abel引理，即得k1n..pnbakk＜k1nan12apn3M.....定理2（阿贝耳定理）设an＝s,则limnanx＝s...n0x1n0..证明：容易看出nanx＝f(x)在0n0x1上为一致收敛．事实上，对. ...np任给正数，有N使得当n>N时akkn＜．从而由阿贝耳引理可知同时有....npxxnakk＜，只要0knx1．因此由函数数项级数的连续性定理可得..limf(x)＝f(1)＝s.x1..定理2(级数乘法原理)令cna0bna1bn1...anb0．又设级数....an,bn,cn都收敛．则cabnn．nn0n0n0..证明：因为绝对收敛的级数可以相乘，因此xacxbxnnnnnnn0n0n0..＝s1(x)s2(x)（0x1）..于是由阿贝耳定理便可得到..cnlimncnx＝lims1(x)s2(x)＝lims1(x)lims2(x)..n0x1n0x1x1x1..abss＝1(1)2(1)＝nn．n0n0例题1试证..111121111111111..2(1234...)(1)232142351234n11.....证明：应用阿贝耳关于级数乘法的定理，取an＝bn＝a0=b0=0,则有n（n=1,2,3,⋯）,n..cn＝a1bn1a2bn2．．＋an1b1＝1n，..此处. ...111＝...1(n2)..n1n12n23n3n11....显然有nn=(1+1)+(2+n11n2)+⋯+(1+1)n1....=2(1+1+⋯+12n1)＝2lnn＋2+o(1)(n)..其中为欧拉常数．于是n0．又因为..（n+1）－n＝2..n1nn..n（n－n1）＝n1－［（n+1）n1－nn］=2n1－>0n..故得n0．..从而由莱布尼兹收敛判别法可见级数n＝cn0n2n1n是收敛的，..最后由级数乘法原理可知该命题是成立的．..例题2设0,0,p0．试证二重级数comsnp..m,nmn为收敛的．分析：不难看出mn11..sm,nk1j1coskj4cos2cos2..以及m1bm,n－bm1,n＝mpdxxnp10，..bm,n－－bm,n1＋bm1,n1. ...m1n1mn=dxp(p1)dy0，..p2xy..其中bm,n＝pmn0（当m+n时）．..2．关于级数求和问题..例题11...=ln2.111234n11n..证明:当0xn111时，可得1n11nnx＝ln(1+x)..故得＝limnxlimln(1+x)＝ln2...1x11nx1..例题2设a1,b1,ab.求证....1＝1ab1xxdx..n1nanbba01x证明：显然左端的级数是收敛的，把它写成1＝1.11，n1nanbban1nanb而作函数..f(x)＝1ba1nanbxx（x1）nanb..从而..1f"x(＝)na1xnb11x＝ab（xx）．..ba1ba1x1x由于f(0)＝0,故. ...xf(x)＝ab1(tt)dt（0x1）..0ba1t因此，应用定理便可得到要证明的等式．（三）关于连续变量的阿贝耳分部求和公式及其应用当下标n变成连续变量时，与和差变换相应的是分部积分公式，与阿贝耳引理相应的是鲍纳的积分中值定理．我们已经熟悉掌握了黎曼积分的初步知识，所以这里可以把一些命题变成较一般的形式．..ba定理1（分部积分法）设黎曼积分(x)df(x)存在，则bf(x)da(x)也存在，..并且有分部积分公式..bf(x)da(＝xbbf(x)(x)a－a(x)df(x)．..证明：以表示［a,b］的任意划分：..：a=x0x1...=b,..x2xn并记＝max(xvxv1)（1vn）.应用和差变换于积分和..n,fkxkk1xk1，....其中计值点组,,...12n适合xk1kxk（k=1,2,⋯,n）,我们..得到..n1xk,()[f()k1k1f()](xkn)f(n)(x0)f()1....1＝(a)[f()f(a)]n1xk()[f()k1k1f()]k....(b)[f(b)f()](b)f(b)(a)f(a)n. .＝,(b)f(b)(a)f(a)，..其中为划分a012...b，nn1..而计值点组＝(a,x1,x2...,xn1,b)，..ba1于是,为积分(x)df(x)的积分和，并且＝....max()2(vv1vn1)..所以令0时，便得..bf(x)da(x)＝lim,lim,(b)f(b)(a)f(a)00..ba＝－(x)df(x)＋(b)f(b)(a)f(a)..注意：若f(x)连续而(x)为有界变差的函数，则积分bf(x)da(x)存在．..而由本命题可知，当(x)为连续而f(x)为有界变差时，积分bf(x)da(x)也存在．..定理2（第一中值定理）设(x)为一单调函数而f(x)为实值连续函数，则有中值公式..bf(x)da(x)＝f()(b)(a)（ab）．..提示：此命题的证法与通常黎曼积分的中值公式证法相似．定理3（第二中值定理）设在［a,b］上(x)为一实值连续函数而f(x)为一单调函数．则必有,ab，使得..bf(x)da(＝xf(a)＋d(x)f(b)abd(x)．..提示：应用分部积分公式后再应用第一中值定理即得．12例题1设g(x)和g(x)满足..xxa1ag(t)dtg2(t)dt(axb)..bb1aag(t)dtg2(t)dt．..又设f(x)为非增函数，则. .bb..af(x)g1(x)dxaf(x)g(x)dx2..证明：令G(t)=xag2(t)g1(t)dt,则G(x)0(axb)...G(a)=G(b)=0,所以有..bbaf(t)g2(t)dt－a1bbf(t)g(t)dt＝bf(t)dG(t)a..＝f(t)G(t)a－G(t)df(t)a..b＝－G(t)df(t)0．abbab..b例题2不等式f(t)dtf(t)g(t)dtaaf(t)dt（1）（式中g(t)dt）a....对每一个不增的函数f(t)都成立的充分必要条件是函数g(t)对所有..x[a,b]满足..b且0g(t)dtbx0xxag(t)dtxa(2)成立．....证明：必要性：设f(t)1(tx)，则不等式(1)给出xag(t)dtxa（axa），（3）..0(tx)bg(t)dt0(axb),x(4)设axb，则有(4)得..(xa)x=g(t)dt(xaab+)g(t)dt0.x..设axa，则有（3）得..bxg(t)dt＝－xag(t)dt－（xa）＝a＋－x0..所以（3）和(4)对所有的x[a,b]都成立．同样可证..x，g(t)dt0abg(t)dtbxx..对于所有的x[a,b]成立．所以当不等式（1）对所有的不增的f(t)成立时不等式(2)成立．. .充分性：由已知可得aaf(t)dt－bf(t)g(t)dt＝aaaf(t)f(a)1g(t)dtb＋af(a)f(t)g(t)dtI1I2利用分部积分公式bbbxa(x)f(x)dx(fa)b(t)dt(aa(tdtdfx容易看出当（2）式成立时aI1＝I2＝ax1g(t)dtdf(x)abaaxaxg(t)dtdaf(t)0bag(t)dtdf(x)0x所以（1）右边的不等式成立．同样的道理可以证明左边的不等式也成立．.