达朗贝尔公式课件.ppt 16页

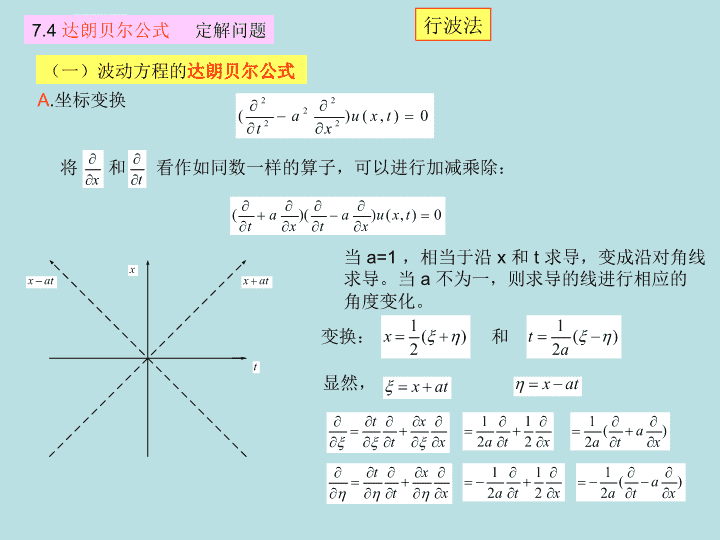
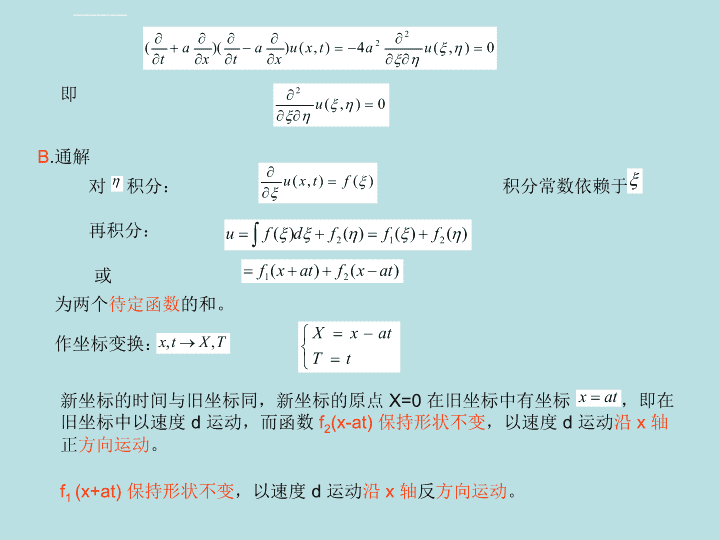
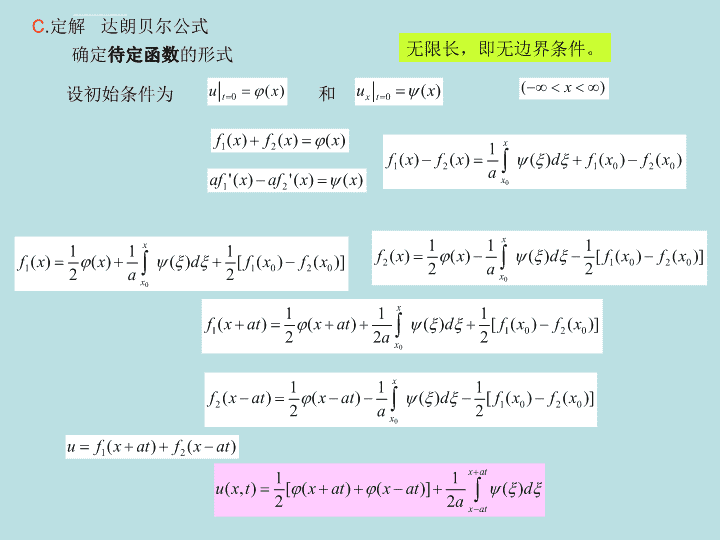
7.4达朗贝尔公式定解问题（一）波动方程的达朗贝尔公式将和看作如同数一样的算子，可以进行加减乘除：当a=1，相当于沿x和t求导，变成沿对角线求导。当a不为一，则求导的线进行相应的角度变化。变换：和显然，A.坐标变换行波法 即B.通解对积分：积分常数依赖于再积分：或为两个待定函数的和。作坐标变换：新坐标的时间与旧坐标同，新坐标的原点X=0在旧坐标中有坐标，即在旧坐标中以速度d运动，而函数f2(x-at)保持形状不变，以速度d运动沿x轴正方向运动。f1(x+at)保持形状不变，以速度d运动沿x轴反方向运动。 C.定解达朗贝尔公式确定待定函数的形式无限长，即无边界条件。设初始条件为和 例 例解： （二）端点的反射一个端点固定设初始条件为和边界条件达朗贝尔公式是无限长弦的公式。自变量限制为。时，上式中后两项无意义。必须将u(x,t)延拓到这个范围。，作奇延拓： 半波损失 一个端点自由设初始条件为和边界条件应该是偶延拓 无半波损失 （三）跃变点的反射无限长杆，x<0，x>0两部分的杨氏模量和密度分别为。x=0是跃变点。设有行波从区域I向x=0点运动。到x=0产生反射和透射。取此波在t=0时刻抵达x=0.衔接条件区域I中的行波： 区域II中，只有透射波衔接条件 又反射系数透射系数 从达朗贝尔公式可以看出，波动方程度解，是初始条件的演化。方程本身并不可能产生出超出初始条件的，额外的形式来。而这种演化又受到边界条件的限制。这就说明了初始条件和边界条件在确定波动方程度解时的重要性。 习题7.4.1解：习题7.4.6设初始条件为和边界条件