达朗贝尔原理(动静法)课件.ppt 58页

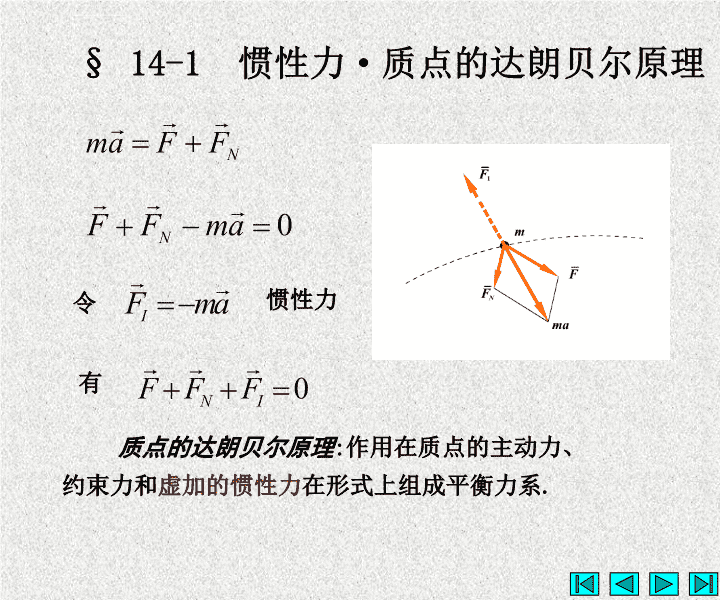
第十四章达朗贝尔原理(动静法)惯性力达朗贝尔原理刚体惯性力系的简化绕定轴转动刚体的轴承动约束力 前面介绍的动力学普遍定理,为解决质点系动力学问题提供了一种普遍的方法。达朗贝尔原理为解决非自由质点系动力学问题提供了另一种普遍的方法。这种方法的特点是：用静力学研究平衡问题的方法来研究动力学的不平衡问题,因此这种方法又叫动静法。由于静力学研究平衡问题的方法比较简单,也容易掌握,因此动静法在工程中被广泛使用。 §14-1惯性力·质点的达朗贝尔原理令惯性力有质点的达朗贝尔原理:作用在质点的主动力、约束力和虚加的惯性力在形式上组成平衡力系. 例14-1已知:求:用达朗贝尔原理求解 解:解得 例14-2球磨机的滚筒以匀角速度w绕水平轴O转动,内装钢球和需要粉碎的物料,钢球被筒壁带到一定高度脱离筒壁,然后沿抛物线轨迹自由落下,从而击碎物料,如图。设滚筒内壁半径为r,试求钢球的脱离角a。解：以某一尚未脱离筒壁的钢球为研究对象,受力如图。钢球未脱离筒壁前,作圆周运动,其加速度为惯性力FI的大小为假想地加上惯性力,由达朗贝尔原理OMrwaqFFNmgFI这就是钢球在任一位置q时所受的法向反力,显然当钢球脱离筒壁时,FN＝0,由此可求出其脱离角a为 §14-2质点系的达朗贝尔原理记为作用于第i个质点上外力的合力.为作用于第i个质点上内力的合力.则有质点系的达朗贝尔原理:质点系中每个质点上作用的主动力,约束力和它的惯性力在形式上组成平衡力系. 因有也称为质点系的达朗贝尔原理:作用在质点系上的外力与虚加在每个质点上的惯性力在形式上组成平衡力系. 已知：如图所示,定滑轮的半径为r,质量为m均匀分布在轮缘上,绕水平轴Ｏ转动.垮过滑轮的无重绳的两端挂有质量为m1和m2的重物(m１>m2),绳与轮间不打滑,轴承摩擦忽略不计。求：重物的加速度.例14-3 解:由解得 已知：飞轮质量为m,半径为Ｒ,以匀角速度　定轴转动，设轮辐质量不计,质量均布在较薄的轮缘上,不考虑重力的影响.求:轮缘横截面的张力.例14-4 解:令 例14-5重P长l的等截面均质细杆AB,其A端铰接于铅直轴AC上,并以匀角速度w绕该轴转动,如图。求角速度w与角q的关系。解：以杆AB为研究对象,受力如图。杆AB匀速转动,杆上距A点x的微元段dx的加速度的大小为微元段的质量dm＝Pdx/gl。在该微元段虚加惯性力dFI,它的大小为xdxdFIanqwBACyxqBAxdPFAxFAyFI于是整个杆的惯性力的合力的大小为 设力FI的作用点到点A的距离为d,由合力矩定理,有即假想地加上惯性力,由质点系的达朗贝尔原理qBAxdPFAxFAyFI代入FI的数值,有故有q＝0或 用质点系的达朗贝尔原理求解质点系的动力学问题，需要对质点内每个质点加上各自的惯性力，这些惯性力也形成一个力系，称为惯性力系。下面用静力学力系简化理论，求出惯性力系的主矢和主矩。以FIR表示惯性力系的主矢。由质心运动定理及质点系的达朗贝尔原理得此式表明：无论刚体作什么运动,惯性力系的主矢都等于刚体的质量与其质心加速度的乘积,方向与质心加速度的方向相反。§14-3　刚体惯性力系的简化 由静力学中任意力系简化理论知，主矢的大小和方向与简化中心的位置无关，主矩一般与简化中心的位置有关。下面就刚体平移、定轴转动和平面运动讨论惯性力系的简化结果。又因为所以有即无论刚做什么运动，惯性力主矩主矢可由下式计算： １刚体平移惯性力系向质心简化.只简化为一个力惯性力系向点O简化.平移刚体的惯性力系可以简化为通过质心的合力，其大小等于刚体的质量与加速度的乘积，合力的方向与加速度方向反向。 2刚体定轴转动 由有记为对于z轴的惯性积.同理 如果刚体有质量对称面且该面与转动轴垂直,简化中心取此平面与转轴的交点,则综上可得结论：定轴转动刚体的惯性力系,可以简化为通过转轴O的一个惯性力FIR和一个惯性力偶MIO。力FIR的大小等于刚体的质量与其质心加速度大小的乘积,方向与质心加速度的方向相反，作用线通过转轴；力偶MIO的矩等于刚体对转轴的转动惯量与其角加速度大小的乘积,转向与角加速度的转向相反。 现在讨论以下三种特殊情况：2.当刚体作匀速转动时,a＝0,若转轴不过质心,惯性力系简化为一惯性力FI,且FI＝－maC,同时力的作用线通过转轴O。1.当转轴通过质心C时,aC＝0,FI＝0,MIC＝－JCa。此时惯性力系简化为一惯性力偶。3.当刚体作匀速转动且转轴通过质心C时,FI＝0,MIC＝0,惯性力系自成平衡力系。 ３　刚体作平面运动（平行于质量对称面）向质心简化结论：有质量对称平面的刚体，平行于此平面运动时，刚体的惯性力系简化为在此平面内的一个力和一个力偶。这个力通过质心，其大小等于刚体的质量与质心加速度的乘积,其方向与质心加速度的方向相反；这个力偶的矩等于刚体对过质心且垂直于质量对称面的轴的转动惯量与角加速度的乘积,转向与角加速度相反。 已知：如图所示均质杆的质量为m,长为l,绕定轴O转动的角速度为,角加速度为.求：惯性力系向点Ｏ简化的结果(方向在图上画出).例14-6 解: 已知：如图所示,电动机定子及其外壳总质量为m1,质心位于O处.转子的质量为m2,质心位于Ｃ处,偏心矩ＯＣ＝e,图示平面为转子的质量对称面.电动机用地角螺钉固定于水平基础上,轴O与水平基础间的距离为h.运动开始时,转子质心Ｃ位于最低位置,转子以匀角速度　转动.求：基础与地角螺钉给电动机总的约束力.例14-7 解:因 已知：如图所示,电动绞车安装在梁上,梁的两端搁在支座上,绞车与梁共重为P.绞盘半径为R,与电机转子固结在一起,转动惯量为J,质心位于O处.绞车以加速度a提升质量为m的重物,其它尺寸如图.求：支座A，B受到的附加约束力.例14-8 解:解得: 上式中前两项为静约束力,附加约束力为 已知：均质圆盘均质杆纯滚动.求：F多大,能使杆B端刚好离开地面?纯滚动的条件?例14-9 解:刚好离开地面时,地面约束力为零.研究AB杆 解得研究整体得解得 DBA例14-10如图所示,均质杆AB的质量m＝40kg,长l＝4m,A点以铰链连接于小车上。不计摩擦,当小车以加速度a＝15m/s2向左运动时,求D处和铰A处的约束反力。解：以杆为研究对象,受力如图,建立如图坐标。杆作平动,惯性力的大小为FI＝ma。假想地加上惯性力,则由质点系的达朗贝尔原理于是得FIlA30°DBh＝1maaFDmgFAxFAyxy 代入数据,解之得：DBAFIaFDmgFAxFAyxy BC例14-11均质杆AB长l,重W,B端与重G、半径为r的均质圆轮铰接。在圆轮上作用一矩为M的力偶,借助于细绳提升重为P的重物C。试求固定端A的约束反力。解：先以轮和重物为研究对象,受力如图。假想地加上惯性力由质点系的达朗贝尔原理aMGFBxFByMIBaPFIC代入MIB和FIC得 再以整体为研究对象,受力如图,假想地加上惯性力BCAaMGFAxFAyMIBPFICaWmA代入MIB和FIC解得由质点系的达朗贝尔原理 jOxyCBA质量为m,长为l的均质直杆AB的一端A焊接于半径为r的圆盘边缘上,如图。今圆盘以角加速度a绕其中心O转动。求圆盘开始转动时,AB杆上焊接点A处的约束反力。解：以杆为研究对象,受力如图,建立如图坐标。将惯性力系向转轴简化,惯性力的大小为aOrABlamgaCFIMIOFAxFAymA 由质点系的达朗贝尔原理CBAamgaCFIMIOFAxFAymAjOxy将已知数值代入以上三式,解之得 qrC例14-12重P、半径为r的均质圆轮沿倾角为q的斜面向下滚动。求轮心C的加速度,并求圆轮不滑动的最小摩擦系数。解：以圆轮为研究对象,受力如图,建立如图坐标。圆轮作平面运动,轮心作直线运动,则将惯性力系向质心简化,惯性力和惯性力偶矩的大小为qCrFSFIMIFNPaxyaC则由质点系的达朗贝尔原理 解之得由于圆轮没有滑动,则F≤fN,即由此得所以,圆轮不滑动时,最小摩擦系数qrCFSFIMIFNPaxyaC 例题14-13已知两均质直杆自水平位置无初速地释放。求两杆的角加速度和O、A处的约束反力。解:(1)取系统为研究对象ABOMI1MI2mgmgFI2FI1FOyFOxBAO12 (2)取AB杆为研究对象MI2mgFI2FAyFAxBA2 (3)取AB杆为研究对象MI2mgFI2FAyFAxBA2 (4)取系统为研究对象MI1MI2mgmgFI2FI1FOyFOxBAO12 例14-14均质杆的质量为m,长为2l,一端放在光滑地面上,并用两软绳支持,如图所示。求当BD绳切断的瞬时,B点的加速度AE绳的拉力及地面的反力。解：以AB杆为研究对象,杆AB作平面运动,如图,以B点为基点,则C点的加速度为其中将惯性力系向质心C简化,得惯性力FI＝FIe＋FIr,其中FIe＝maB,FIr＝matCB＝mla和惯性力偶,其力偶的矩为AECBxy30oBCAED30oFTFNmgFIeFIrMIaBaBatCBa在BD绳切断的瞬时,受力如图,建立如图坐标。 由质点系的达朗贝尔原理AECBxy30oFTFNmgFIeFIrMI BA30ox以B为基点,则A点的加速度为其中将上式投影到x轴上得联立求解（1）~（4）式,得aBaBatABaatA 例14-15如图所示,均质杆AB长为l,重为Q,上端B靠在半径为R的光滑圆弧上（R=l）,下端A以铰链和均质圆轮中心A相连,圆轮重P,半径为r,放在粗糙的地面上,由静止开始滚动而不滑动。若运动开始瞬时杆与水平线所成夹角,求此瞬时A点的加速度。轮和杆均作平面运动,将惯性力系分别向质心简化,则惯性力和惯性力偶的矩的大小分别为解：设系统运动的初瞬时,圆轮中心的加速度为,角加速度为；AB杆的角加速度为,质心C的加速度为、。如图。 先以整体为研究对象,受力如图。假想地加上惯性力和惯性力偶,则由质点系的达朗贝尔原理(1) 再以AB为研究对象,受力如图。假想地加上惯性力和惯性力偶,则由质点系的达朗贝尔原理（2）AB杆作平面运动,先以B点为基点,则A点的加速度为其中其加速度合成矢量图如图所示。将其投影于轴,得（3） 再以A为基点,则C点的加速度为其中,加速度合成矢量图如图。将其投影于、轴,得（4）（5）由式（3）、（4）、（5）可将、、都化为的函数,即 将其代入式（1）、（2）,并取,联立该两方程可解得 §14-4绕定轴转动刚体的轴承动约束力 解得 即:必有通过质心的惯性主轴称为中心惯性主轴引起的轴承约束力称动约束力,由称满足的轴z为惯性主轴动约束力为零的条件为: 静平衡：刚体的转轴通过质心，刚体除重力外，没有受到其他主动力作用，则刚体在任意位置可以静止不动。动平衡：当刚体的转轴通过质心且为惯性主轴时，刚体转动不出现动约束力。因此,避免出现轴承动约束力的条件是:刚体的转轴应是刚体的中心惯性主轴. 转轴AB与轮盘的质量对称面垂直,但轮盘的质心C不在转轴上,偏心距　　　　　当轮盘以均转速转动.已知：如图所示,轮盘(连同轴)的质量求：轴承A,B的约束力例14-16 解: