一维波动方程的达郎贝尔公式 6页

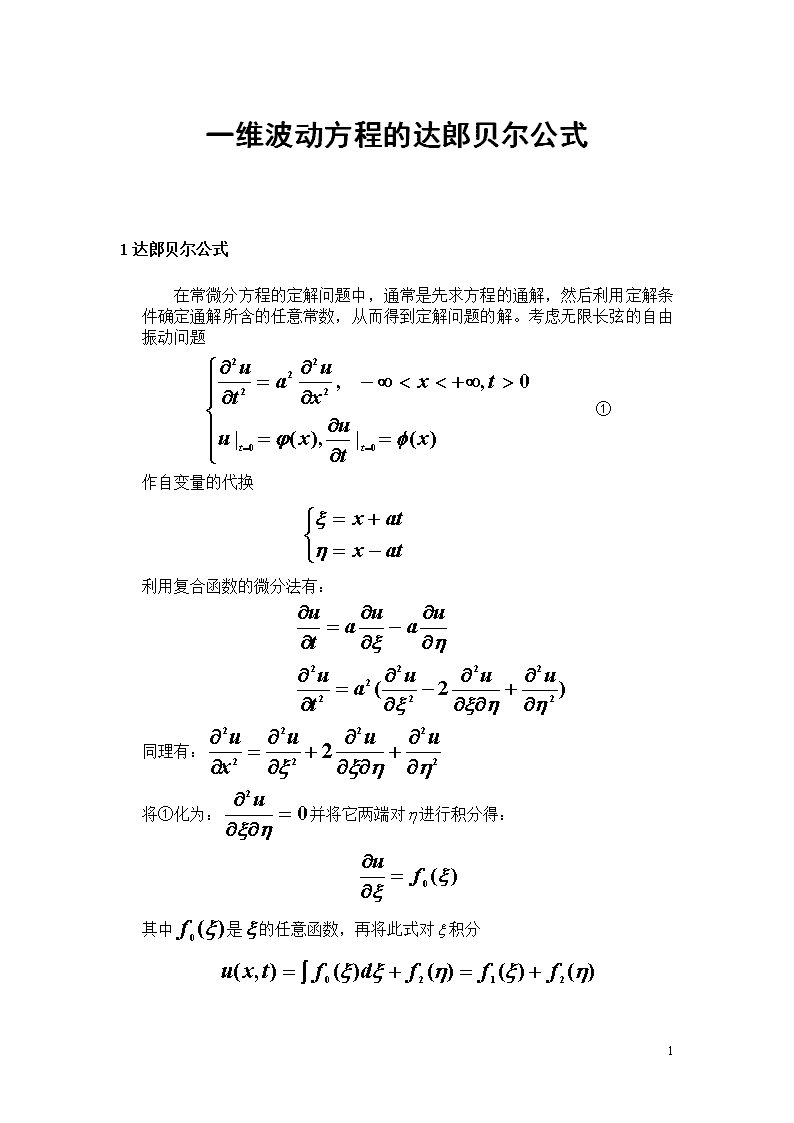
一维波动方程的达郎贝尔公式1达郎贝尔公式在常微分方程的定解问题中，通常是先求方程的通解，然后利用定解条件确定通解所含的任意常数，从而得到定解问题的解。考虑无限长弦的自由振动问题①作自变量的代换利用复合函数的微分法有：同理有：将①化为：并将它两端对进行积分得：其中是的任意函数，再将此式对积分6 ②其中是任意两次连线可微函数，式②即为方程①的含有两个任意函数的通解。由初始条件可得：通过积分可得：称此式为一维波动方程的达郎贝尔公式。2解的物理意义由于波动方程的通解是两部分与。表示了以速度向轴正方向传播的行波，称为右行波。同理，表示了以速度向轴负方向传播的行波，称为左行波。由达郎贝尔公式，解在点的值由初始条件在区间内的值决定，称区间为点的依赖区域，在平面上，它可看作是过点，斜率分别为的两条直线在轴上截得的区间。这里要掌握半无限长弦的自由振动问题和一维非齐次波动方程的柯西问题的解。3半限长弦的自由振动问题定解问题6 用延拓法求解，注意边界条件（4.9），采用奇延拓。令考虑定解问题它的解可由达郎贝尔公式得：。4一维非齐次波动方程的柯西问题　定解问题令，可将此定解分解成下面两个定解问题：6 (I)(II)其中问题(I)的解可由达朗贝尔公式给出：。对于问题(II)，有下面重要的定理。定理（齐次化原理）设是柯西问题的解，则是问题(II)的解。二三维波动方程的柯西问题1三维波动方程的泊松公式考虑三维波动方程的柯西问题(1)三维波动方程的球对称解如果将三维波动方程的空间坐标用球坐标表示，则波动方程化为：6 =如果波函数与，变量无关，而只与变量有关，即是所谓球对称的，这时式可简化为：=即有：。这是关于的一维波动方程，其通解为：从而即得到三维波动方程关于原点为球对称的解。(2)三维波动方程的泊松公式的解为：＋，称它为三维波动方程柯西问题的泊松公式。　这里要求掌握三维波动方程柯西问题的泊松公式的推导过程。6 2降维法利用三维波动方程柯西问题的泊松公式来导出二维波动方程柯西问题的解。这种利用高维问题的解推导低维问题的方法称之为降维法。二维波动方程的柯西的问题：令，将上式的解视为特殊的三维问题，最后得到问题的解为：++称此式为二维波动方程柯西问题的泊松公式。随了掌握这个公式，还要掌握这个公式的物理意义。6