达朗贝尔原理理论力学 74页

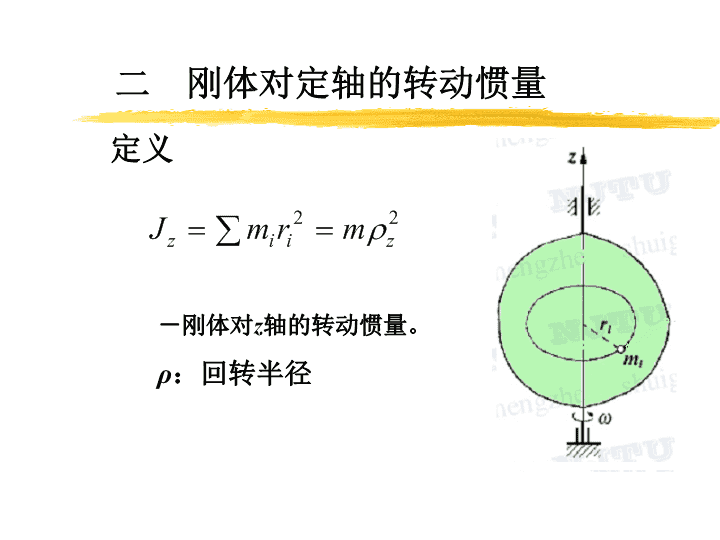
达朗伯原理质点的达朗伯原理质点系的达朗伯原理刚体惯性力系的简化绕定轴转动刚体的轴承动反力 1.预备知识一刚体质心的定义质量均匀分布的规则刚体：质心就是几何中心 定义－刚体对z轴的转动惯量。ρ：回转半径二刚体对定轴的转动惯量 例1求简单物体的转动惯量。(平行移轴）解：由转动惯量的定义：－平行移轴公式 求均质圆盘的J0、Jx、JyP173均质物体的转动惯量 2.质点的达朗伯原理－惯性力2.1原理的描述如果在质点上除作用有主动力及约束力外，再假想地加上惯性力，则这些力构成平衡力系。－质点的达朗伯原理令 质点的达朗伯原理表明，如果在运动着的质点上加上假想的惯性力，则质点处于平衡，因而可将动力学问题在形式上化成静力学问题－动静法。2.2动静法求解惯性力就是求解运动；求解FN就是求解未知的约束力（包括动反力）在已知运动求约束力的问题中，动静法往往十分方便 3.质点系的达朗伯原理一原理描述质点i:质点系的主动力系，约束力系和惯性力系组成平衡力系： 各质点间内力成对出现：作用于质点系上的主动力系，约束力系和惯性力系在形式上组成平衡力系。－质点系的达朗伯原理。六个平衡方程Fx=0Fy=0Fz=0Mx=0My=0Mz=0 所有惯性力组成的力系，称为惯性力系。所有惯性力的矢量和称为惯性力系的主矢：所有力向同一点简化，所得力矩矢量和，称为惯性力系的主矩： 一、刚体平动向质心简化：4.刚体惯性力系的简化ri 二、平面刚体做定轴转动取转轴上任意一点O为简化中心主矢主矩 平面刚体做定轴转动刚体对z轴的惯性积?如果刚体有质量对称面且该面与转轴z垂直；向质量对称面进行简化，取转轴与该面交点为简化中心 平面刚体做定轴转动如果刚体有质量对称面且该面与转轴z垂直；向质量对称面进行简化，取转轴与该面交点为简化中心 如果刚体有质量对称面且该面与转轴z垂直；向质量对称面进行简化，取转轴与该面交点为简化中心平面刚体做定轴转动结论 三、刚体做平面运动（设运动平行于质量对称面）向质量对称面进行简化一般取质心C为简化中心平面运动可以分解为平动＋定轴转动合力偶矩：平动部分为零合力： 例1：anHCaCaCaHyaAaHCεHC 例2： 刚体作平动时（向质心简化）刚体作定轴转动时（转轴与质量对称面垂直，向质量对称面与转轴交点简化）简化结果：刚体作平面运动时（设运动平行于质量对称面、向质心C简化) 解：（1）分析OA、AB杆的运动：例3长均为l，质量均为m的均质杆OA、AB铰接于O，在图示水平位置由静止释放，求初始瞬时OA、AB的角加速度。（2）将OA杆的惯性力向O点简化，AB杆的惯性力向其质心C2简化，做整个系统的受力图：？确定惯性力大小OA作定轴转动，AB作平面运动。设初始瞬时两杆的角加速度分别为1及2。质心加速度分别为ac1及ac2.OABC1C2mgmgFgOFOYFOXMgOFgC2MgC2 （3）考虑系统平衡？列什么方程OABC1C2mgmgFgOFOYFOXMgOFgC2MgC2例3长均为l，质量均为m的均质杆OA、AB铰接于O，在图示水平位置由静止释放，求初始瞬时OA、AB的角加速度。 (4)考虑AB杆平衡:联立(1),(2)求解:OABC1C2mgmgFgOFOYFOXMgOFgC2MgC2ABC2mgFAYFAXFgC2MgC2 例题4均质圆柱体重为W，半径为R，沿倾斜平板从静止状态开始，自固定端O处向下作纯滚动。平板相对水平线的倾角为，忽略板的重量。试求：固定端O处的约束力。解题分析以整体为研究对象，画受力图。？确定惯性力大小 解：1.首先确定圆柱体的质心加速度和角加速度以圆柱体为研究对象，画出包括真实力和惯性力系的受力图。对A点取矩：例题4均质圆柱体重为W，半径为R，沿倾斜平板从静止状态开始，自固定O处向下作纯滚动。平板相对水平线的倾角为，忽略板的重量。试求：固定端O处的约束力。A 2.确定固定端的约束力以整体为研究对象：平衡方程：例题4均质圆柱体重为W，半径为R，沿倾斜平板从静止状态开始，自固定O处向下作纯滚动。平板相对水平线的倾角为，忽略板的重量。试求：固定端O处的约束力。 要点与讨论：在用动静法解题时，应充分运用静力学的解题技巧:让某些未知力通过某个矩心;某些未知力垂直某个投影轴;避免某些未知量在平衡方程中出现，争取一个方程求解一个未知数等。 例5均质直角构件ABC，AB、BC的质量各为3.0kg，l=1.0m。假若突然剪断绳子AE，求此瞬时连杆AD、BE所受的力。连杆AD、BE质量忽略不计。解：研究ABC杆，作受力图：解得由达朗贝尔原理ABC作平移运动初瞬时连杆AD、BE：＝0 例6在图示机构中，沿斜面向上作纯滚动的圆柱体和鼓轮O均为均质物体，各重为P和Q，半径均为R，绳子不可伸长，其质量不计，斜面倾角，如在鼓轮上作用一常力偶矩M，试求：圆柱体A的角加速度。列出平衡方程：取轮A为研究对象，惯性力FIA和惯性力偶MIA解：取轮O为研究对象，惯性力偶矩列出动静方程运动学关系轮A受力图？ 例6在图示机构中，沿斜面向上作纯滚动的圆柱体和鼓轮O均为均质物体，各重为P和Q，半径均为R，绳子不可伸长，其质量不计，斜面倾角，如在鼓轮上作用一常力偶矩M，试求：圆柱体A的角加速度。拓展： 已知：均质圆盘纯滚动.均质杆求：F多大,能使杆B端刚好离开地面?纯滚动的条件?FA加惯性力画受力图a 刚好离开地面时,地面约束力为零.研究AB杆解:研究整体 例题7长为l、重为W的均质杆AB，其A端铰接在铅垂轴z上，并以匀角速绕此轴转动。求:当杆AB与轴间的夹角＝60时，的数值及铰链A处的约束力。?刚体作定轴转动时（转轴与质量对称面垂直，向质量对称面与转轴交点简化） 惯性力合力的大小惯性力合力作用线通过三角形的形心应用动静法，列平衡方程画AB受力图例题7长为l、重为W的均质杆AB，其A端铰接在铅垂轴z上，并以匀角速绕此轴转动。求:当杆AB与轴间的夹角＝60时，的数值及铰链A处的约束力。 5.绕定轴转动刚体的轴承动反力mmABABmmFIFI1FI＝FIFI1>FI2－FIFRAFRB理想状态偏心状态FI2 刚体绕定轴转动时，轴承处除有由主动力引起的约束反力外，由于刚体质量分布不均衡，还可因转动引起附加约束反力，此附加部分称为轴承附加动反力。ABmmABFRBFRAFRAFRB偏角状态既偏心又偏角状态FI－FIFI1FI2mm 例8匀速转动的传动轴上安装有两个齿轮，质量分别为m1、m2，偏心距分别为e1和e2。在图示瞬时，C1D1平行于z轴，该轴的转速是n。求此时轴承A、B的附加动约束力。解：研究AB轴，受力图?根据达朗贝尔原理附加动约束力？ 例9匀速转动的传动轴上安装有两个齿轮，质量分别为m1、m2，偏心距分别为e1和e2。在图示瞬时，C1D1平行于z轴，该轴的转速是n。求此时轴承A、B的附加动约束力。附加动约束力附加动约束力如何消除？惯性力自身成为平衡力系 例10图示装有圆盘的轴可绕水平轴转动。已知：两个质点的质量分别为m1＝0.5kg、m2＝1kg。圆盘的厚度为2cm。密度为7.8×103kg/m3，c＝e＝9cm，b＝18cm。为了动平衡，在盘上离轴d＝8cm处各钻一孔。求孔的直径d1、d2和方位角1、2。解：研究圆盘与轴，其惯性力分别为其中1＝-18.42＝-71.6 将惯性力系向点A简化 —刚体对z轴的惯性积xc，yc为质心在所选坐标系中的坐标应用达朗伯原理列写平衡方程。设刚体上作用有若干主动力Fi 若附加动反力为零转轴必须通过转动刚体的质心，且刚体对该轴的惯性积为零时刚体（转子）是平衡的。物理意义?惯性力自身成为平衡力系 若附加动反力为零转轴必须通过转动刚体的质心，且刚体对该轴的惯性积为零时刚体（转子）是平衡的。刚体的中心惯性主轴：通过转动刚体质心，且为刚体主轴的转轴。刚体的惯性主轴：惯性积为零的转轴。 转轴为刚体的中心惯性主轴（转轴通过转动刚体的质心，且为刚体的一根主轴）时刚体（转子）是平衡的（图（a））。当转轴不通过质心时（图（b）），产生轴承动反力，转子不平衡；由于这种不平衡可以用静力学的方法发现,故称静不平衡。当转轴不是主轴时（图（c）），转子是动不平衡的，因为这种不平衡必须通过转动发现。借助动平衡机，用在转子上钻孔的方法改变刚体质量的分布，可以使转子成为动平衡的（图（d）、（e））。 习题6-1~6习题要求1）基本公式要列明；2）分别画出运动状态参量图和受力图； 1.刚体作平动时（向质心简化）2.刚体作定轴转动时转轴与质量对称面垂直，向质量对称面与转轴交点简化写出刚体做以下运动时，各惯性力系的简化结果：3.刚体作平面运动时设运动平行于质量对称面、向质心C简化 质点系的达朗伯原理作用于质点系上的主动力系，约束力系和惯性力系在形式上组成平衡力系。－质点系的达朗伯原理复习总结平衡方程Fx=0Fy=0Fz=0Mx=0My=0Mz=0 根据质点系的达朗伯原理，可将动力学问题在形式上化成静力学问题，用静力学的方法求解动力学问题－动静法。求解惯性力就是求解运动；求解FN就是求解未知的约束力（包括动反力）。动静法 在用动静法解题时，应充分运用静力学的解题技巧:让某些未知力通过某个矩心;某些未知力垂直某个投影轴;避免某些未知量在平衡方程中出现，争取一个方程求解一个未知数等。 刚体作平动时（向质心简化）刚体作定轴转动时（转轴与质量对称面垂直，向质量对称面与转轴交点简化）常见运动惯性力的简化结果：刚体作平面运动时（设运动平行于质量对称面、向质心C简化) 简单物体的转动惯量－平行移轴公式 均质圆盘P173均质物体的转动惯量 例11已知：均质杆AB的质量为m，球铰链A和绳子BC与铅垂轴OD相连，绳子的重量略去不计，小环可沿轴滑动，如图示。设AC＝BC＝l，CD＝OA＝l/2，匀角速度为，求绳子的张力、铰链A的约束力及轴承O、D的附加动约束力。解：研究AB杆，画受力图作用点在距A点(2/3)处以整体为研究对象,作受力图求惯性力由达朗贝尔原理 例11已知：均质杆AB的质量为m，球铰链A和绳子BC与铅垂轴OD相连，绳子的重量略去不计，小环可沿轴滑动，如图示。设AC＝BC＝l，CD＝OA＝l/2，匀角速度为，求绳子的张力、铰链A的约束力及轴承O、D的附加动约束力。FOy＝mg附加动约束力以整体为研究对象 例12在悬臂梁AB的B端装有质量为mB、半径为r的均质鼓轮，如图示，一主动力偶，其矩为M，作用于鼓轮以提升质量为mC的物体。设AB=l，梁和绳子的自重都略去不计。求A处的约束力。解：研究鼓轮及物块mca根据达朗贝尔原理a鼓轮角加速度为=a/r，惯性力分别为?鼓轮及物块mc受力图整体受力图? 例12在悬臂梁AB的B端装有质量为mB、半径为r的均质鼓轮，如图示，一主动力偶，其矩为M，作用于鼓轮以提升质量为mC的物体。设AB=l，梁和绳子的自重都略去不计。求A处的约束力。研究整体 aAτaAτacAFmgFgcyFgcxMgc惯性力?受力图?例13：运动分析：平衡方程： 例题14匀质细杆悬挂如图，已知：杆的质量为m，长为2L，绳长为L，在运动过程中，绳始终张紧，并且A端以匀速率运动。试用动静法求在图示位置时，作用在杆上的力偶矩M的大小及两绳的张力。 加惯性力，作受力图TAMTBcmgFgcxFgcyMgcAB匀质细杆悬挂如图，已知：杆的质量为m，长为2L，绳长为L，在运动过程中，绳始终张紧，并且A端以匀速率运动。试用动静法求在图示位置时，作用在杆上的力偶矩M的大小及两绳的张力。 vBPωaAεaBnaBtaAaBAtaBAnaAaCAtaCAn运动分析确定aC、ε确定惯性力1.以A为基点研究B,确定ε2.以A为基点研究C,确定aC vBPω运动分析以A为基点研究B（逆时针）以A为基点研究CaAεaBnaBtaAaBAtaBAnaAaCAtaCAn 加惯性力，作受力图TAMTBcmgFgcxFgcyMgcAB（逆时针）P列平衡方程，求未知力：aAεaBnaBtaAaBAtaBAnaAaCAtaCAn 在图示系统中，已知：匀质圆盘重为Q，半径为R，平板重为P，圆盘与平板间无相对滑动，板放在的光滑斜面上，圆盘与的斜面之间有滑动，其动滑动摩擦系数为。试求：（1）圆盘的角加速度；（2）平板沿斜面即将脱离圆盘时的速度，若系统在AC=L位置由静止开始进入运动。例题15 运动分析：板AC：平动圆盘O：定轴转动εa受力分析：QPMgOFgNANBFBQMgOFBNBFCNC对于整个系统：平面一般力系，三个独立平衡方程，四个未知数:ε、NB(或FB)、NA、NA的作用点。在图示系统中，已知：匀质圆盘重为Q，半径为R，平板重为P，圆盘与平板间无相对滑动，板放在的光滑斜面上，圆盘与的斜面之间有滑动，其动滑动摩擦系数为。试求：（1）圆盘的角加速度；（2）平板沿斜面即将脱离圆盘时的速度，若系统在AC=L位置由静止开始进入运动。 解：系统圆盘QPMgOFgxNAFBQMgOFBNBFCNCNB 1.运动分析：2.受力分析：例题16aC附加动反力。 DE受力分析：BDCm1gmgFEYFEXFgC2MgC2FBYFBXFDYFDXFDYFDXDE杆：BD杆：附加动反力。 BAMG运动分析加惯性力、作受力图例题17aAB BAMGQ1Q2PYAXAMgAFgQ2MgBFgPaAB 真题（2011）图示匀质圆环在铅垂面内。已知:圆环质量为m、半径为R，试用动静法求当截断绳O2B的瞬时，圆环质心C的加速度。αaCxaCyMITFICyFICxmg运动分析受力分析aAaCAaCyaCx 真题（2011）图示质量为m、半径为R匀质圆盘可绕O转动。已知:OB=L，圆盘初始静止，试用动静法求撤去B处约束瞬时，圆盘质心C的加速度和O处约束力。αaC运动分析受力分析MIFOyFICmgFOx 讨论作业：重点：运动学分析，加惯性力。 例6在图示机构中，沿斜面向上作纯滚动的圆柱体和鼓轮O均为均质物体，各重为P和Q，半径均为R，绳子不可伸长，其质量不计，斜面倾角，如在鼓轮上作用一常力偶矩M，试求：圆柱体A的角加速度。拓展：?虚位移原理求解