达朗贝尔公式、波的传播 27页

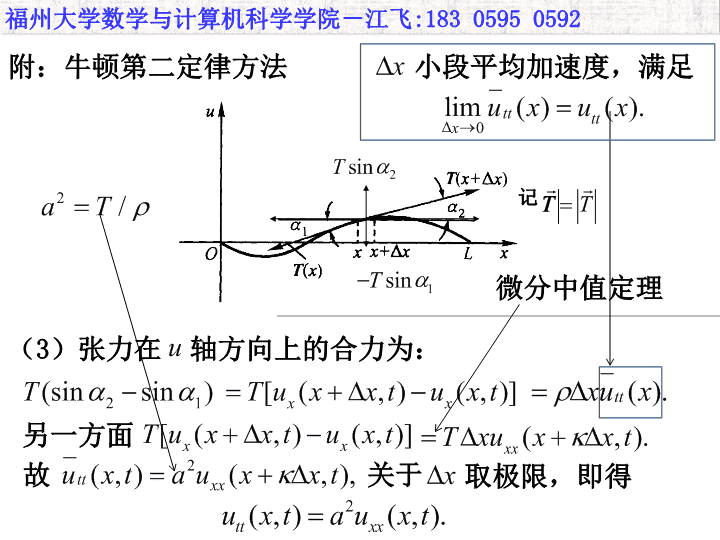
福州大学数学与计算机科学学院－江飞:18305950592记记（3）张力在　轴方向上的合力为：另一方面附：牛顿第二定律方法故关于取极限，即得小段平均加速度，满足微分中值定理 1.叠加原理（思想：化繁为简，大道至简）§2达朗贝尔（d’Alembert）公式、波的传播福州大学数学与计算机科学学院－江飞:18305950592*物理上叠加现象：几种不同原因的综合所产生的效果等于这些不同原因单独（假设其他原因不存在）产生的效果的累加。比如，声学中把弦线振动时所发出的复杂的声音分解成各种单音的叠加（类比：三原色）。它对于用线性方程和线性定解条件描述的物理现象来说，都是成立的。例如：若　　　　是方程　　　　　　　　　　的解，而　　　　是方程　　　　　　　　　　的解，则对于任意的常数　　、　，函数是方程的解。 2.弦振动方程的达朗贝尔解法（理想化研究）*理想化假设：考察边界的影响可以忽略不计的情况，或考察的弦线长度很长，而我们所关注的又只是在较短时间内且距离边界较远的一段范围中的运动情况，那么边界条件的影响就可以忽略，并不妨把所考察的物体的长度视为无限长。这样的情况下，定解问题归结为如下形式该定解问题的定解条件只有初始条件，故柯西（Cauchy）问题（或初值问题）。相应地，定解问题中既有初始条件，又有边界条件，则称为初边值问题。外力为零时，称为自由振动，否则称之为强迫振动。 这样求解弦振动的柯西问题就转化为分别求解齐次方程带非齐次边界条件的柯西问题(I)和非齐次方程带齐次初始条件的柯西问题(II)柯西问题自由振动零初始条件受迫振动利用叠加原理，进行半齐次化 *下面用自变量变换的方法求解自由振动情况的柯西问题(I)(2.1)柯西问题(I)类似地，从而，方程(2.1)就化为引入新自变量：。利用复合函数求导的法则，有 关于积分一次，可得结果，我们从弦振动方程就推导其通解再关于积分一次，就可以得到它的通解下面我们来确定　和函数表达式。显然属于可微函数时，必有 把上述通解表达式代入初始条件，得到：对（2.3）进行积分，可得（2.2）（2.3）（2.4）联立（2.2）和（2.4），可得 故定理2.1设振动的柯西问题(I)存在唯一的解　　　，它由达朗贝尔公式出：，那么自由注：柯西问题(I)的解关于初始条件的连续依赖性（稳定性）也可以很容易地从达朗贝尔公式中看出。 事实上，令任意则且与的表达式相减，并对所得等式两边取绝对值，最后对右边用三角不等式，可得故在有限时间内，自由振动的解　关于初始值连续依赖。 3.传播波*考察　　　　　　　　　情况：：波速。由左图可知振动的波形以常速度　向右传播。因此，　　　的所描述的运动规律称为右传播波，同样形如　　　　的解称为左传播波。问题（I）的解表示为右传播波和左传播波相叠加的方法，称为传播波法（行波法）。 4.依赖区间、决定区域和影响区域*依赖区间：点　　　处的值　　　由初始条件　　　和　　　在　轴的区间　　　　　　　上的值所唯一确定,而与　　　和　　　在该区间以外的值无关。这个区间称为点　　　的依赖区间。斜率：斜率： *决定区域：斜率：斜率：交点：这个三角形区域内任意一点的依赖区间都在区间内部，因此，解在此三角形区域内部的数值完全由区间　　　上的初始条件决定，与该区间外的初始条件无关。这个三角形区域称为区间　　　的决定区域。 *影响区域：斜率：斜率：如果区间收缩为一点，那么就得到了点的影响区域。有变动(初始扰动)。那么，经过时间后该扰动所影响到的范围就由不等式时，初始条件　　和的值在区间上所限定，而在此范围外的区域则感受不到区间上初始影响。上式所表示的区域称为区间的影响区域。 *特征线：我们看到，扰动的实际上沿特征线往外传播。扰动以有限速率传播，是弦振动方程的一个重要特点。斜率：斜率： 例题：利用行波法来讨论一端固定的半无界弦的自由振动问题（自由振动Piston问题）解：设想在　　　的左侧仍然有弦存在,并在振动过程中　　点始终不动。问题于是转化为：如何将上已知的初始函数延拓为整个直线　上的函数，并使得用延拓后的函数作初值的柯西问题的解在　　　点恒为零。为此，记　　　及　　　是由　　和分别延拓而得到的函数。由达朗贝尔公式，以及为初值的柯西问题的解为 要使在点恒为零，就应当成立为此只需要将和分别作奇延拓:则当时， 综上即知，自由振动Piston问题的解为而当时，注意到p16:3 5.齐次化原理（Duhamel原理）现在我们考察零初值条件强迫振动情形的初值问题柯西问题(II)外力离散化利用叠加原理分解则冲量定理：外力与速度关系切割无限加密加细 注意到表示在时间段，弦才受到外力作用（可以认为是瞬时外力）。因此单位长度的弦受到的冲量，其引起的对应的处单位另一方面表示时刻　时在处长度的弦的动量改变量近为，由冲量定理知问题（III）问题（1）可近似替换成 如果记，则为如下齐次方程的定解问题的解于是记上述问题的解为应表示为按照叠加原理，柯西问题(II)的解 定理2.2(齐次化原理)若　是下列问题的解(其中是参数)，则柯西问题(II)的解可以表示为问题(III)下面求　　　　　的表达式，在(III)中作变换则满足 利用达朗贝尔公式求出上述初值问题(I)的解为再代入(2.5)式就得到初值问题(II)的解(2.5) 上面我们通过对物理模型的分析，应用叠加原理，得出了定解问题(II)的解的表达式。它究竟是否确实为定解问题(II)的解，还需要按照解的定义进行数学上的验证。区域　为　　　平面上过点　　　向下作两特征线与轴所夹的三角形区域，见右图。 设　　　，利用含参变量积分的求导法则，可得 故 p.17:8 假设抽象柯西问题有解，则该问题可定义一个解算子附：抽象版本齐化原理（半群理论）线性微分算子解算子则利用齐次化原理，可得　　　　　　　的解为故　　　　　　　的解为比如：的解为回忆常数变易法