13 达朗贝尔原理 15页

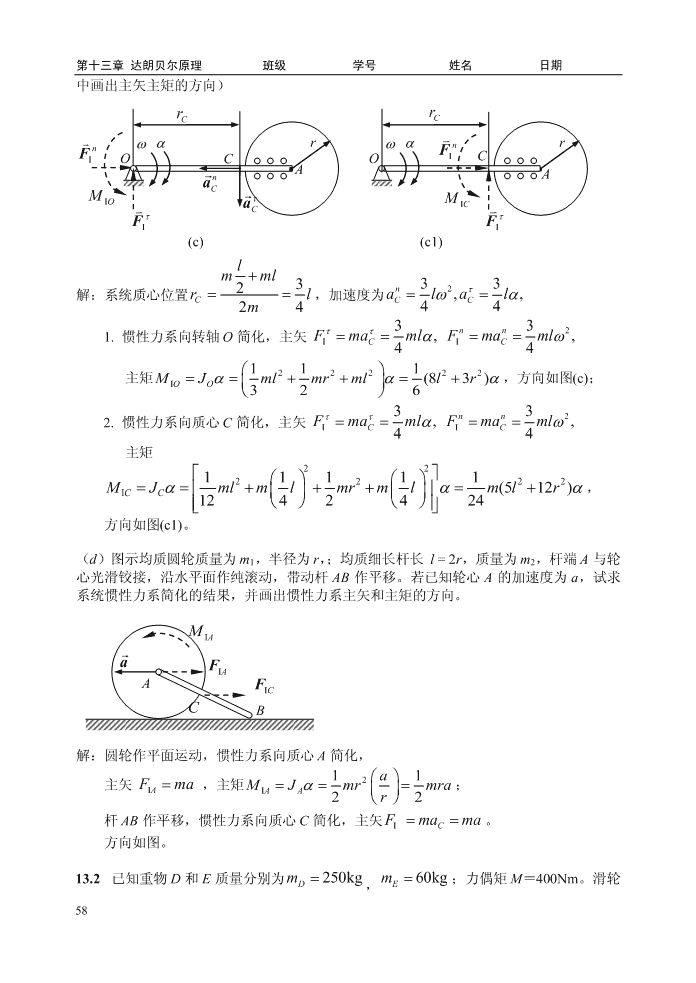
第十三章达朗贝尔原理班级学号姓名日期十三、达朗贝尔原理13.1求下列刚体惯性力系简化结果。（a）质量为m，半径为r的均质圆盘绕水平轴O作定轴转动，角速度为，角加速度为，试求圆盘的惯性力系向转轴O简化的结果。（在图中画出主矢主矩的方向）rnOnrOFIFIaC.nCFCIaCMMIOICFI(a)(a1)nn2解：1.惯性力系向转轴O简化，主矢Fmamr,,FmamrIICC32主矩MJmr，方向如图(a)；IOO2nn22.惯性力系向质心C简化，主矢Fmamr,,FmamrIICC12主矩MJmr，方向如图(a1)。ICC2(b)均质杆OA质量为m，长为l，可绕O轴转动。图示瞬时，角速度为零，角加速度为，试分别求该瞬时杆的惯性力系简化的结果（1）向转轴O简化；（2）向质心C简化。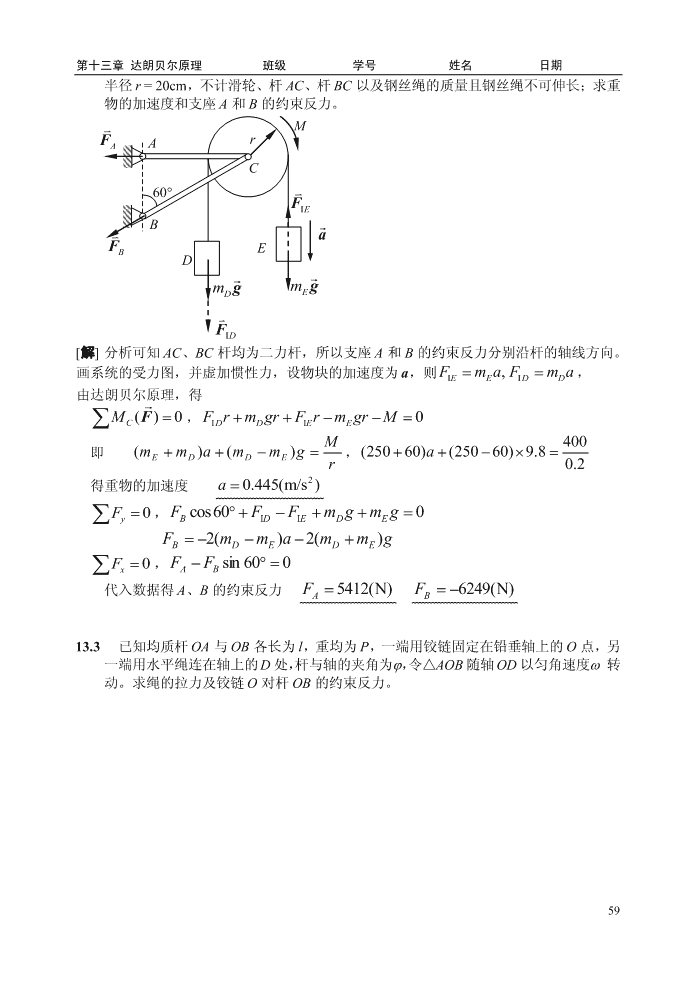（在图中画出主矢主矩的方向）CCOOAAMaMIOFCICFII(b)(b1)1解：1.惯性力系向转轴O简化，主矢FImaCml,212主矩MJml，方向如图(b)；IOO312.惯性力系向质心C简化，主矢Fmaml,IC212主矩MJml，方向如图(b1)；ICC12（c）质量为m，长为l的均质杆杆端与质量为m、半径为r的均质圆盘中心固结，绕水平轴O的作定轴转动，角速度为，角加速度为，试求系统惯性力系简化的结果（在图57 第十三章达朗贝尔原理班级学号姓名日期中画出主矢主矩的方向）rCrCrnrFnFIOCOICnAAaCMIOaMICCFFII(c)(c1)lmml23n332解：系统质心位置rl，加速度为al,,alCCC24m443nn321.惯性力系向转轴O简化，主矢Fmaml,Fmaml,ICIC4412122122主矩MJmlmrml(8l3)r，方向如图(c)；IOO3263nn322.惯性力系向质心C简化，主矢Fmaml,Fmaml,ICIC44主矩22121121122MJmlmlmrmlml(512)r，ICC1242424方向如图(c1)。（d）图示均质圆轮质量为m1，半径为r，；均质细长杆长l=2r，质量为m2，杆端A与轮心光滑铰接，沿水平面作纯滚动，带动杆AB作平移。若已知轮心A的加速度为a，试求系统惯性力系简化的结果，并画出惯性力系主矢和主矩的方向。MIAaFIAAFICCB解：圆轮作平面运动，惯性力系向质心A简化，112a主矢FIAma，主矩MIAAJmrmra；22r杆AB作平移，惯性力系向质心C简化，主矢Fmama。IC方向如图。13.2已知重物D和E质量分别为m250kgm60kg；力偶矩M＝400Nm。滑轮D，E58 第十三章达朗贝尔原理班级学号姓名日期半径r=20cm，不计滑轮、杆AC、杆BC以及钢丝绳的质量且钢丝绳不可伸长；求重物的加速度和支座A和B的约束反力。MFAArC60FIEBaFBEDmDgmEgFID[解]分析可知AC、BC杆均为二力杆，所以支座A和B的约束反力分别沿杆的轴线方向。画系统的受力图，并虚加惯性力，设物块的加速度为a，则FmaF,ma，IIEEDD由达朗贝尔原理，得MC()F0，FrmgrFrmgrMIIDDEE0M400即(mEmD)a(mDmE)g，(25060)a(25060)9.8r0.22得重物的加速度a0.445(m/s)Fy0，FBcos60FIDFIEmDgmEg0F2(mm)a2(mm)gBDEDEFx0，FAFBsin600代入数据得A、B的约束反力F5412(N)F6249(N)AB13.3已知均质杆OA与OB各长为l，重均为P，一端用铰链固定在铅垂轴上的O点，另一端用水平绳连在轴上的D处，杆与轴的夹角为，令△AOB随轴OD以匀角速度转动。求绳的拉力及铰链O对杆OB的约束反力。59 第十三章达朗贝尔原理班级学号姓名日期ADBFTBECFIFOyPOOFOx[解]OB杆作定轴转动，其惯性力为沿杆方向线性分布，受力如图。线性分布的惯性1lPl2力系的合力过E点，且BEOB，Fmasin。IC33g22llMO()F0，FlTIcosFcosPsin0322l1FP(sintan)T32gFx0，FOxFITF021lFFF(tansin)POxTI26gFy0，FPOy0FPOy13.4均质长方体浪木重为P，悬挂在两根等长的软绳上，OO1＝AB，从＝30的位置无初速释放开始摆动；求在下面两个瞬时浪木的加速度和两绳的拉力：(1)开始运动瞬时；(2)浪木通过最低位置瞬时。OO1OO1nnFnFT1FInFT2T1aFCFT2BIBCA0.2mACABaAFaaIC2mPCP(c)(a)(b)[解]（1）初瞬时浪木受力如图(b)，60 第十三章达朗贝尔原理班级学号姓名日期P∵浪木平动且初瞬时各点速度v0，∴aaAO，FaCAICg1F0，PsinFI0，agC2Fn0，FT1FT2Pcos0MC(F)0，FFT1(1cos300.1sin30)T2(0.1sin301cos30)01联立求解得初瞬时浪木的加速度ag；C2两绳的拉力FP0.408；FP0.458T1T2（2）浪木于初始位置平移至最低位置过程，由动能定理得1P22v0Pl(1cos)，得v2(1cos)glCC2g最低位置处，受力如图(c)，2PnvCF0，FI0即aC0得aCCa2(1cos)ggl或ag(23)CMC(F)0，FFT11T210nFn0，FT1FT2FIP011nnPFF(FP)(aP)T1T2IC22gFF0.628PT1T213.5图示长a=20cm，宽b=15cm的均质矩形板质量为27kg，由销A、销B悬挂，如果突然撤去销B，求该瞬时矩形板的角加速度和销A的约束反力。FAyFAyMIAFAxAABBFAxFIFICCbbMICamgamgCCaa(a)(b)61 第十三章达朗贝尔原理班级学号姓名日期22ab[解1]撤去销子的瞬时，0，矩形板将作定轴转动，a惯性力系向C2，22ab转轴A简化FF即Fmam；IIIC2222MJ11ma(2b2)mabma(2b2)IAA1223ba矩形板受力如图(a)，图中sin，cos2222abab由达朗贝尔原理，得aa122MA()F0，MIAmg0，mgma(b)022322abbFx0，FFAxIsin0，FmAx02ab2222abaFy0，FAyFIcosmg0，FAymmg02ab223gaba解得22，FmAx，FAymgm2(ab)222代入数据得矩形板的角加速度47.07rad/s销A的约束反力F95.32NF137.67NAxAy22ab[解2]撤去销子的瞬时，0，矩形板将作定轴转动，a惯性力系向C2，22ab122质心简化FIFI即FImaCm；MICCJma()b212ba矩形板受力如图(b)，图中sin，cos2222abab由达朗贝尔原理，得aMA()F0，mgMIICFAC0，22222a122ababmgma(b)m02122222abbFx0，FFAxIsin0，FmAx02ab2262 第十三章达朗贝尔原理班级学号姓名日期22abaFy0，FAyFIcosmg0，FAymmg02ab223gaba解得22，FmAx，FAymgm2(ab)222代入数据得矩形板的角加速度47.07rad/s销A的约束反力F95.32NF137.67NAxAy13.6图示涡轮机的转盘重P＝2kN，重心C到转轴z的距离e＝0.5mm（图中已夸大），转轴z垂直于转盘的对称面，盘匀速转动，转速n＝6000rpm，AB＝h＝1000mm；求当转盘转到重心C位于yz平面的瞬时，止推轴承A和向心轴承B的静反力和附加动反力。zBFByFBxnhC2FIFAzPhA2xFFAyyAxn6000[解]转盘作匀速定轴转动，角速度628(rad/s)，3030P222惯性力系简化为合力Fe0.000562840.2(kN)Ig9.8转盘受力如图，由达朗贝尔原理，得My()F0，FhBx0FBx0Fx0，FFAxBx0FAx0hMx()F0，FhPeFByI0，2e1FPFByIh2e1Fy0，FFAyBy0FAyPFIh2Fz0，FPAz0FPAz63 第十三章达朗贝尔原理班级学号姓名日期e最后得静反力FFP1(kN)，FP2(kN)AyByAzgh动反力FFF20.1(kN)AyByI264 第十三章达朗贝尔原理班级学号姓名日期13.7已知均质杆AB重为P，以两根与之等长的绳子悬挂在水平位置；求B端绳子突然断开瞬时A端绳子的拉力。O1O2FIyMFICTxCACaABxABaAFIxPaCA（a）yy（a1）[解]（1）在B端绳子突然断开瞬时，杆的角速度及杆上各点的速度均为零，A点轨迹为以O1为圆心、绳长为半径的圆周，则aAOA1nn1杆将作平面运动，由基点法aaaa，aa0,l，CACACACACA2laa，aaCxACyCA2运动分析如图(a1)，受力分析如图(a)，（设杆长为l，此瞬时杆的角加速度为，）虚2PlPPl加惯性力系MJ；Fmaa，FmaICCIxCxAIyCy12ggg2由达朗贝尔原理，得PaA0ga0FF0,0AxxIPl3gFyy0,PFTIF0PFT0，解得2g2llM()F0,FM0lPl21CCTIFP2FT0T212g4P即：B端绳子突然断开瞬时A端绳子的拉力FT4（2）65 第十三章达朗贝尔原理班级学号姓名日期OOFI2FTM60ICACBACBaAaFAPI1aCA（b）（b1）在B端绳子突然断开瞬时，杆的角速度及杆上各点的速度均为零，A点轨迹为以O为圆心、绳长为半径的圆周，则aOA，杆将作平面运动，Ann1由基点法aaaa，aa0,l，aaa，CACACACACA2CACA2PPlPl惯性力系主矢分量FFmaa,ma，主矩M，I1AAI2CAICgg212g方向如图。由达朗贝尔原理，得1F0,FTFI2sin60Psin600FTmlsin60Psin6002l，MCC()F0,FTIsin60M0Flsin601ml202T21218g23解得，B端绳子突然断开瞬时A端绳子的拉力为FPT13l1313.8已知圆轮重G、半径为R，沿水平面纯滚。若不计滚阻：试问在下列两种情况下，轮心的加速度及接触面的摩擦力是否相等：(1)在轮上作用一矩为M的顺钟向力偶；(2)在轮心上作用一水平向右、大小为M／R的力P。MICMMFICCGGFfF(1)N(1)-a[解]（1）轮作纯滚动，设轮心加速度为a，角加速度为，则aR，G1G2GR轮受力如图，惯性力系主矢Fa，主矩MJRaIICCg2g2g66 第十三章达朗贝尔原理班级学号姓名日期由达朗贝尔原理，得MC()F0，MMIfCFR0Fx0，FFfI02Mg2M联立解得a，Ff3GR3RMICCPFICPGGF(2)fFN(2)-a（2）Fx0，PFIfF0而PM/RMC()F0，MIfCFR02MgM联立解得a，Ff3GR3R可见，(1)、(2)两种情况下，轮心加速度相等，而接触面的摩擦力不相等。13.9已知砂轮I质量m1=1kg，偏心距e1=0.5mm，砂轮II质量m2=0.5kg，偏心距e2=1mm。电动转子III质量m3=8kg，转速n=3000r/min。求转动时轴承A、B的附加动反力。ⅠFI2ⅢBAe2e1ⅡFI1FNBFNA10050200502n23000[解]砂轮角速度100(rad/s)6060砂轮I、II的惯性力分别为2322Fme10.510(100)5(N)，I1112322Fme0.5110(100)5(N)I222当只求动反力时，受力图中重力可不考虑，由达朗贝尔原理67 第十三章达朗贝尔原理班级学号姓名日期MAF0，200FNB250FI150FI20MBF0，200FNA250FI250FI10解出附加动反力FF73.5(N)NBNA即：转动时轴承A处的附加动反力为73.5N，方向与图示相反；B处的附加动反力为73.5N，方向与图示相同。13.10图示绕线轮重P，半径为R及r，对水平质心C的转动惯量为J，在与水平成C角的常力F作用下纯滚动。试求（1）轮心加速度；（2）绕线轮作纯滚动的条件。TMICRCaCFTFICrPFfFNP[解]研究绕线轮，受力如图，惯性力系主矢Fa，主矩MJICCICCg绕线轮纯滚动时有aR，由达朗贝尔原理，CFx0，FTcosFICFf0Fy0，FNFTsinP0MCF0，FrFRMTfIC0PF(RrJcos)TCFTR(Rcosr)g联立解得a；FCfP2P2JCRJRCgg及FPFsin，再将F、F代入FfFNTNffNPF(RrJcos)TCg得绕线轮作纯滚动的条件为fg）P2(PFsin)(JR)TCg68 第十三章达朗贝尔原理班级学号姓名日期13.11如图所示，质量为m、倾角为的三棱柱与水平面的摩擦不计；质量为m、12半径为r的均质圆柱沿三棱柱斜面向下作纯滚动，求三棱柱的加速度及圆柱中心相对于三棱柱的加速度。aFIrMIOeOOFIearFIrMIOmgOaa2FAAFIefaFDm1gIAmg2FN1()aFN()b()c[解]取圆柱中心为动点，三棱柱为动系，由加速度合成定理aaaaer式中aa为圆柱中心的加速度，aa为三棱柱平动的加速度，a为圆柱中心aOerar相对于三棱柱的加速度，圆柱角加速度，加速度如图(a)，系统的受力图及虚加惯r性力系如图(b)，圆柱的受力图如图(c)，112其中Fma，Fma，Fma，MmrmraI1AeI2eeI2rrIOr2222由达朗贝尔原理，研究系统，Fx0，FIAFIrcosFIe0研究圆柱，MD0,MIOFrFrIrIecosmgr2sin0代入惯性力表达式，得mamacosma01e2r2e1mramarmarcosmgrsin02r2r2e22mgsin22联立解得三棱柱的加速度为a，e23(mm)2mcos1222(mmg)sin12圆柱中心相对于三棱柱的加速度为ar23(mm)2mcos12213.12图示均质圆盘以等角速度绕z轴转动，圆盘平面与转轴z交成角，轴承A和B与圆盘中心相距各为a和b；圆盘半径为R，质量为m，厚度可忽略不计。求两轴承A和B的附加动反力。69 第十三章达朗贝尔原理班级学号姓名日期zBzFByFBxy"byCMIyaMIxxFAzxFAyAFAx[解]在图示坐标系中，由于圆盘上各点的x坐标对于z轴对称，圆盘的惯性积Jxzmixizi0为计算J作圆盘的中心惯性主轴oxyz如图yzJyzmyziiimyi(cosizisin)(sinyizicos)m2JxcossinRsin28以圆盘和轴为研究对象，受力图中惯性力向中心点O简化结果为P2m222Fa0MJRsin2，MJ0ICIxyzIyxzg8由达朗贝尔原理，得Fx0FAxFBx0Fy0FAyFBy0Fz0FAz0MxF0MIxaFAybFBy0MyF0MIyaFAxbFBx022mR联立解得FFF0；FFsin2AxBxAzAyBy8(ab)70 第十三章达朗贝尔原理班级学号姓名日期13.13均质细杆OA、AB的质量均为m、长均为l，用光滑铰链O、A连接如图。初始时两杆均处于水平位置，求系统由静止释放瞬时，两杆的角加速度。FI1FI2FI2FOCABAxAC2BFC2Ox1FMmgOyMmg1Mmg2FIC2IC1IC2Ay解：系统静止释放瞬时，两杆的角速度均为零，OA杆将作定轴转动，AB杆作平面运动。设角加速度分别为1、2n由刚体平面运动基点法，aaaa，式中C2ACA22CAn11a0，al所以al()C2AC2A22C2122112对系统虚加惯性力Fml，Mml，I11IC11212112Fml()，MmlI212IC22212根据达朗贝尔原理，121ll对AB杆MA()F0，ml2ml(12)mg0…..…..(a)12222对系统MO()F0，121ll1213l3lmlmlmgmlml()mg0(b)1121212222122229g3g联立(a)、(b)，解得,127l7l71