三维多向编织复合材料有效弹性模量的细观计算力学分析 4页

第18卷第2期计算力学学报Vo1．18No．22001年5月CHINESEJOURNALOFCOMPUTATIONALMECHANICSMav2001文章编号：1007—4708(2001)02—0231一O4三维多向编织复合材料有效弹性模量的细观计算力学分析庞宝君，曾涛，杜善义(哈承滨工业大学复合材料研究所-啃笨蒺150001)摘要：编织复台材料性能预报与材料优化设计研究是编织复告材料研制开发的重要环节。本文在已建立的三维多向编织复音材料单胞几何模型的基础上，研究建立了含多相介质单元曲有限元舟析方法结合实例预报了碳／环氧四向编织复合材料的有鼓性能井和实验结果进行了对比。关键词：骗织复合材料；细观计算力学；力学性能中国分类号：O34文献标识码：A型；Hatta的等效夹杂法本文在已建立的三维多向编织复合材料单胞几三维编织结构复合材料是近年来迅速发展起来何模型的基础上．研究建立了含多相介质单元的有限元分析方法结合实例预报了碳／环氧四向编织复的结构复合材料．其最突出的特点是整体性好，力学合材料的有效性能并和实验结果进行了对比，吻合结构合理．克服了传绕层合复合材料的一些弱点t为较好为进一步研究三维多向编织复合材料的车构复合材料应用于航空、航天等高科技领域提供了广关系非线性行为及其细观损伤机理奠定了基础。阔的前景。细观力学将复合材料作为结构来分析，从而可以有效地参与复合材料的性能预报及其优化设2复合材料单胞有限元模型计。对于三维多向编织复合材料．由于其相几何的复杂性，使得其力学性能的细观力学分析既具有工程根据本文作者在文献[5，6]中所建立的三维多意义卫具有学术价值向编织复合材料单胞几何模型，可以进一步建立有关于编织复合材料力学性能的研究感性多于理限元分析模型。以四向编织复合材料为例．在复合材性，实验研究多于理论研究。有代表性的研究工作主料分析单胞几何模型的基础上，采用规则的八节点要有：WhiteneyC等基于=维层舍板理论的分析模体单元对其整个单胞进行剖分，其有限元同格如图型；YangC等的纤维偏斜模型；Ma构造的力学模1所示。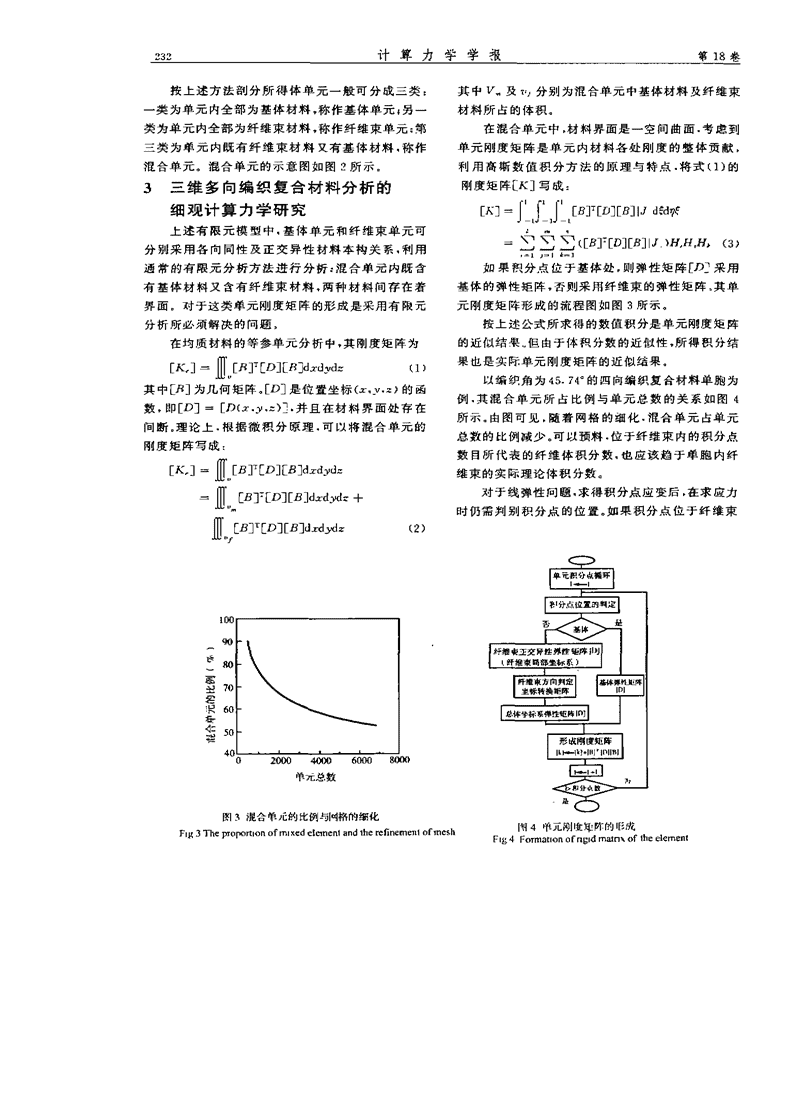Il彳j限元网辛}}丹图[制2滩☆单元惑图Fig2TemixedelememFigIThefiniteelem~mmesh收稿日期11999—05—31修改稿收到日期2000—11-28基金项目：国家自然科学基金(19932030)，作者简介鹿宝君<1963一)．男-博士．教授· 计算力学学报第18卷按上述方法剖分所得体单元一般可分成三类：其中及，分别为混合单元中基体材料及纤维柬一类为单元内全部为基体材料，称作基体单元·另一材料所占的体积类为单元内全部为纤维束材料，称作纤维柬单元；第在混合单元中，材料界面是一空间曲面．考虑到三类为单元内既有纤维束材料又有基体材料，称作单元刚度矩阵是单元内材料各处剐度的整体贡献，混合单元。混台单元的示意图如图2所示。利用高斯数值积分方法的原理与特点．将式(1)的3三维多向编织复合材料分析的刚度矩阵[K]写成：细观计算力学研究[]=』f』[且]丁[D][且]ld翱上述有限元模型中，基体单元和纤维柬单元可=∑∑∑([盯[D][础J)H(3分别采用各向同性及正交异性材料本构关系，利用-1J—lk-】通常的有限元分析方法进行分析混台单元内既古如果积分点位于基体姓，则弹性矩阵[．f)栗用有基体材料又古有纤维束材料，两种材料间存在着基体的弹性矩阵，否则采用纤维柬的弹性矩砗其单界面。对于这类单元刚度矩阵的形成是采用有限元元刚度矩阵形成的流程图如图3所示。分析所必须解决的问题按上述公式所求得的数值积分是单元刚度矩砗在均质材料的等参单元分析中，其刚度矩阵为的近似结泉。但由于体积分数的近似性，所得积分结胛果也是实际单元刚度矩阵的近似结果。[K，]=⋯]T[D]EB]dxdydz(1)以编织角为45．7的四向编织复台材料单胞为其中[]为几何矩阵。[D]是位置坐标，．)的函例，其混合单元所占比例与单元总数的关系如图4数，即[D]=[D(．Y，z)．并且在材料界面姓存在所示由图可见，随着网格的细化．混台单元占单元间断。理论上．根据微积分原理，可以将混台单元的总数的比例减少。可以预料．位于纤维束内的积分点雕度矩砗写成：数目所代表的纤维体积分数，也应该趋于单胞内纤胛[K，]=“⋯p][D][B]dxdydz维柬的实际理论体积分数胛=对于线弹性间题，求得积分点应变后，在求应力⋯]：[D][B]dxdydz+时仍需判别积分点的位置。如果积分点位于纤维束胛⋯][D][B]dxd(2)一一露￡番：垄单兀总数图3混合单元的比例与H杆的缩化『斟4单元剐噬垭阵的JB成Fig3ThepToportionofmixed~lemenlandlherefinemenlofmeshFig4Formationofngidmalrixoflheelemenl 第2船鹿宝君等：三维多向编织复合材料有效弹性模量的细观计算力学分析2S3上，则采用纤维束的弹性矩阵，否则采用基体的弹性围5为不同编织角的杨氏弹性模量实验-与理矩阵。论预报的对比固。由实验结果可见，由拉伸实验与压按复合材料的有效模量理论]，在复合材料单缩实验所涮杨氏弹性模量均分布在一个带型区域胞上加入均匀边界条件，使得在统计材料内产生统内，随编织角的增加，纵向杨氏弹性模量递减。由图计均匀场。求得材料单胞的应力、应变场后，按体积可见，尽管实验点分散较大，但本文所建立的有限元平均原则计算平均应力和平均应变，继而求出复合法对臣、的预报结果吻合较好，井与等效夹杂甚材料的有效模量。理论预报曲线有相同的变化趋势实验点的分散根据以上分析方法，利用FORTRAN语言，编可能与编织复合材料试样材质本身的分散、试件的铽了适合于解决三维多向编织复合材料力学性能的装卡对中、测量的误差等因素有关。横向杨氏弹性模细观计算力学的有限元分析软件。量是通过压缩实验进行的，实验点与本文的有限元方法及等效夹杂洼预报结果均吻合较好。4四向编织复台材料弹性模量算例4．3计算收敛住讨论4．1组分材料的性能参数关于本文所建立有限元分析方法的计算收敛性算例以天津纺织工学院研制的碳／环氧四向编间胚，以上例中编织角=4884。的纵向杨氏弹性织复合材料为对象，基体材料为TDE一85环氧树模量臣分析为例，其分斩结果如图6所示。由围可脂，增强纤维为T300碳纤维，纤维柬规格为12K。将见，当单元数较小时，纵向杨氏弹性模量E工的计算纤维柬看作是碳纤维增强的环氧基单向复合材料-值波动较大，随着单元数的增加，其计算值药于稳纤维柬和基体作为四向编织复合材料的组分，其性定。可见，其收敛性是能够得到保证的。§一：々自n能参数如表1所示(表中L表示纤维束纵向，T为横5结论向)。表1单向纤维束和纯树脂性能本文针对三维多向编织复合材料单胞相几何的Tand1Materialpropertiesofunidirectional复杂性，建立了包古两种介质单元即所谓混合单元fiberrodandpureresinE、G；GPa的剐度矩阵分析方法以碳／环氧四向编织复合材料单向碳／环氧f纯树腊为例对其有效弹性模量进行了预报，所预报的结果丘；E丁1G。rrJl‰j‰与实验吻合较好，证明了该方法的有效性。同时，可173．581l0．7418．78仉320．{1l432l0．37I57．8进一步发展使其应用于该类复合材料的本构关系4．2四向编织复合材料性能预报结果非线性及其损伤机理分析中0一最皇盛SumofElementsN5畅氏i制幢±i6计箅结果收敛Fig．5Young"smodulusFig：6Convergenceofcalculatedvalue 计算力学学报第18卷ofTechnology，1996—28(6){1—6)．参考文献(References)[63鹿宝君，杜善义，等．三维四向编织复合材料[1]WhitneyTJ，ChouTW．Modelingof3-D细观组织厦分析模型[J]．复合材料学报．Angle—InterlockTextileStructuralComposite1999，16(3)：133·139．(PangBa0一iun，DuShan—yi．Meso—structureandmodelingofth-口]．JCompMater，1989，23：890—911．ree—dimensionalmulti-directionalcomposites[2]YangJM．MaCL，ChouTW．Fiberinclinationmodelofthree—dimensionaltextile[J]．JournalofComposites，1999，16(3)：133—139)．structuralcomposite_J]Jc唧Mat，1986，20：472-483．[7]周厦，范赋群．复合材料力学[M]．北京：高[33MaCL，YangJM，ChouTW．Elastic等教育出版社，199I．220—229．(ZhouLv，Fanstiffnessofthree—dimensionaItextilestrue—Fu—qun．MechanicsofComposites．Baijing~HigherEducationPress．1991．220—229)ruralcomposite[A]．WhitneyJM．CompositeMaterials：TestingandDesign[8]鹿宝君．三雄多向稿报复合材料力学性能预(SeventhConference)[c]．AmericanSociety报与优化谨计研究[o3．哈水溥：哈尔滨工业大学，1997-(PangBoo—iun．Theoreticalpre*forTestingMaterials，Philadelphia，1986：dictionandoptim／zatiot~ofthemechanical402-421．propertiesof3-dimensionalmultidirectional[4]HattaHElasticmodutiandthermalexp—anslontoe艏cientsofthree—dimensionalfabricbraidedcomposites[D]Harbin：HarbinInstituteofTechnology，l997)composites[J]．JournaloftheJapanSociety[9_鹿宝君．社善义，等．三雏四向碳／环氧编织复rCompositesMaterials，1988，14(2)：73—合材料实验研究．复合材料学报，1999，168O．(4)：136—141．(PangBao—iun，DuShan—yi．]鹿宝君，杜善义，等．多堆编织复合材料分析Experimentalinvestigationofthreedimensi—模型[J]．哈求滨工韭大学学掇，1996+28(6)onalfour—directionaIbraidedcarbon／epoxy1-6．(PangBoo—jun，DuShah—yi．Ananalyt—composites[J]．JournalofComposites，1999，ica[methodof3Dmuhi~lirectionallybrai~ted16(3){133—139．)compositesEJ]．JournalofHarbinInstituteMeso—-scopiccomputingmechanicsanalysisofthree’-dimensionalmulti—directionalbraidedcompositesPANGBao—jun，ZENGTao，DUShan—yi(HarbinInstituteofTechnology，Harbin150001，China)Ahstraet：Basedontheunitcellgeometricalmodelof3-dimensionalmulti~lirectiona[braidedcomposites，theforruingmethodofmulti—phaseelementstiffnessmatrixisstudied-andthemeso—scopiccalculatingmechanicsanalyzingmeth0dof3~limensionalmulti—directionalbraidedcompositesisestablished．Theeffectivemechanicalpr0perties0fthe4-directionalcarbon／epoxybraidedcompositesarepredictedandthecomparisonbetweenthetheoreticalpredictlomandtheexperimentaldataispresented．Keywords：braidedcomposites；meso·scopiccomputingmechanics；mechanicalproperties