工程力学12-1-达朗贝尔原理习题 22页

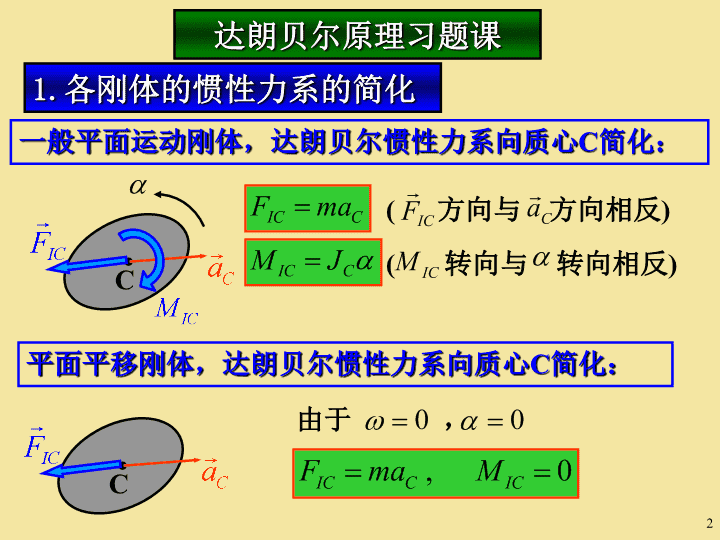
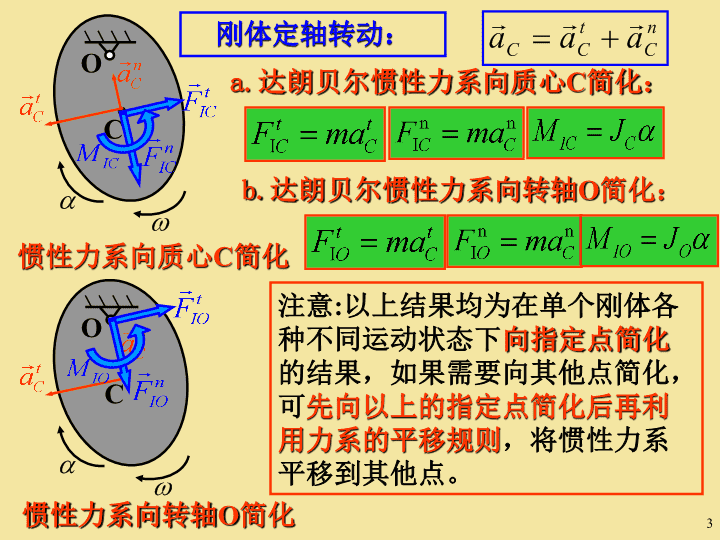
工程力学A(下)北京理工大学理学院力学系韩斌达朗贝尔原理习题课22/I 达朗贝尔原理习题课C一般平面运动刚体，达朗贝尔惯性力系向质心C简化：1.各刚体的惯性力系的简化平面平移刚体，达朗贝尔惯性力系向质心C简化：C由于，(转向与转向相反)(方向与方向相反)2 刚体定轴转动：a.达朗贝尔惯性力系向质心C简化：b.达朗贝尔惯性力系向转轴O简化：惯性力系向质心C简化OC惯性力系向转轴O简化OC注意:以上结果均为在单个刚体各种不同运动状态下向指定点简化的结果，如果需要向其他点简化，可先向以上的指定点简化后再利用力系的平移规则，将惯性力系平移到其他点。3 解：P习题21.4已知：AB杆质量m，长2l，A点速度为常矢量。求：图示位置，系统的惯性力分别向C,A两点简化的结果。BCA上式对任意角的位置成立。4 质心C点加速度分析：PBCA实际上,A点为杆的加速度瞬心5 PBCAP*实际上,,A点为杆的加速度瞬心:上式在水平方向投影:6 惯性力向C点简化：PBCP*()()()PBCP*7 惯性力若向A点简化,可把向质心C简化的惯性力和惯性力偶向A点平移：（）（）（）PBCP*PBCA8 PBCA又()已求得：另一解法：9 惯性力向C点简化：（）PBCA()()若惯性力向A点简化，将惯性力平移到A点：()()10 2.对各刚体的惯性力系进行简化前,可利用各守恒定律判断刚体的运动状态特点AB课上例题(即习题21-16)A´´由圆轮的受力,知圆轮对质心动量矩守恒:圆轮为平动!000====AAAAAAJLJLww11 yxoCBA由于，且初始根据质心运动守恒，有即质心沿铅垂线运动,故方向为铅垂方向,由C,B两点加速度关系:课上例题:12 AB杆AB长l，质量为m，圆轮半径为r，质量为m，地面光滑，杆AB从水平位置无初速释放，圆盘始终与地面接触,求杆AB运动到铅垂位置时:（1）A点的速度和AB杆的角速度。（2）A点的加速度和AB杆的角加速度。（3）地面对圆轮的约束力。习题21.1613 解：画出整体受力图和圆轮的受力图分析圆轮的受力，圆轮外力均过质心A，故圆轮对质心动量矩守恒：圆轮为平动ABC（2）当AB杆运动到铅垂时，设杆的角速度为，圆轮A点的速度为，由C，A两点速度关系ABCA´´14 由C，A两点速度关系投影：()系统整体仅受铅垂方向外力，故系统整体水平方向动量守恒：()ABCABCA´´15 ()(3)系统仅受重力，机械能守恒设点A处为势能零点，则：初始位置：杆铅垂位置：ABCABCA´´16 初始位置：杆铅垂位置：()()ABCABCA´´17 (4)取整体为对象画出受力图：由两点加速度关系：在x，y方向投影：ABCABC设杆AB的角加速度为（）轮心A加速度为()18 (5)对整体列达朗贝尔平衡方程：ABC()(1)(2)(3)(1)(2)联立得19 3.关于求解动力学问题时建立运动学补充方程的方法(1)可根据题目特点通过两点速度关系，速度瞬心法，速度投影定理，两点加速度关系，速度合成关系，加速度合成关系，角速度合成关系，角加速度合成关系等建立运动学补充方程。(2)针对某些特殊情形(如角速度等于0的时刻)也可利用加速度瞬心的概念方便地找出运动学补充方程。在“从静止释放”“静止时突然剪断”…等瞬时,有各刚体的角速度为0,此时加速度瞬心P*容易找到:此时若已知刚体上两个点的加速度方向就可确定加速度瞬心P*的位置,且刚体上各点的加速度都可由加速度瞬心确定:ABP*M20 例如:=常数,三刚体均质,质量均为m,滑道光滑,圆轮半径r,AB杆长2r,求图示瞬时滑道对滑块的约束力。P*OABCDAB杆瞬时平移:OABCD属于特殊时刻21 例如:=常数,三刚体均质,质量均为m,滑道光滑,圆轮半径r,AB杆长2r,求图示瞬时滑道对滑块的约束力P*OABCDOABCD对整体列可求画出整体受力图：22