（整理版）解答中考压轴题的“金钥匙”.doc 8页

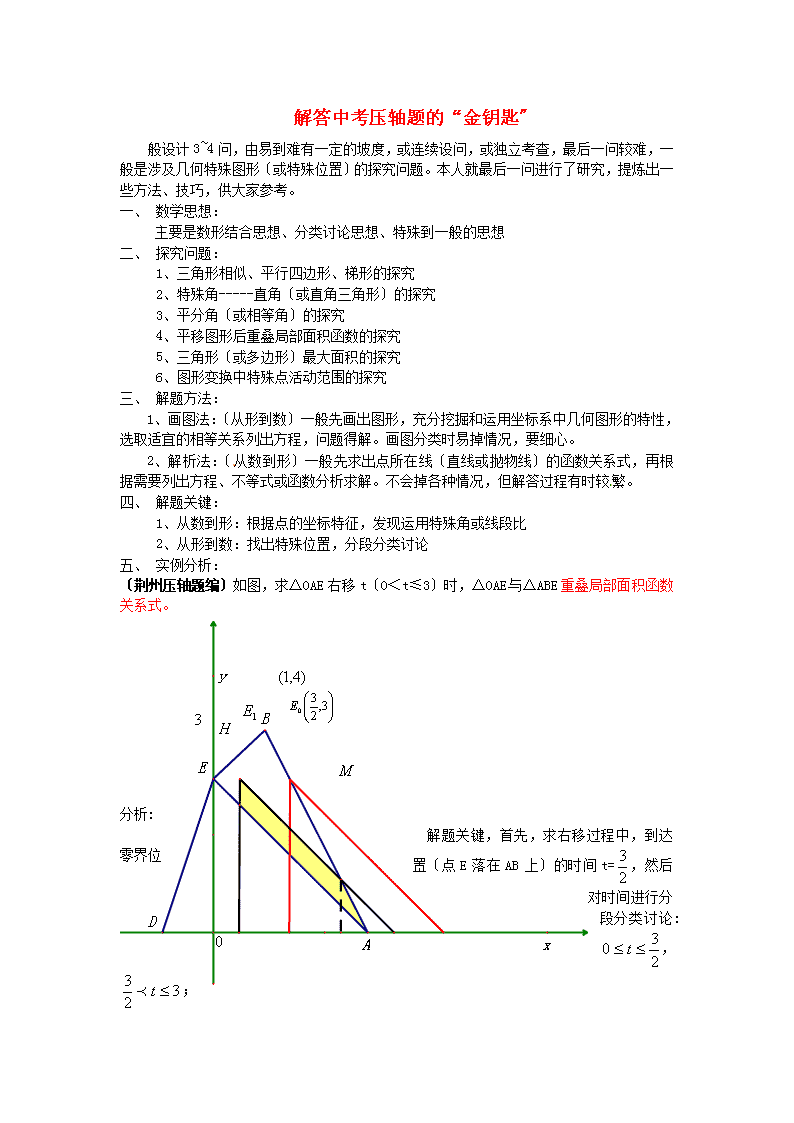
解答中考压轴题的“金钥匙〞般设计3~4问，由易到难有一定的坡度，或连续设问，或独立考查，最后一问较难，一般是涉及几何特殊图形〔或特殊位置〕的探究问题。本人就最后一问进行了研究，提炼出一些方法、技巧，供大家参考。一、数学思想：主要是数形结合思想、分类讨论思想、特殊到一般的思想二、探究问题：1、三角形相似、平行四边形、梯形的探究2、特殊角-----直角〔或直角三角形〕的探究3、平分角〔或相等角〕的探究4、平移图形后重叠局部面积函数的探究5、三角形〔或多边形〕最大面积的探究6、图形变换中特殊点活动范围的探究三、解题方法：1、画图法：〔从形到数〕一般先画出图形，充分挖掘和运用坐标系中几何图形的特性，选取适宜的相等关系列出方程，问题得解。画图分类时易掉情况，要细心。2、解析法：〔从数到形〕一般先求出点所在线〔直线或抛物线〕的函数关系式，再根据需要列出方程、不等式或函数分析求解。不会掉各种情况，但解答过程有时较繁。四、解题关键：1、从数到形：根据点的坐标特征，发现运用特殊角或线段比2、从形到数：找出特殊位置，分段分类讨论五、实例分析：〔荆州压轴题编〕如图，求△OAE右移t〔0＜t≤3〕时，△OAE与△ABE重叠局部面积函数关系式。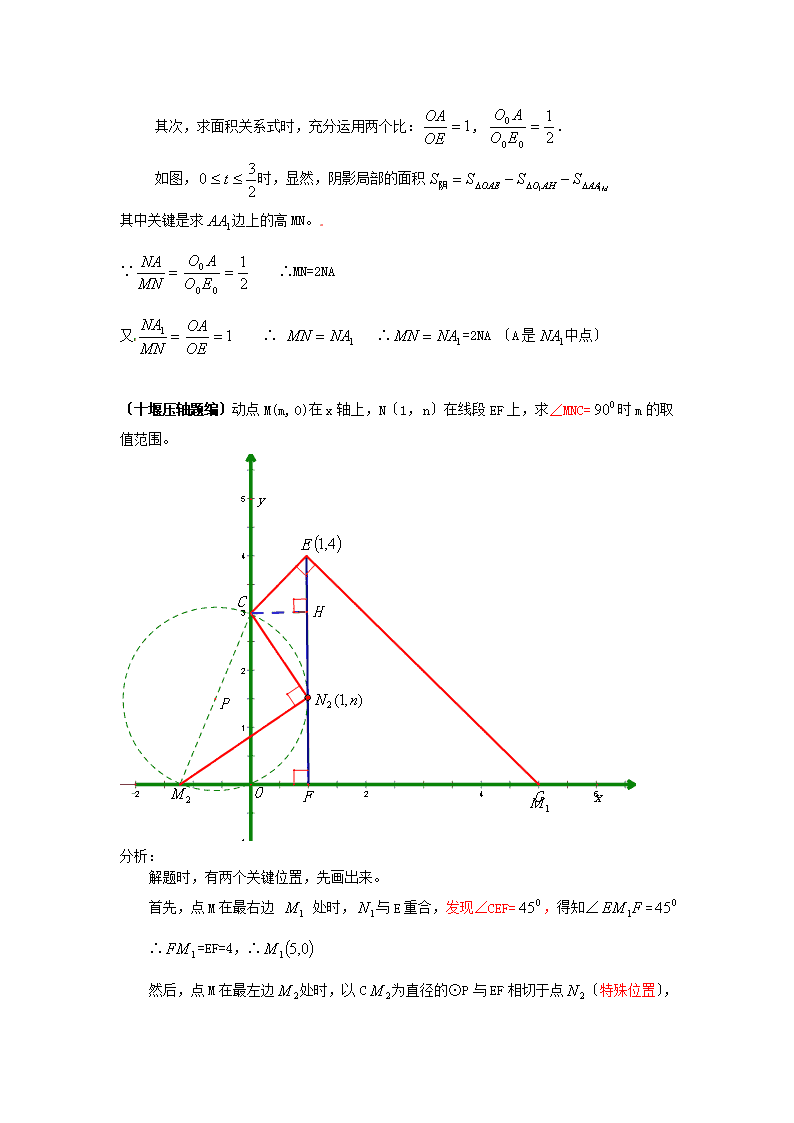分析:解题关键，首先，求右移过程中，到达零界位置〔点E落在AB上〕的时间t=，然后对时间进行分段分类讨论:，； 其次，求面积关系式时，充分运用两个比：,.如图，时，显然，阴影局部的面积其中关键是求边上的高MN。∵∴MN=2NA又∴∴=2NA〔A是中点〕〔十堰压轴题编〕动点M(m,0)在x轴上，N〔1，n〕在线段EF上，求∠MNC=时m的取值范围。分析：解题时，有两个关键位置，先画出来。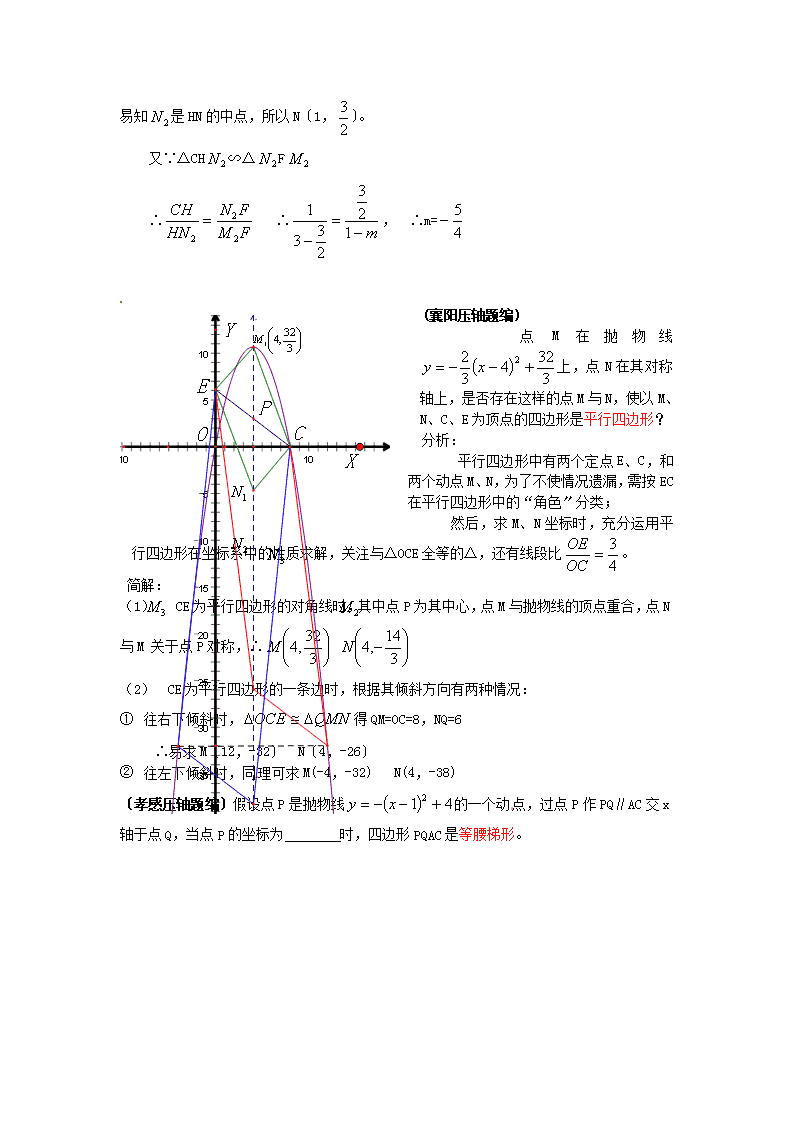首先，点M在最右边处时，与E重合，发现∠CEF=，得知∠=∴=EF=4，∴然后，点M在最左边处时，以C为直径的⊙P与EF相切于点〔特殊位置 〕，易知是HN的中点，所以N〔1，〕。又∵△CH∽△F∴∴，∴m=(襄阳压轴题编)点M在抛物线上，点N在其对称轴上，是否存在这样的点M与N，使以M、N、C、E为顶点的四边形是平行四边形？分析：平行四边形中有两个定点E、C，和两个动点M、N，为了不使情况遗漏，需按EC在平行四边形中的“角色〞分类；然后，求M、N坐标时，充分运用平行四边形在坐标系中的性质求解，关注与△OCE全等的△，还有线段比。简解：（1）CE为平行四边形的对角线时，其中点P为其中心，点M与抛物线的顶点重合，点N与M关于点P对称，∴（2）CE为平行四边形的一条边时，根据其倾斜方向有两种情况：①往右下倾斜时，得QM=OC=8，NQ=6∴易求M〔12，-32〕N〔4，-26〕②往左下倾斜时，同理可求M(-4，-32)N(4，-38)〔孝感压轴题编〕假设点P是抛物线的一个动点，过点P作PQ∥AC交x轴于点Q，当点P的坐标为时，四边形PQAC是等腰梯形。 分析：①、关注线段比得到②、运用等腰梯形的轴对称性画出图形，用解析法求解较简捷。简解：作AC的垂直平分线交x轴于点M，垂足为点N，连结CM交抛物线于点P，作PQ∥AC交x轴于点Q，四边形PQAC即为所求。由，可求出M〔4,0〕.再求出直线CM解析式与抛物线解析式联立起来求解，即使点P的坐标。〔恩施压轴题编〕假设点P是抛物线位于直线AC上方的一个动点，求△APC的面积的最大值。 分析：求坐标系中斜放的三角形面积时，简便方法是：三角形面积=水平宽×铅垂高÷2这里求三角形最大面积，用解析法简便些。先求出直线AC函数关系式，那么铅垂高PE=∴S==〔咸宁压轴题编〕如图，当MB∥OA时，如果抛物线的顶点在△ABM内部〔不包括边〕，求的取值范围。 分析：由题意知，当MB∥OA时，△ABM是等腰直角三角形；又由得其对称轴为定直线：顶点纵坐标为：按要求得：∴〔黄冈压轴题编〕在第四象限内，抛物线〔m>0〕上是否存在点F，使得点B、C、F为顶点的三角形与△BCE相似？假设存在，求m的值。分析：函数中含有参数，使问题变得复杂起来。但我们解决问题时，把它当成数看待即可。由于解析式中含有参数，故抛物线形状是可变的。所以不能画出准确的图形，只能画出示意图辅助求解。但不难得知其图像总过两定点B〔-2,0〕和E〔0,2〕，那么△BCE中有特殊角∠EBC=，由此相似分为两类。 在求解过程中，由于动点F〔，〕和参数，存在三个未知数，因此需要三个相等关系才能求解。简解：（1）△EBC∽△CBF时，设F〔，〕。由∠EBC=∠CBF=得到=--2由相似得得到由点F在抛物线上，得到联立上述三式，转化得∴〔舍去〕〔2〕△EBC∽△CFB由∠ECB=∠CBF得EC∥BF得到BF：由相似得得到由点F在抛物线上，得到联立上述三式，转化得得出矛盾0=16，故不存立。〔武汉压轴题编〕抛物线向下平移〔>0〕个,顶点为P，如图，当NP平分∠MNQ时，求的值。 分析：含参数的二次函数问题，把参数当数看待。关键是通过求点N的坐标时，发现∠NMQ=，〔很隐蔽〕另外还要发现和运用HP=HN，建立方程求解。在求解的过程中，假设用原参数表示函数关系，过程较繁，假设设新参数M〔-t,0〕,那么过程简捷一些。简解：设M〔-t,0〕，那么平移后抛物线为=和直线AB：y=2x-2联立起来得点N坐标〔2+t,2+t+t〕∴MQ=NQ∴∠NMQ=可推出HP=HN，于是得∴t=-2∴m=2