三维四向编织复合材料改进模型弹性性能计算 5页

2014年1月北京航空航天大学学报January2014第40卷第1期JournalofBeijingUniversityofAeronauticsandAstronauticsVol·40No·1三维四向编织复合材料改进模型弹性性能计算刘振国商园春董阿鹏吕明云(北京航空航天大学航空科学与工程学院，北京100191)摘要：针对三维四向编织复合材料，在改进的矩形截面单胞模型的基础上，考虑了相邻纤维束之间的界面粘结效应，推导了单胞的几何特性与编织2-_艺参数之间的数学关系，并且采用ANSYS软件建立了实体有限元模型，得到了等效弹性性能参数；之后，分析了各工艺参数对弹性模量的影响规律．通过有限元计算的材料弹性性能常数与试验数据符合较好，较为真实地模拟了该材料的细观结构，对三维编织复合材料的设计和工艺具有一定的参考价值．关键词：三维四向；编织复合材料；矩形截面单胞；界面；有限元模型中图分类号：TB332文献标识码：A文章编号：1001—5965(2014)01-00001-05Elasticpropertiescomputationforthree-·dimensionalandfour·-directionalbraidedcompositesbasedonallimprovedmodeILiuZhenguoShangYuanchunDongApengLtiMingyun(SchoolofAeronauticScienceandEngineering，BeijingUniversityofAeronauticsandAstronautics，Beijing100191，China)Abstract：Inordertostudythethree．dimensionalandfour—directionalbraidedcompositesonthebasisofanimprovedunitcellmodelwithrectangularcross—section，therelationshipbetweenthegeometricpropertiesofthecellsandthebraidingparameterswerededucedwithconsideringtheeffectsofadhesivelayersbetweenad—jacentyarns．TheANSYSsoftwarewasusedtobuildafiniteelementmodel(FEM)andobtainedequivalente·lasticperformanceparameters．Theeffectsofthemainprocessparametersontheelasticpropertiesweredis—cussed．Thecalculationresultsbythefiniteelementmodelcoincidewellwiththeexperimentaldata，whichcanrelativelytrulyreflectthemicro—structureofthismaterial．Theyhavethecertainreferencevalueforthethree—dimensionalbraidedcompositesdesignandtechnology．Keywords：three—dimensionalandfour—directional；braidedcomposites；rectangularsection；adhesivelayers；finiteelementmodel(FEM)三维编织复合材料以整体编织预成型件作为增强材料，不需缝合和加工，具有明显的可设计性，且具有较高的强度、刚度、较好的抗冲击性和耐烧蚀性等，因而受到工程界的普遍关注，特别是在航空航天等高科技技术领域得到了日益广泛的应用．有限元计算方法是进行三维编织复合材料细观分析的一种重要方式．文献[1]将纤维束和基体分别处理为梁元和杆元建立三维桁架结构有限元模型；文献[2]基于变分原理，用有限多相元法来预测三维编织复合材料的有效性能；文献[3]建立了有限元刚度预报模型；文献[4]还先后对三维编织复合材料的几何结构、物理性能和弹性模量的预测进行了论述，用非线性有限元对编织复合材料进行了数值仿真；文献[5]在等应力和等应变加权平均模型基础上建立了三维编织复合材料新的单胞几何结构模型，并提出了等效有限元方法；文献[6]提出基于大单胞的有限元分析模型，仿真了编织复合材料单胞在各种受力状态下的应力场；文献[7]通过均匀化理论，采用非协收稿日期：2013-03—27；网络出版时间：2013--06-2414：34网络出版地址：www．cnki．net／kcras／detail／l1．2625，V．20130624．1434．001．html作者简介：刘振国(1962一)，男，河北涞水人，教授，liuzg@buaa．edu．cn． 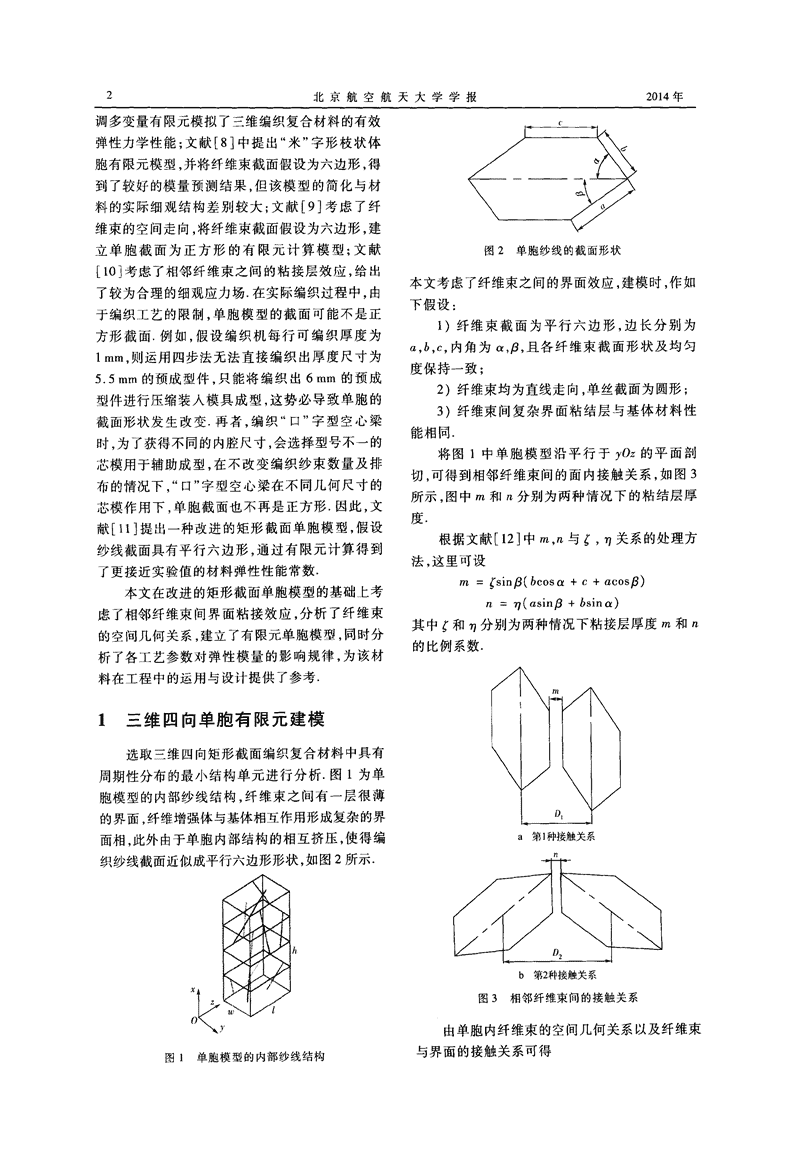2北京航空航天大学学报调多变量有限元模拟了三维编织复合材料的有效弹性力学性能；文献[8]中提出“米”字形枝状体胞有限元模型，并将纤维束截面假设为六边形，得到了较好的模量预测结果，但该模型的简化与材料的实际细观结构差别较大；文献[9]考虑了纤维束的空间走向，将纤维束截面假设为六边形，建立单胞截面为正方形的有限元计算模型；文献[10]考虑了相邻纤维束之间的粘接层效应，给出了较为合理的细观应力场．在实际编织过程中，由于编织工艺的限制，单胞模型的截面可能不是正方形截面．例如，假设编织机每行可编织厚度为1m／ll，则运用四步法无法直接编织出厚度尺寸为5．51131"11的预成型件，只能将编织出6mm的预成型件进行压缩装入模具成型，这势必导致单胞的截面形状发生改变．再者，编织“口”字型空心梁时，为了获得不同的内腔尺寸，会选择型号不一的芯模用于辅助成型，在不改变编织纱束数量及排布的情况下，“口”字型空心梁在不同几何尺寸的芯模作用下，单胞截面也不再是正方形．因此，文献[11]提出一种改进的矩形截面单胞模型，假设纱线截面具有平行六边形，通过有限元计算得到了更接近实验值的材料弹性性能常数．本文在改进的矩形截面单胞模型的基础上考虑了相邻纤维束间界面粘接效应，分析了纤维束的空间几何关系，建立了有限元单胞模型，同时分析了各工艺参数对弹性模量的影响规律，为该材料在工程中的运用与没计提供了参考．三维四向单胞有限元建模选取三维四向矩形截面编织复合材料中具有周期性分布的最小结构单元进行分析．图1为单胞模型的内部纱线结构，纤维束之问有一层很薄的界面，纤维增强体与基体相互作用形成复杂的界面相，此外由于单胞内部结构的相互挤压，使得编织纱线截面近似成平行六边形形状，如图2所示．图1单胞模型的内部纱线结构图2单胞纱线的截面形状本文考虑了纤维束之间的界面效应，建模时，作如下假设：1)纤维束截面为平行六边形，边长分别为。，b，c，内角为Ⅱ，JB，且各纤维束截面形状及均匀度保持一致；2)纤维束均为直线走向，单丝截面为圆形；3)纤维束间复杂界面粘结层与基体材料性能相同．将图1中单胞模型沿平行于yOz的平面剖切，可得到相邻纤维束间的面内接触关系，如图3所示，图中m和n分别为两种情况下的粘结层厚度．根据文献[12]中m，n与f，77关系的处理方法，这里可设m=(sin卢(bcosd+c+aCOS卢)n=叼(asin』B+bsind)其中f和"7分别为两种情况下粘接层厚度m和n的比例系数．a第】种接触关系nb第2种接触关系图3相邻纤维束间的接触关系由单胞内纤维束的空间几何关系以及纤维束与界面的接触关系可得 第1期刘振国等：三维四向编织复合材料改进模型弹性性能计算3tany：华v／lf+w2㈩Dl=(1+f)sinfl(bcosa+C+acosJB)(2)卟嘉寺㈩。z=(1+叩)(asin卢+bsina)2i了等⋯rccos万畚㈩卢⋯⋯s万志㈩asinfl—bsind=0(7)Js=2删ind+矿12sin2d+口6sin0lcosfi(8)-s=叫翁占‘1㈩其中，Ⅳ为纤维单丝数；d，为单丝直径；s为纤维束的敛集率；S为复合纤维束的横截面．y，为纤维在整个胞体中的体积分数．联立各方程式，求得建立内胞实体有限元模型所需的各个参数，采用ANSYS的APDL程序设计语言建模分析，有限元模型如图4所示．C纱线网格模型d基体网格模型图4三维四向内部单胞实体有限元模型为保证内部胞体满足周期性边界变形和应力的连续性，网格划分采用文献[10]的基本思想，各个相对面的网格划分完全相同，即对应面上的节点也是一一对应的；胞体内部纤维柱可以看作由纤维与树脂合成的单向纤维复合材料，具有横观各向同性的特点．ANSYS中SOLID95单元可以描述不规则的形状并且不损失精度，同时可以定义包括正交各向异性在内的材料特性，因此选用SOLID95单元对内部纤维柱进行体网格划分．为了便于有限元分析，将纤维束间界面粘结层看作是基体的一部分，认为其是线弹性各向同性材料，采用具备二次位移模式的SOLIDl86单元，能更精确地建立描述基体这一不规则结构的体网格．边界条件的施加采用文献[9]的思想．2有限元计算结果与讨论三维四向编织复合材料可看成是由编织纱束与树脂基体两种材料组成，其中编织纱束可看成由纤维与树脂合成的单向纤维复合材料柱体并认为是横观各向同性的．由于纱线沿空间不同取向具有不同的材料主向，因此，需沿每一种取向的纱线建立独立的局部坐标系，并分别设置材料属性．所用编织材料为碳纤维(T300，12K)，基体材料为环氧树脂，其性能参数如表1所示．表1碳纤维与树脂基体的弹性性能参数材料组分El／GPaE2／GPaG12／GPaG23／GPa肛l2p23碳纤维22013．89．04．80．200．25环氧树脂4．54．50．34同时，为了验证模型的有效性和计算结果的合理性，本文采取f=W时的正方形单胞截面与已有的实验结果¨3‘和文献[9]的有限元模型的计算结果进行对比．文献[13]中拉伸实验在MTS万能材料实验机上进行，加载速度为1mm／min，环境温度为15℃，湿度为18％．拉伸试件采用矩形板状编织件，沿编织方向的长度为160mm，横截面尺寸为20mmx6mm．由于三维编织复合材料实验件垂直于编织方向的横截面外形尺寸通常都比较小，无法沿横截面的长度或宽度方向进行拉伸实验，所以目前的拉伸实验研究主要集中在沿编织方向进行拉伸，研究此方向的弹性模量和泊松比．表2中列举了3种不同编织角p和纤维体积分数制件沿编织方向的弹性模量与泊松比的实验和计算对比数据．从对比数据可以看出，本文的分析方法和有限元计算模型是合理的．表2数值计算结果与实验结果对比此外，通过有限元分析计算得到了三维四向矩形截面编织复合材料各弹性常数随编织角、纤维体积含量及单胞截面长宽比的变化趋势曲线如图5所示．馥一盈 4北京航空航天大学学报2014年舢。1ax方向弹性模节lO8061鼍020／(。)d"-=方向剪切模鞋创f。1by方I旬弹性模罱创f。1e—t方向剪切模量45403530252015lO5O10203040506070洲f。10／(。)o／(。)g)-z方向泊松比hx。方向{『|，|松比图5等效弹性性能与编织工艺参数问的变化关系1)由图5a可知，材料纵向弹性模量E：受工艺参数编织角0的影响最大，受纤维体积含量K影响次之，受单胞截面宽与长之比A(A=w／1)影响最小．E：随着0的增大而不断减小，0<500时，E。递减迅速，此时，在0一定的情况下，y，对E。影响较为显著，A几乎不产生影响；0>50。时，E。递减趋于平缓，此时，■与A对E。的影响都不显著．2)由图5b可知，0<40。时，沿材料宽度Ⅲ方向的弹性模量E。受0，Vf和A这三者的影响都较小；0>40。时，A≠0．5时，E，随0的增大而增大．A=0．5时，E，几乎不随0的变化而变化．在H相同的情况下，0较大时，A对E，的影响明显．3)由图5c可知，0<400时，沿材料长度Z方向的弹性模量E，受工艺参数影响相对较小；0>400时，当0和H一定，E：随A的减小而增大．4)由图5d可知，材料的横向剪切模量G，：随0的增大而增大，在0<300时，G，：受U和A影响较小，而在0>300时，u越大，G，：也越大．在y，一定的情况，G，：随A的减小而呈减小趋势．5)由图5e、图5f可知，材料的纵向剪切模量酬l。1¨方向泊松比G。G。，随0的增加先增大后减小，材料在0为45。左右时，G。G，，均达到最大值．0与A一定时，两种材料的G。，G，，随坼的增加而增大，并且在峰值附近受y，的影响最大．K和0一定时，A越小，G。：越大，G。，则反之．6)由图59可知，K和A一定时，材料的横向泊松比p，：随0的增大先缓慢减小后迅速增大．当0较大时，A对弘，：产生一定的影响．7)由图5h可知，K和A一定时，材料的纵向泊松比肛；：均随0的增大先增大后减小，在0为300左右时取得最大值．"和0一定时，A越大，p。：越小，在0为30。附近时，肛；：差异最显著．8)由图5i可知，当E一定，A≠0．5时，材料的纵向泊松比肛。，随0的增大先增大后减小，在0为30。附近达到最大值．A=0．5时，肛。，随0的增大先减小后增大，并且在30。附近取得最小值．3结论1)本文基于矩形截面的单胞模型，考虑了相邻纤维柬之间的界面粘结效应，该模型与三维四向编织复合材料的内部真实结构更加接近．_)885●OOO，O======％％％％％％5I九55======}-*}一 第1期刘振国等：三维四向编织复合材料改进模型弹性性能计算2)预测了此单胞模型的三维编织复合材料的等效弹性模量，结果与已有实验结果和有限元计算结果进行了对比，较不考虑界面粘结层的有限元模型计算结果偏小，数据与实验结果吻合较好，验证了模型的有效性和计算的精度．3)讨论了编织角、纤维体积含量和截面长宽比这3个工艺参数对弹性性能的影响规律，进一步总结出，单胞截面的长宽比对材料弹性性能影响不容忽视．在进行复合材料设计时，可以根据上述工艺参数的变化，综合复合材料的各项力学性能指标，提高产品的可设计性．参考文献(References)[1]Leic，CaiYJ，KoFK．Finiteelementanalysisof3Dbraidedcomposites[J]．AdvancesinEngineeringSoftware，1992，14：187—194[2]CbenL，TanXM，ChoyCL．Mechanicalanalysisof3Dbraidedcompositesbythefinitemuhiphaseelementmethod[J]，Com—positesScienceandTechnology，1999，59(16)：2383—2391[3]庞宝君，曾涛，杜善义．三维多向编织复合材料有效弹性模量的细观计算力学分析[J]．计算力学学报，2001，18(2)：231—234PangBaojun，ZengTao，DuShanyi．Meso-scopiccompulingme-chanicsanalysisofthree-dimensionalmulti·directionalbraidedcomposites[J]．ChineseJournalofComputationalMechanics，2001，18(2)：231—234(inChinese)[4]TangZX，PostleR．Mechanicsofthree—dimensionalbraidedstructuresforcompositematerials1I：predictionoftheelasticmoduli[J]．CompositeStructures，2001，51(4)：451—457[5]KalidindiSR，FrancoE．Numericalevaluationofisostrainandweighted．．averagemodelsforelasticmoduliofthree—-dimensionalcomposites[J]．CompositesScienceandTechnology，1997，57(3)：293—305[6]ZengTan，WuLinzhi，GunLicheng．Mechanicalanalysisof3Dbraidedcomposites：afiniteelementmodel[J]．CompositeStrnc-tures，2004，64(3／4)：399—404[7]SunHuiyu，DiSbenglin，ZhangNong，eta1．MicromechanicsofbraidedcompositesviamnhivariableFEM[J]．ComputersandStructures，2003，81(20)：2021—2027[8]刘振国，陆萌，麦汉超，等．三维四向编织复合材料弹性模量数值预报[J]．北京航空航天大学学报，2000，26(2)：182—185LiuZhenguo，LuMeng，MaiHanchao，eta1．Numericalpredictionofmoduliof3-Dand4-stepbraidedcomposites[J]．JournalofBeijingUniversityofAeronauticsandAstronautics，2000，26(2)：182—185(inChinese)[9]杨振宇，卢子兴．三维四向编织复合材料弹性性能的理论预测[J]，复合材料学报，2004，21(2)：134—141YangZhenyu，LuZixing．Theoreticalpredictionoftheelasticprop—ertiesofthree--dimensionalandfour·-directionalbraidedcomposites[J]．ActaMateriaeCompositaeSinica，2004，21(2)：134—141(inChinese)[10]刘振国，李东颖。张帆，等．考虑纤维束间粘接层的三维四向编织复合材料弹性性能数值预测[J]．复合材料学报，2011，28(6)：223—229LiuZhenguo，LiDongying，ZhangFan，eta1．Numericalpredic—tionfortheelasticpropertiesof3D4-directionalbraidedcorn—positesconsideringadhesivelayers[J]．ActaMateriaeComposi．taeSinica，2011，28(6)：223—229(inChinese)[11]陈思思．三维圆型编织复合材料的力学性能研究[D]．北京：北京航空航天大学，2011ChenSisi．Researchonthemechanicalpropertiesof3一Dtubularbraidedcomposites[D]．Beijing：BeijingUniversityofAero．nauticsandAstronautics，2011(inChinese)[12]黄雨霓．三维编织复合材料力学性能研究[D]．北京：北京航空航天大学，2011HuangYuni．Researchonthemechanicalpropertiesofthreedi—mensionalbraidedcomposites[D]．Beijing：BeijingUniversityofAeronauticsandAstronautics，2011(inChinese)[13]卢子兴，冯志海，寇长河，等．编织复合材料拉伸力学性能的研究[J]．复合材料学报，1999，16(3)：129—134LuZixing，FengZhihai，KouChanghe，eta1．Studiesontensilepropertiesofbraidedstructuralcompositematerials[J]．ActaMate—riaeCompositaeSinica，1999，16(3)：129—134(inChinese)