三维编织复合材料研究进展 14页

第31卷2010年第5期5月航空学报ACTAAERoNAUTlCAETASTRONAUTlCASlNlCAV01．31NO．5Mav2010文章编号：1000一6893(2010)05—0914—14三维编织复合材料研究进展汪星明1’2，邢誉峰1(1．北京航空航天大学航空科学与LT程学院，北京100191)(2．中国人民解放军94032部队，甘肃武威733003)DevelopmentsinResearchon3DBraidedCompositesWangXingmin91”。XingYufen91(1．SchoolofAeronauticScienceandEngineering，BeijingUniversityofAeronauticsandAstronautics，Beijing100191。China)(2．No．94032Unit，People’SLiberationArmy，Wuwei733003，China)摘要：重点回顾了三维编织复合材料各发展阶段的关键性成果，从研究方法和研究方向两个角度，对该领域的重要研究成果和笔者所在课题组的最新研究成果进行了评述。在编织丁艺方面，重点介绍了编织物的细观结构和适用领域。指出了细观结构对最大纤维体积分数的影响和当前流行的建模方法，并且将周期性单胞划分方法和纱线截面形状的模拟归纳为参数化建模中的两个关键问题。对力学性能的研究成果进行了综述，在试验方面，重点介绍了编织角的变化对材料各种性能的影响；在理论方面，重点评述了几种多尺度细观力学方法和特征单元法。最后，对有待于进一步研究的问题进行了展望。关键词：复合材料；三维编织；力学性能；模型建立；均匀化方法；多尺度中图分类号：V258；TB330．1文献标识码；AAbstract：Thisarticleprovidesareviewofstudiesaboutthree-dimensional(3D)braidedcomposites，focusingonthekeyachievementsofvariousstages．Importantdevelopmentsinthefield，includingthelatestworkofourgroup，arediscussedintermsofresearchmethodandorientation．WithregardtOthebraidedprocessofcomposites，theapplicationofmeso-structuresandtheirinfluencesonthemaximumfibervolumefractionarerevealed，andthepopularmodelingmethodsarealsoreviewed．Moreover，thepartitionschemesofperiodicalcellsandthesimulationofthefibersectionpatternsareviewedasthetWOkeypointsinparameterizedmodel—ing．Intheexperimentalstudies，theeffectofbraidingangleonthemechanicalpropertiesofcompositesisem-phasized，whileintheoreticalinvestigation，themuhiscalemethodsandtheeigenelementmethodarestressed．Finally，problemsthatdeservefurtherstudiesarepresented．Keywords：compositematerials；3Dbraidedfabrics；mechanicalproperty；modelbuilding；homogenizationmethod；muhiscale航空航天领域总是希望采用重量轻、强度高的材料，而符合重量和强度要求的高性能轻质合金材料价格昂贵，已经影响到航空航天工程的进一步发展。在这种形势下，寻求低成本、高性能、能大量生产的替代材料成为必然的趋势。20世纪60年代末，美国通用电器公司为满足航天领域的需求，借鉴编织绳原理发明了万向编织机(Ominiweave)，用于编织多向增强复合材料，希望以这种廉价材料代替昂贵的高温合金。他们采用三维编织的碳一碳复合材料替代高温合金制作火箭发动机部件，使火箭发动机的重量[1]收稿日期：2009—05—07；修订日期：2009—06—29基金项目：国家自然科学基金(10772014)通讯作者：汪星明E—mail：w7526@126．corn减轻了30％～50％。这次成功的尝试显示了三维编织材料的发展前景，有力地促进了新材料的研究进程，在国际上掀起了三维编织材料的研究高潮。到20世纪70年代中期，法国欧洲动力公司也发明了类似的编织机。1982年，美国Cure—agna公司又发明了“Magnaweave”编织技术，此后三维编织技术进入了快速发展期。由于三维编织复合材料采用了三维编织技术，其纤维增强结构在空间上呈网状分布，可以定制增强体的形状，制成的材料浑然一体，不存在二次加丁造成的损伤，因此这种材料不仅具备传统复合材料所具有的高比强度、高比模量等优点，还具有高损伤容限和断裂韧性以及耐冲击、不分层、抗开裂和耐疲劳等特点。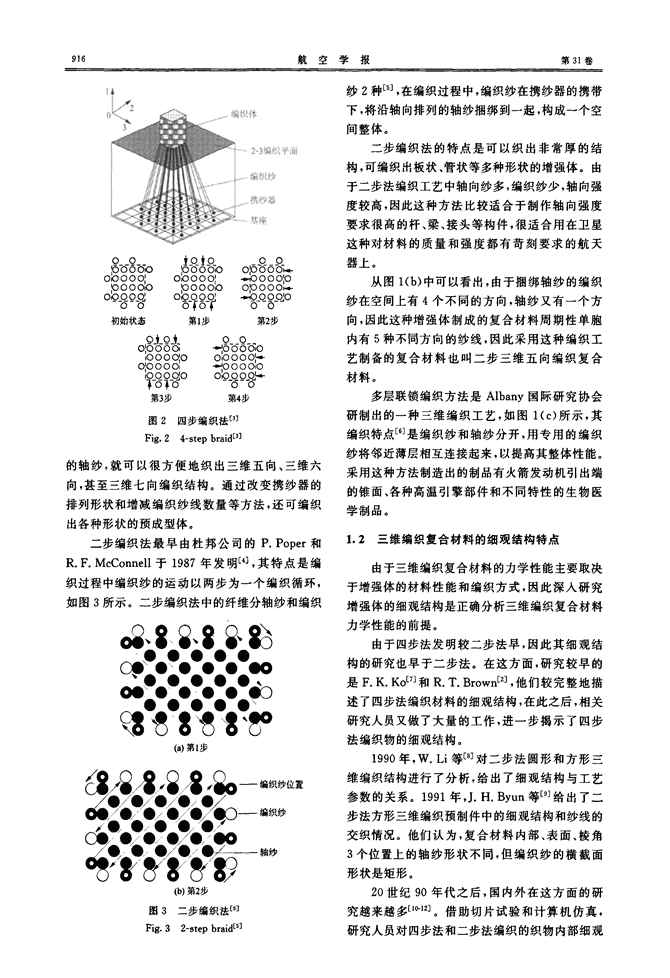这些新优点完全克服了 第5期汪星明等：i维编织复合材料研究进展传统纤维增强复合材料的缺点，又具有成本优势，因此迅速成为高性能合金的替代材料。经过数十年的发展，三维纤维增强复合材料已经在火箭、卫星、飞机等航空航天飞行器上大量应用，从火箭整流罩到喷管，从发动机支架到机身，从辅助结构到关键部件，应用量逐年提高。如今，一个飞行器上采用了多少复合材料已经成为衡量该飞行器先进程度的直观标志。最近的十几年中，三维纤维增强复合材料的应用更是普及到汽车、船舶、建筑、生物T程等各个领域，成为应用最为广泛的先进材料。三维纤维增强复合材料是采用三维纺织工艺和树脂传递模塑(ResinTransferMoulding，RTM)工艺制备的三维纺织复合材料。按纺织学定义，三维纺织复合材料可细分为三维编织、三维机织和三维针织材料3类，这三者之间的主要区别在于纺织工艺不同，所用的织机也不相同。一般来说，编织的速度慢，但是制成的织物强度高，整体性好。机织[11的速度快，但是纤维在机织过程中受到的损伤较大，材料强度会有所降低。机织物纱线交织时存在较大的曲率，承载时纱线先由弯变直，会导致结构出现较大变形，因此机织复合材料的刚度和强度都较编织材料低。针织物[13是由线圈相互穿套形成的，线圈结构使织物具有优异的延伸性和悬垂性，可以适应任何复杂形状而不产生褶皱变形，用这种材料增强的复合材料刚度较小，但具有良好的延伸性。本文重点回顾了三维编织复合材料的发展历史，对三维编织工艺、研究方法进行了归纳，总结了研究中的关键问题和主要结论，对当前研究热点和新的研究方法进行了评述，希望通过本文的工作，为相关研究人员了解三维编织的发展全貌和当前热点问题提供一个参考。1三维编织复合材料的编织方法和细观结构特点从增强体和基体的材质来看，三维编织复合材料与传统的单向或叠层纤维增强的复合材料并没有本质的不同，之所以能保留传统纤维增强材料的优点而克服了缺点，完全是由于采用了不同空间架构的增强体，因此有必要研究三维编织复合材料的编织方法和增强体内部的细观结构。1．1三维编织复合材料增强体的编织方法按编织工艺分，常见的编织材料可分为四步编织法、二步编织法和多层联锁编织法等3类，它们的预成型体的细观结构如图1所示。其中四步编织法发明最早，应用最广。按编织预制件的横截面形状，三维编织方法可分为矩形编织、圆形编织和异形编织3大类，其中矩形编织工艺适合编织矩形和板状材料的增强体，而圆形编织适合编织圆形和管型材料的增强体，异形编织则用于编织各种特殊形状的增强体。只要织物的结构形状是由矩形组合或是圆或圆的某一部分组合而成，就可以用编织方法一次成型。一黟(a)明步编织法(b)二步编织法编彩：纱轴向纱(c)多层联锁编织法图13种i维编织的纱线结构比较‘13Fig．1Comparisonoffiberarchitecturesofthreedistinctive3Dbraids[1]四步法编织工艺于1982年由R．A．Floren—tine发明【2]。这种编织工艺发明之初，所有的纱线都参加编织运动，且全部编织纱都在空间3个方向内发生相对运动，因此这种编织方法是一种真正的三维编织工艺。具体编织过程如图2所示，在一个编织周期中，编织纱沿着正交的2个方向依次进行往复运动，一个完整的编织周期中携纱器需要完成4个动作，因此被称为四步法。如图1(a)所示，由于结构中所有纱线在空间中的分布只有4个不同的方向，因此制成的复合材料被称为三维四向编织复合材料。采用这种方法制造的制品有火箭发动机的喷管、梁和管等结构。在四步法编织工艺发明后，很快就从矩形编织发展到围形编织[2]，之后又衍生出六步法和多步法，还可根据需要在长、宽、厚3个方向添加轴向不动纱，以改善预制件在该方向上的力学性能。由于编织纱有4个方向，因此通过增加不同方向 航空学报第31卷±Q±Qb000boboOo!!oOOo；oO《碑9剑OfOf第l步Q∑Qj，o!oOOo；；ooOO!oObOOo；190∞p"O}O第3步Oo",6b-o西一—HoOOo!OobOOOk--D_o_o_o：oO第2步一60西06萏oObOOOj+—一OOOo；oo：9iQ9Q卜oO第4步图2四步编织法[33Fig．24-stepbraidE3]的轴纱，就可以很方便地织出三维五向、三维六向，甚至三维七向编织结构。通过改变携纱器的排列形状和增减编织纱线数量等方法，还可编织出各种形状的预成型体。二步编织法最早由杜邦公司的P．Poper和R．F．McConnell于1987年发明r4‘，其特点是编织过程中编织纱的运动以两步为一个编织循环，如图3所示。二步编织法中的纤维分轴纱和编织(a)第l步(b)第2步图3二步编织法‘钉Fig．32-stepbraid[5]编织纱位置编织纱轴纱纱2种[5]，在编织过程中，编织纱在携纱器的携带下，将沿轴向排列的轴纱捆绑到一起，构成一个空间整体。二步编织法的特点是可以织出非常厚的结构，可编织出板状、管状等多种形状的增强体。由于二步法编织工艺中轴向纱多，编织纱少，轴向强度较高，因此这种方法比较适合于制作轴向强度要求很高的杆、梁、接头等构件，很适合用在卫星这种对材料的质量和强度都有苛刻要求的航天器上。从图1(b)中可以看出，由于捆绑轴纱的编织纱在空间上有4个不同的方向，轴纱又有一个方向，因此这种增强体制成的复合材料周期性单胞内有5种不同方向的纱线，因此采用这种编织工艺制备的复合材料也叫二步三维五向编织复合材料。多层联锁编织方法是Albany国际研究协会研制出的一种三维编织工艺，如图1(c)所示，其编织特点[6]是编织纱和轴纱分开，用专用的编织纱将邻近薄层相互连接起来，以提高其整体性能。采用这种方法制造出的制品有火箭发动机引出端的锥面、各种高温引擎部件和不同特性的生物医学制品。1．2三维编织复合材料的细观结构特点由于三维编织复合材料的力学性能主要取决于增强体的材料性能和编织方式，因此深入研究增强体的细观结构是正确分析三维编织复合材料力学性能的前提。由于四步法发明较二步法早，因此其细观结构的研究也早于二步法。在这方面，研究较早的是F．K．Ko[71和R．T．Brown[2]，他们较完整地描述了四步法编织材料的细观结构，在此之后，相关研究人员又做了大量的工作，进一步揭示了四步法编织物的细观结构。1990年，W．“等[8]对二步法圆形和方形三维编织结构进行了分析，给出了细观结构与工艺参数的关系。1991年，J．H．Byun等[9]给出了二步法方形三维编织预制件中的细观结构和纱线的交织情况。他们认为，复合材料内部、表面、棱角3个位置上的轴纱形状不同，但编织纱的横截面形状是矩形。20世纪90年代之后，国内外在这方面的研究越来越多[1¨2】。借助切片试验和计算机仿真，研究人员对四步法和二步法编织的织物内部细观|6剑-6剑。态O—o000一状I。000一。始0—p．Qp◇初 第5期汪星明等：三维编织复合材料研究进展结构已经了解得比较透彻，图1所示的纤维交织模式，就是被广泛认同的交织方式之一，但如何建立用来模拟复杂细观结构的几何模型是存在的问题。1．3编织复合材料几何模型的研究进展卢子兴m]、马文琐‘“1和邵将‘1司等在先后发表的综述中对编织材料几何模型和力学性能研究的进展进行过很好的归纳。为完整描述编织复合材料的研究进展，本文对重要部分择其要点简述，重点突出各阶段的重要成果和当前最新成果，并补充以上综述没有涉及的分支领域中比较重要的成果，尽可能为读者了解三维编织的研究全貌和查阅资料提供一个全面的参考。在20世纪90年代以前，受计算机性能的限制，研究人员不得不对复合材料的细观结构进行大幅度的等效简化，由此发展出众多的等效理论，在一定程度上解决了工程应用的迫切需要。在这一阶段，F．K．Ko等[16]提出了单胞织物几何模型(FGM)，C．L．Ma等[173给出了著名的“米”字型单胞模型。J．M．Yang等【l踟以层合板理论为基础，提出了纤维倾斜模型。在这一时期，类似的简化模型较多，其缺点是无法描述内部细观特点，其优点是计算量较小，与当时的计算能力相适应。但这些模型的模拟精度难以进一步提高，发展受到了限制。20世纪90年代以后，数值仿真能力大大加强，研究人员开始尝试对复合材料进行更高精度的等效。这一时期的研究方向高度集中于研究复合材料内部细观结构特征与基本力学性能之间的关系上，逐步建立起了符合细观结构特征的几何模型。在这一阶段，G．W．Du等[19]对单胞细观结构进行了深入的研究，并在不同的假设下给出单胞的划分方法和模型结构。在文献E203中介绍了4种不同的三维编织复合材料的编织方式，并建立了几何实体模型，给出了纤维编织角和纤维体积分数与关键编织参数之间的关系。在国内，吴德隆等[21]最早提出了可重复的基元、面元和柱元组成的三细胞模型，这种划分思想被广泛采用，三胞体模型是在此基础上逐步发展而来的。Y．Q．Wang等[22]在详细分析三维四步1×1编织过程之后，依据纤维束在编织过程中的运行方式和纤维柬之间的相互关系，提出了用控制体的方法来表征纤维柬的拓扑结构。这一阶段的工作，揭示了复合材料内部纤维交织方式，给出了基本的几何模型。随后，研究的焦点开始转移到寻找编织工艺参数与材料几何特征参数以及材料力学性能之间的关系上。目的是通过研究这两者之间的关系，寻找提高预测复合材料力学性能精度的方法和材料优化设计的方案。这方面的成果很多，J．H．Byun等[23]的工作有代表性，他们结合编织过程研究了四步法和二步法织物的细观结构，推导出关键编织参数、纤维束挤压的限制性几何条件、纤维的取向角及体积分数等相关参数之间的数学关系，为一些不具备试验手段的研究人员，研究四步法和二步法编织复合材料的性能提供了便利。韩其睿等[24]则详尽地给出了四步法有关参数之间的数学关系和推导过程，为相关研究人员提供了参考。L．Chen等[25。261结合实际编织过程，将预制件分为3个区域，对单元体几何结构进行了细分，识别了局部的单胞模型，并建立起较为合理的有限元模型，为研究人员全面了解复合材料内部细观结构给出了直观的参考。庞宝君等[273以四向编织复合材料为对象，从几何角度建立了材料单胞的组织结构模型，讨论了单胞的内部纤维束在空间上的分布规律，并进行了细观上的实验验证。徐孝诚等[2¨妇对三维编织几何胞体模型进一步进行修正，改进了单胞划分方法。以上的研究，多数是以矩形横截面材料为研究对象，随着编织材料制备技术的发展。研究人员的注意力逐渐转移到各种异形横截面材料之上。Y．Q．Wang等[10]从不同角度对管状三维编织复合材料进行了研究，他们同样采用了层合板理论，将管状编织复合材料中纱线集合体看做是曲面上交叉的层合板几何结构，又用交叉曲面层合板模型[30]对直管状编织结构从几何角度进行了描述，用半解析的方法研究了复合材料在径向物理性能上的变化规律，引用纵向有效模量和纵向泊松比的混合率计算式，用均匀化方法对直管状复合材料的弹性性能进行了数值计算并与试验结果作了对比。总之，对三维编织复合材料细观结构及其几何模型的研究，已经从简单的“米”字型大单胞逐步发展到复杂的多胞体几何模型。在常见的三维编织复合材料的细观几何结构研究方面，已经取得了较为成熟的成果，并建立了较为精细的几何模型。用有限元方法分析单胞模型来预测复合材料的宏观力学性能，也被学术界认为是一种简单 航空学报第31卷而可靠的方法，并得到了工程实践的验证。由于编织复合材料的力学性能主要取决于编织方法，而四步法和二步法编织过程的变化能力有限，为了开发出性能更加优异的编织材料，越来越多的研究人员将眼光投入到复合材料的优化设计和新编织工艺的开发之上。2001年，T．Makiko等[3叼介绍了多种矩形横截面及其组合和矩形中空横截面的编织工艺，提出了纱线阵列的优化设计公式，可用于实际编织体的生产工艺过程。马文锁等[14]采用对称群理论，将编织纱线等效为不同的点符号，推导出新的纱线交织形式，为设计新的编织工艺提供了参考。在最近10年中，专门讨论编织几何模型的文献在国内外范围内都大幅度减少。四步法、二步法编织材料的研究正在降温，而国外关于多层联锁编织的研究则方兴未艾。联锁编织物的研究方法基本相似，主要是直接建立代表性单胞(RVE)的有限元模型，计算材料的等效弹性常数，并以此为基础进行后续的研究。S．V．Lomov等[32]详细介绍了多层联锁编织物的分析方法，并总结相关研究成果，列举了截面形状分别为圆形、椭圆形、矩形和凸透镜形4种情况下的编织纱与轴向纱的截面处理方式。从这4种情况可以看出这种编织物纱线截面形状的基本处理原则：一般情况下，编织纱和轴纱都可以处理成扁平的透镜形，在较厚的联锁编织物中，编织纱可以被处理成圆形截面，而松散不互相接触挤压的编织物，所有纱线都可以处理成圆形。在多层联锁编织物的研究中，基本不采用四步法和二步法中广泛采用的“直纱线”假设，对编织纱和轴向纱在交织时的弯曲有了精细的刻画。当然，不采用“直纱线”的主要原因是多层联锁织物的结构相对简单，实现弯曲交织建模和划分网格都比较容易。X．D．Tang等[33]研究了2×2轴向编织复合材料的几何模型，分析了材料内部纤维束的挤压对纤维束形状的影响，对纤维束的“WavinessRatio”和编织角与材料力学性能方面的关系进行了研究，并通过有限元分析预测了编织角和纤维束波形形状的变化对面内性能与面外性能的影响。A．Miravete等[34]对三轴向编织材料的几何模型进行了研究，并在“米”字单胞的基础上，添加了4条平行的边界线，建立起解析模型。解析模型和有限元模型的预测结果相当接近。从检索到的文献看，类似的研究较少。在计算机性能不断提高的今天，解析模型和有限元技术相结合是理论成果走向应用的可行方法。综观这方面的研究成果，可以得出以下结论：(1)采用四步法和二步法编织的复合材料，在细观结构上都可以划分为面胞、角胞和内胞3种周期性胞体。(2)关于代表性胞体的研究趋势是由大幅度简化到精细模拟。(3)现阶段的几何模型都以代表性体积单元为基本模拟单位，通过不同的截面假设，推导出编织参数和几何参数之间的关系，用有限元法建立起符合细观交织结构的实体模型。(4)已有编织材料的内部细观结构研究都已经比较充分，难点集中在如何提高模拟精度和效率上。1．4参数化建模中的两个关键问题在建立单胞的有限元模型时，有2个必须解决的关键问题：①如何划分面胞、角胞和内胞这3种周期性单胞，不同的划分方法，得到的单胞细观结构不同；②如何模拟纱线的截面形状，不同的截面形状，影响着模型中所能达到的纱线体积分数，并直接影响模拟精度。对周期性单胞划分方法的不同意见主要存在于四步法中。为简单起见，这里只给出比较流行的两种划分方法，如图4所示。角胞圈图(a)面胞圆因角胞骶角胞圈内胞囡【”图4周期性胞体的两种不同划分方法‘“3Fig．4Schematicillustrationofinterior$ul。faceandcor—nerofapreform[26]第1种划分方法如图4(a)所示，这种方法所得到的周期性内胞取向与端面成±45。的夹角，内部胞体与边角胞体之间呈锯齿状连接。这种划分方法的优点是真实反映了纤维柬的空间走向，边 第5期汗星明等：三维编织复合材料研究进展角胞体中的纤维为曲线，能够保证模型中纤维连续不断，比较符合实际的编织结构。缺点是其模型体积分数的表达式与编织纱线的行列数的取值奇偶相关，不能用同一个表达式表达。另一种单胞的划分方法如图4(b)所示，这种方法得到的周期性内部胞体取向与端面平行或垂直，这种方法的好处是各区域单胞体积分数表达式与编织纱线的行列数取值奇偶性无关，便于材料的设计与优化。对于纱线截面形状问题，研究人员做了大量的切片试验。通过电镜观察发现，内部纱线柬的截面形状大致有圆形‘引、椭圆形[23|、菱形‘26]、凸透镜形[233等多种形状。对边角部的纱线，倾向于用三角形[26]来模拟。在有轴向纱的编织体内。轴向纱的截面则被认为接近矩形。由于编织角的存在，圆形截面的纱线束在单胞横截面上也会呈现椭圆形，而菱形和凸透镜形接近于椭圆形，因此研究者们倾向于将内部编织纱的截面形状等效为椭圆形。庞宝君等[z7]通过实际观测，认为三维四向编织材料的纱线束截面形状近似为椭圆形，如图5所示。由于实际材料中，纱线的截面形状变化较图5试件几何结构r273Fig．5Geometryofspecimen[27】大，因此究竟该用哪种几何形状来模拟纱线截面形状，暂时还没有取得共识。把纱线截面形状等效为圆形或椭圆形的研究很多，但是这些方法除了在划分网格上存在困难外，还存在难以准确模拟纤维体积分数的问题。在实际材料中，纱线截面形状会随着挤压程度的变化而变化。而打紧工序和RTM成型工艺又对纱线之间的压紧方式存在着不可控制的影响，因此纱线束的实际挤压点远比理论挤压点要多。在一束纤维的两个相邻交织点之间，纱线由于受到多处挤压，因此也不能保持着理想的直线形式和固定的截面形状。在建模时，通常会采用“直纱线”假设，即假设打紧程序会拉直纱线。由于纱线是直的，这样圆形或椭圆形截面的纱线在相切时只有一点相接触，不可能处处紧贴，也不存在弯曲，纱线间的空隙较大，因此在有限的单胞体积内，模型所能包含的纱线体积分数必定会小于材料中的实际纤维体积分数。而纤维体积分数直接和预测精度相关，当模型内的纤维体积分数低于实际值时，就会导致有限元方法预测的弹性模量等参数低于试验结果。比如文献[20]中给出的有限元预测的弹性模量值就小于试验得到的弹性模量值。根据有限元的基本原理，其预测的弹性模量应该大于试验结果。为了解决截面形状带来的体积分数上的模拟难题，田金梅等[353提出了纱线截面形状为矩形的有限元模型，用内接圆形或椭圆形的矩形截面模拟纱线束，因此该模型的体积分数与椭圆形截面相比有所提高。用矩形截面的最大优点是降低了划分网格的难度，纤维和基体之间交界面全部采用公共节点理想连接，对于宏观弹性性能的预测，矩形截面模型还是比较理想的。其不足之处是矩形截面和常见的纤维束截面存在差异。事实上，无法得到与实际情况吻合的纤维柬截面形状，任何模型都只是一种近似，这也是难以用已有模型对编织复合材料的应力特性进行比较精确分析的理由之一。多边形截面方法具有便于网格剖分和描述纤维束之间以及纤维束与机体之间的连接关系，譬如把三维四步四向复合材料的纱线束简化为包含一个含内切椭圆的八边形，将三维四步五向复合材料的编织纱线等效为含内切椭圆的六边形，不参与编织动作的轴纱则等效为矩形[361。从文献[35]和文献[36]看，多边形等效方法不仅增加了模型内部纱线束的截面积，而且相邻纱线表面可以紧密地贴合在一起，因此这种模型 航空学报第31卷的纤维体积分数会更接近实际情况。就四步法编织复合材料而言，多边形截面由于较好地兼顾了纤维体积分数、纱线截面形状和网格划分难度这3个因素，因而具有～定的优势，发展余地较大。2三维编织复合材料力学性能的试验研究进展编织复合材料力学性能的试验研究是与理论研究同时发展的。试验内容主要集中在切片、拉伸、压缩、剪切、冲击、损伤等方面。切片试验主要是为了深入了解复合材料内部细观结构，其他试验则是为了研究材料的力学性能而做的。由于复合材料具有较大的分散性且种类较多，本文不给出具体的力学性能，也不穷举所有的类似工作，只给出各个时期代表性的研究工作和被学术界共同接受的结论，为相关人员了解这方面的发展提供参考。2．1基本力学性能试验进展与传统均匀材料的力学试验不同，编织复合材料力学试验除了测试相关的力学性能数据外，还希望能够找到增强纤维的分布对材料力学性能的影响规律。在20世纪80年代，F．K．Ko[37]为了验证理论预测结果，对三维编织石墨一环氧树脂复合材料进行了拉伸试验，发现三维编织复合材料的失效是由近似垂直于加载方向失效面上的纤维断裂引起的。几乎同时，A．B．Macander等[381对树脂基多向编织纤维增强复合材料的力学性能进行了完备的力学试验。他们考虑了编织模式、纱线粗细、边界条件等各种参量对复合材料的拉抻、压缩、弯曲和层间剪切力学性能的影响。S．S．Yau等[39]对三维编织复合材料梁进行了四点弯曲和轴向压缩试验，他们在弯曲试验中发现，在初始失效之前，材料的应力应变关系呈线性形式。在20世纪90年代，编织复合材料的试验研究重点逐渐深入到材料的内部，重点考察复合材料细观结构上的细微差别对复合材料的力学性能产生的影响，同时对编织材料的理论预测结果进行验证。K．N．Shivakumar等[40]研究了三维编织复合材料内部纱线对压缩强度和失效机制的影响，发现轴向纱的错排对压缩强度的影响非常明显，而偏轴纱的错排对此影响甚微。S．R．Kalidindi等[4妇通过改变纤维体积分数和编织角，用试验的方法研究了碳一环氧树脂编织复合材料的弹性模量和强度的变化规律，并将试验结果与现有的平均应变和平均应力模型的预测结果进行了比较，证明应变应力的加权平均模型给出的结果最接近试验结果。这一时期，国内关于编织材料的试验研究也非常活跃。李嘉禄等[42]对3种不同的三维多向编织复合材料力学性能进行了试验研究，证明通过加入轴向非编织增强纤维，可以改善编织材料的拉伸强度和拉伸模量、弯曲强度和弯曲模量，并发现三维多向编织复合材料的应力应变曲线呈双线性的特征。孙慧玉等[43]对三维编织复合材料试件进行了钻孔、切割和无切割3种情况下的拉伸试验研究，通过比对受切割和未切割纤维对试件侧边拉伸应变的影响，讨论了拉伸失效的机理。试验发现，受切割和钻孔试件的拉伸性能低于未作处理试件的性能，切割侧边试件的拉伸应变高于未切割侧边的拉伸应变；并发现三维编织复合材料的孔边应力集中系数要比传统层合板复合材料和金属材料的低。卢子兴等H4]对三维四向和三维五向编织复合材料的拉伸力学性能进行了比较试验，获得了这些材料的主要力学性能参数及变形、破坏规律。对拉伸试件断口进行了电镜扫描，从细观角度对编织复合材料的破坏机制作了分析。试验证明，在相同纤维体积分数下，编织角较小时，多数纤维的破坏是拉伸破坏，材料的应力一应变关系接近线性。在编织角较大的情况下，纤维的破坏形式较为复杂，材料的应力一应变关系趋于非线性。五向编织材料沿编织方向的强度和模量一般比相同纤维体积分数的四向编织复合材料要高。但脆性也明显增加。相对于四向编织材料而言，在编织角和体积分数相同的情况下，五向编织复合材料的应力一应变关系更趋于线性化，破坏模式以脆性破坏为主。三维四向编织复合材料的压缩试验[45]证明纵向压缩模量比横向压缩模量大得多，影响纵向压缩力学性能的主要参数是材料的编织角，随编织角的变化，复合材料的纵向压缩破坏机理发生了变化，编织角较小时，材料表现为脆性特征；当编织角大于某个角度，材料的应力一应变曲线趋于非线性，延性增加，更多地表现为塑性破坏特征。横向压缩试件一般沿与受力方向成45。夹角的方向断开，这说明材料的破坏形式是剪切破坏。与纵向压缩试验不同，横向压缩试验的重复性较好， 第5期汪星明等：三维编织复合材料研究进展模量和强度的分散性均好于轴向压缩试验的情况。庞宝君等[46q7]设计了拉伸、压缩和纯剪切试验，在拉伸和压缩试验中，得到了应力一应变曲线和压缩试件的表面云纹干涉图，论述了编织角对材料破坏模式的影响，分析了循环加载、卸载的应力一应变变化规律，通过剪切试验得到了三维四向碳一环氧编织复合材料剪切弹性模量的一些试验数据，探讨了四向编织复合材料的剪切弹性模量随编织角的变化趋势。W．Lee等[48]对玻璃环氧纤维增强的三维环状编织材料板形试件进行了拉伸性能测试，测得了材料轴向和横向拉伸模量，该试验的主要目的是为了验证笔者提出的力学模型。在该模型中，笔者采用B样条曲线对三维环状编织复合材料进行了建模，用均匀化方法预测的三维环状编织材料在纵横两个方向上的弹性模量与试验结果符合得较好。类似的研究很多，基本结论则趋于一致，在不考虑材质变化的情况下，有以下结论[37-4s]：(1)三维编织复合材料的模量和强度主要受编织角和纤维体积分数的影响。(2)在编织角一定的前提下，拉伸模量随着纤维体积分数的增加而变大；拉伸断裂应变随编织角的增加而增加。(3)在纤维体积分数一定的情况下，编织角越大，编织复合材料的拉伸模量和压缩模量越小。(4)编织角越小，拉伸应力一应变曲线越接近于线性；而编织角越大，其应力一应变越表现出非线性。(5)弯曲模量和弯曲强度会随纤维体积分数及表面编织角的增加而增加，也会随着纤维体积分数及表面编织角的逐渐达到上限而趋于极限值。(6)编织复合材料的破坏模式与其结构参数的关系密切，并主要受纤维体积分数和编织角的影响。(7)三维编织复合材料内部的应变场在细观上表现为非均匀性。2．2冲击、蠕变、疲劳、损伤等工程力学性能试验研究进展进入21世纪之后，三维编织复合材料的试验开始向工程应用中急需了解的冲击、蠕变、摩擦、疲劳、损伤等工程力学性能方向转移。由于材料品种和研究方向各不相同，因此这一阶段的研究显得比较孤立，相似的研究较少，共性的结论较少，这说明三维编织复合材料的试验研究还不够充分。有待于进一步加强。沈怀荣[1鲴采用国防科学技术大学的轻气炮对三维编织结构复合材料进行了高速对称碰撞试验和弹丸穿靶试验，研究了弹丸的冲击能量与损伤区穿透直径的关系。试验证明，冲击破坏的机理是以基体材料的开裂和纤维断裂形式为主的。刘宁等哺o]利用冲击加载试验装置对含V型裂纹碳纤维编织复合材料梁的冲击损伤与断裂行为进行了试验研究，结果表明：无论是偏置裂纹或对称裂纹，复合材料裂纹尖端始终处于复合型应力场中，只是对称裂纹时II型成分较小，I型成分较大；在同样的冲击情况下，对称裂纹尖端的损伤起裂时间早于偏置裂纹的起裂，并且前者的完全损伤与断裂时间少于后者；对称裂纹扩展面基本朝向沿冲击载荷作用点，但是偏置裂纹的裂纹扩展面沿裂纹尖端面延伸，这一点与含偏置裂纹的各向同性材料梁的断裂相比具有显著的差别；编织复合材料的微观损伤与断裂机理主要涉及基体裂纹、纤维断裂、界面分层、裂纹分叉等模式。姚学锋等[s叼利用数字散斑相关方法对玻璃纤维／环氧树脂编织复合材料在三点弯曲载荷作用下裂纹损伤演化增长的力学行为进行了试验研究，通过记录裂纹尖端局域场形变散斑图像的方式，提取出不同加载水平下的位移场，得到了裂纹扩展过程中其尖端的应力强度因子与能量释放率的变化规律。试验证明，裂纹的损伤变形及其扩展是由基体损伤、纤维断裂和界面撕裂等变形模式共同作用的结果。王玉果[52]和Y．Z．Wan[53]等采用MM一200型摩擦磨损试验机研究了三维编织碳纤维／环氧(C3D／EP)复合材料在润滑条件下与淬火中碳钢轮的摩擦和磨损性能，探讨了载荷及滑动速度等外界因素的影响，通过电子显微镜观察了磨损表面，分析了润滑条件下的磨损机理。结果表明，润滑条件下复合材料的摩擦磨损性能远优于干摩擦，且磨合期较短；随着载荷的增加，复合材料的摩擦系数和比磨损率降低，但滑动速度对摩擦磨损性能的影响很小；润滑条件下的磨损机理主要是磨粒磨损。通过分析不同体积比、不同纤维结构的材料[52]在干摩擦和润滑条件下的摩擦和磨损性能，得出润滑摩擦性能与载荷、速率、纤维结构和体积相关度更小的结论。李嘉禄等[54]研究了三维编织复合材料的疲劳性能和编织结构对疲劳性能的影响。进行了应 航空学报第31卷力比为0．1、试验频率为10Hz的拉一拉疲劳性能测试。试验发现，三维编织复合材料的疲劳强度(指100万次循环加载而不破坏的最大应力，也叫疲劳极限)约为其抗拉强度的60％～80％，比普通金属材料疲劳强度的相对值要高。在疲劳次数为100万次后，未破坏试件的剩余强度均高于静载拉伸强度，其原因是材料在反复拉伸之后，试件内编织纱线的取向总是更接近于受力方向。试验还发现，编织角小的试件在疲劳试验过程中模量几乎不变，其应力一应变曲线呈现出明显的线性，随着编织角的增大，应力一应变曲线开始偏离线性，模量有逐渐升高的趋势，疲劳过程中也更容易出现各种损伤，升温现象也更明显。所有这些现象的原因都是因为材料的编织角会随着拉伸疲劳试验的延续而发生缓慢变化，纱线存在向拉伸方向集中的趋势，且这种趋势随着编织角的增大而增大，因此在出现明显的破坏之前，材料的承载能力会随着拉伸次数的增加而缓慢上升。由于纱线取向改变的趋势会随着编织角的增大而增大，因此编织角越大的材料，纱线和基体之间的摩擦做功也会越大，升温现象就越明显。O．Calme等口5]通过对碳／环氧三维编织复合材料圆柱环在侧压力下的静力破坏试验，观测到破坏是从柱体中间的外侧面开始发生的，裂纹从纤维之间的缺陷处沿厚度方向扩展，并导致出现分层破坏，外表面的纱线会被拉断。整个破坏行为是渐进的，其载荷位移曲线表现为弹塑性曲线。李典森等[56]对不同编织结构、不同编织角、不同纤维体积分数和不同应力水平下的三维编织复合材料试件进行了蠕变测试试验研究。结果表明：三维四向编织复合材料的蠕变低于五向编织复合材料；编织角小的材料抗蠕变性能较好；纤维体积分数高的材料抗蠕变性能较好。并且材料所受应力水平越高，蠕变速率越高。研究发现，幂指函数可以较好地拟合三维编织复合材料的蠕变曲线。B．Z．Sun等[57]对四步编织复合材料进行了准静态和高应变率的压缩试验，主要研究了面外压缩和面内压缩(面内沿着编织的轴向，面外垂直于编织轴向)的失效过程。研究发现，在载荷相同时，面外的压缩刚度比面内方向的压缩刚度更高。在高应变率压缩情况下，应变率相同时，面内压缩刚度比面外压缩刚度更高。试验证明，复合材料在面外方向的压缩强度高于面内方向压缩强度。在临近失效阶段，2个压缩方向上的压力对应变率几乎同样敏感。照片显示，在不同的应变率下，2个方向的破坏模式都完全不同。面外压缩的主要失效模式是剪切破坏，面内压缩的主要失效模式是纱线结构破坏。从现有的文献看，编织复合材料工程力学试验证明：(1)编织角对三维编织复合材料的工程性能有很大影响。(2)编织角小的材料，在编织方向上具有较高的承载能力，疲劳、蠕变等性能更加稳定。(3)三维编织复合材料在疲劳过程中，裂纹先在纤维或基体薄弱处出现，再扩展到结合面，损伤逐渐累积，直至破坏，并有明显的破坏先兆。(4)三维编织复合材料在定向疲劳载荷作用下，增强纤维会产生向有利于承载方向运动的趋势，表现出一种“智能适应”现象。这种现象使材料具有较高的抗疲劳性能。3三维编织复合材料力学性能的理论研究通常根据平均应力和平均应变模型可以得到材料宏观弹性参数的下限和上限，由于这种平均方法简单，因此受到学术界和工程界的普遍关注。但这类方法无法描述纤维束间以及纤维束与机体间的相互作用，而且忽略了材料的棱角、表面和内部区域上的结构差异，因此其精度受到了限制C41胁59|。目前，研究三维编织复合材料力学性能的主要方法是细观力学方法。考虑纤维几何形状和纤维与机体之间相互作用的力学分析方法都可以称为细观力学方法。细观力学解析方法的主要目的是预测材料的宏观弹性性能[591。细观有限元方法或精细有限元方法E10,60-65]也是在精细分析细观结构基础之上建立的，但在纤维和机体的界面上，法向应力和切向应变连续条件得不到精确满足。细观有限元方法不仅可以预测材料的弹性模量，还可以用于分析复合材料结构的宏观特性(如模态参数)和细观特性(如应力)等。细观力学方法本质上是一种多尺度方法。细观力学解析方法的研究对象通常是一个代表性单胞。精细有限元方法的对象可以是一个单胞(用于预测弹性参数)，也可以是整个结构。编织复合材料结构是非常复杂的，因此有限元分析方法应该是首选的可行方法。然而，细观有限元方法存在计算量问题，受到计算机能力的制约。值得指出的是，若只是为了分析低阶模态和 第5期汪星明等：三维编织复合材料研究进展频率等宏观特性，利用材料等效参数和一般有限元方法即可。为了缓解计算量和精度之间的矛盾，出现了其他细观类求解方法，如数学均匀化方法(MHM)[66{7。、各向异性多尺度均匀化方法(HMM)[韶]、多尺度有限元方法(MsFEM)[691、广义有限元方法(GFEM)C70-723和特征单元方法[73-763等。数学均匀化方法的数学基础是小参数摄动，与动力学中的多尺度方法是相似的。在等效模量的预测中，需要计算影响函数或本征位移函数的导数；在细观应力的预测中，同时需要影响函数的导数和宏观应变。而影响函数及其导数、宏观应变均需要借助有限元方法来求解单胞问题。为了保证计算精度，单胞的精细有限元网格是必要的。若机体和纤维的材料特性差别比较大，还需要二次摄动。因此，对于单胞问题，其计算量与精细有限元方法是相当的。HMM、MsFEM和GFEM具有类似之处，它们都要根据边界条件求解齐次单胞问题。在HMM方法中，需要根据均匀化边界条件求解宏观单元积分点邻域内齐次平衡方程问题，来确定单胞的二次型进而建立要求解的均匀化问题；在MsFEM方法中，要根据光滑形函数边界条件在单胞域内求解齐次平衡方程以确定多尺度单元的形函数；在GFEM中，首先要根据边界条件求解关心区域(如孔穴，裂纹或其他不连续之处等)的特殊函数(或HandbookFunctions)，再利用单位分解方法(PartitionofUnity)构造考虑特殊函数并满足协调条件的单元容许位移函数。对于编织复合材料单胞问题，这些方法的计算量与精细有限元方法是相当的。在特征单元方法中[73-74]，为了保证计算精度需要建立基本有限元网格(“基本”的含义是只要保证每个单元内不存在不连续性即可)，然后形成对应的单胞总体刚度矩阵。在此基础上，把单胞看成是一个均匀有限单元，用其形函数对已经形成的单胞总体刚度矩阵进行平均，就得到了该单胞单元的刚度矩阵。由于该单胞单元的刚度矩阵在一定程度上反映了单胞的细观几何与材料特征，故称之为特征单元。这种特征单元的好处是不需要求解单胞问题、不需要等效材料参数。在三维四向编织复合材料的宏观模量和固有振动特性模拟中，得到了较好的结果。为了改进特征单元方法，Y．F．Xing等[75]提出了单胞应变能相等和变形相似2个等效条件。应变能相等的含义是特征单胞单元的应变能要与单胞细分有限元模型的应变能相等；变形相似的含义是特征单胞单元的变形要与单胞细分有限元模型的变形相似，因此这种改进的特征单元节点可以仅包含单胞的角点，也可以包含单胞细分有限元模型的所有边界节点，后者类似于子结构方法和Multigrid方法，子结构方法也是一种多尺度方法。保留单胞边界全部节点的特征单元可以用于应力分析。为了能够构造出适合宏、细观细分的特征单元方法，邢誉峰等[76-77]构造了形函数是分段定义的特征杆和特征梁单元。关于多维特征单元的构造方法仍然在研究之中。4结束语三维编织复合材料已经广泛用于航空航天、汽车船舶、机械制造等众多领域，在可以预见的将来，其应用范围还会继续扩大。相比应用而言，三维编织复合材料的理论研究和试验研究都比较滞后。在今后一段时间，本领域还存在以下问题需要研究人员去努力解决：(1)编织工艺研究进展缓慢。当前的编织方法主要集中在四步法、二步法和联锁编织之上，机织方法和针织方法制备的材料纱线交织方式也比较单一，新的纺织工艺有待开发。(2)缺乏完善的强度准则。目前的三维编织复合材料的力学性能分析多数是弹性性能的分析研究，建立相对完善的强度准则是三维编织复合材料大量使用的理论依据。(3)目前还无法准确求解三维编织复合材料的细观力学解。在预测宏观力学性能时，仍然需要采用均匀化方法。(4)对编织复合材料的疲劳寿命研究较少。(5)在如何考虑编织复合材料内部纱线横截面的变化对材料强度等力学性能的影响上，目前还没有公认有效的解决方法。(6)能够兼顾宏观解和细观解的多尺度方法，尚需要深入研究。参考文献[1]MouritzAP。BannisterMK，FalzonPJ，eta1．Reviewofapplicationsforadvancedthree-dimensionalfibertextilecomposites[J]．CompositesPartA：AppliedScienceandManufacturing。1999，30(12)：1445—1461．1-2]BrownRT．Designandmanufacturingof3-Dbraidedpre—forms[C]／／ProceedingsdtheFifthTextileStructural 924航空学报第31卷CompositesSymposium．1991．studyonstiffnessandstrengthofthree-dimensionalbrai·[3]严实，吴林志，孙雨果，等．三维四向编织复合材料有效dedcomposites[J]．JournalofMaterialsScienceb-Engi一性能的预报[J]．复合材料学报，2007，24(1)：158—166．neering，2007，25(3)：460—467．(inChinese)YanShi，WuLinzhi，SunYuguo，eta1．Evaluationof[16]KoFK，PastoreCM．Structureandpropertiesofinte—elasticpropertiesof3D4-directionalbraidedcompositesgrated3Dfabricforstructuralcomposites[C]／／VinsonJ[J]．ActaMateriaeCompositaeSinica，2007，24(1)：158一R，TayaM．RecentAdvancesinCompositesintheUnited166．(inChinese)StatesandJapan．Philadelphia；AmericanSocietyforTest-[43PopperP，McConnellRF．Complexshapedbraidedstruc—ingMaterial，1985：428—439．tures：US4719837[P3．1988．[17]MacL，YangJM。ChouTW．Elasticstiffnessofthree-[5]李嘉禄，孙颖．二步法方型三维编织复合材料的细观结构dimensionalbraidedtextilestructuralcomposites[c]∥[J]．复合材料学报，2002，19(4)：69—75．WhitneyJM．CompositeMaterials：TestingandDesign．LiJialu，SunYing．Microstructureofthetwo-steprectan—Philadelphia；AmericanSocietyforTestingMaterial，gle3Dbraidedcomposites[J]．ActaMateriaeCompositae1986：404—421．Sinica，2002，19(4)：69—75．(inChinese)[183YangJM，MaCL，ChouTW．Fiberinclinationmodelof[6]BrooksteinDS．Interlockedfiberarchitecture：braidedthree-dimensionaltextilestructuralcomposite[J]．Journalandwoven[C]／／Proceedingsofthe35thInternationalofCompositeMaterials，1986。20(5)：472．484．SAMPESymposium．1990：746—756．[19]DuGW，ChouTW，PopperP．Analysisofthree-dimen一[7]KoFK．Braiding[M]／／DostalCA．Engineeredmaterialssionaltextilepreformsformuhidirectionalreinforcementhandbook，V01．1：Composites．ASMInternational，ofcomposites[J]．JournalofMaterialsScience，1991，261987：519—528．(I)：3438-3448．[8]LiW，HammadM。E1ShiekhA．Structuralanalysisof3一[20]DuGW，KoFK．Unitcellgeometryof3-DbraidedDbraidedpreformsforcomposites．PartII：Thetwo-stepstructures[J]．JournalofReinforcedPlasticsandCompo-preforms[J]．JournalofTextileInstitute，1990，81(4)：sites，1993，12(7)i752—768．515—537．[21]吴德隆，郝照平．五向编织结构复合材料的分析模型[J]．[9]ByunJH，WhitneyTJ，DuGW，eta1．Analyticalchar一宇航学报，1993(3)：13—16．acterizationoftwo-stepbraidedcomposites[J]．JournalofWuDelong，HaoZhaoping．5Dbraidedstructuraltom—CompositeMaterials，1991，25(12)：1599—1618．posites[J]．JournalofAstronautics，1993(3)：13·16．(in[10]WangYQ，WangASD．Onthetopologicalyarnstruc—Chinese)tureof3-Drectangularandtubularbraidedpreforms[J]．[22]WangYQ，WangASD．Microstructure／propertyrela—CompositesScienceandTechnology，1994，51(4)：575一tionshipsinthree-dimensionallybraidedfibercomposites586．[J]．CompositesScienceandTechnology。1995，53(2)：[11]PandeyR，HahnHT．Visualizationofrepresentativevol-213-222．umeelementsforthree-dimensionalfour-stepbraidedtom一[23]ByanJH，ChouTW．Processmicro-structurerelation—posites[J]．CompositesScienceandTechnology。1996，56shipsof2-stepand4-stepbraidedcomposites[J]．Compo-(2)：161—170．sitesScienceandTechnology，1996，56(3)：235-251．[12]MohajerjashiS．Moreonthefiberarchitectureof3-Dbrai一[24]韩其睿，李嘉禄，李学明．复合材料三维编织结构的单元dedcomposites[R]．AIAA-1997—1404，1997．体模型[J]．复合材料学报，1996，13(3)：76—80．[13]卢子兴。杨振宇，李仲平．三维编织复合材料力学行为研HanQirui，LiJialu，LiXueming．Unitcellgeometryof3一究进展[J]．复合材料学报，2004，21(2)：1-7．Dbraidedstructureofcomposites[J]．ActsMateriaeLuZimng。YangZhenyu，LiZhongping．DevelopmentofCompositaeSinica，1996。13(3)：76—80．(inChinese)．investigationintomechanicalbehaviourofthreedimen一[25]ChenL，TaoXM，ChoyCL．Mechanicalanalysisof3Dsionalbraidedcomposites[J]．ActaMateriaeCompositaebraidedcompositesbythefinitemuhiphaseelementme-Sinica，2004，21(2)I1—7．(inChinese)thod／1]．CompositesScienceandTechnology。1999。59[14]马文锁，赵允岭，冯伟．三维编织复合材料理论研究进展(16)：2383—2391．[J]．材料科学与工程学报，2006，24(2)：631—636．[26]ChenL，TaoXM，ChoyCL．OnthemicrostructureofMaWensuo，ZhaoYunling，FengWei．Progressinginthethree-dimensionalbraidedpreforms[J]．CompositesSci—researchon3Dbraidedcomposites[J]．JournalofMateri—enceandTechnology，1999，59(3)：391—404．alsSdence&Engineering，2006，24(2)：631—636．(in[27]庞宝君，杜善义，韩杰才．三维四向编织复合材料细观组Chinese)织及分析模型[J]．复合材料学报，1999，16(3)：135-[15]邵将，温卫东，崔海涛．三维编织复合材料刚度和强度性139．能研究进展[J]．材料科学与工程学报，2007，25(3)：PangBaojun，DuShanyi，HanJieeai．Meso-structureand460—467．modelingofthee-dimensionalmulti-directionalcompositesShaoJiang，WenWeidong，CuiHaitao．Advancesof[J]．ActaMateriaeCompositaeSiniea，1999，16(3)：135- 第5期汪星明等：专维编织复合材料研究进展925139．(inChinese)[28]徐孝诚，孙德海，黄小平．三维编织复合材料细观结构的几何学分析[J]．强度与环境，1999(2)：37—43．XuXiaocheng，SunDehai，HuangXiaoping．Geometryanalysisonmicrostructureof3-Dbraidedcomposite[J]．Structure&EnvironmentEngineering，1999(2)：37—43．(inChinese)[29]黄小平，孙良新，徐孝诚．复合材料三维四向矩形编织物角柱结构研究[J]．复合材料学报，2001，18(4)：11—15．HuangXiaoping，SunLiangxin，XuXiaocheng．Cornermicrostructureof3-Drectangularbraidedpreformsforcomposites[J]．ActaMateriaeCompositaeSinica，2001，18(4)：ll一15．(inChinese)[303WangYQ，WangASD．Spatialdistributionofyarnsandmechanicalpropertiesin3Dbraidedtubularcomposites[J]．AppliedCompositeMaterials，1997，4(2)：121—132．[31]MakikoT，TadashiU，AsamiN，eta1．Structureandma—chinebraidingprocedureofcoupledsquarebraidswithva—riouscrosssectionsEJ]．CompositesPartA：AppliedSci-enceandManufacturing，2001，32(10)：1485—1489．[32]LomovSV，IvanovDS，VerpoestI，eta1．Meso-FEmodelingoftextilecomposites：roadmap，dataflowandalgorithms[J]．CompositesScienceandTechnology，2007，67(9)：1870—1891．[33]TangXD，WhitcombJD，GoyalD．Effectofbraidangleandwavinessratioofeffectivemoduliof2X2biaxialbrai—dedcomposites[R]．AIAA一2003—1877，2003．[34]MiraveteA，BielsaJM。ChiminelliA，eta1．3Dmesome—chanicalanalysisofthree-axialbraidedcompositematerials[J]．CompositesScienceandTechnology，2006，66(15)l2954-2964．[35]田金梅，邢誉峰．一种新的三维四步编织复合材料几何模型及其在宏观弹性性能预测中的应用[J]．航空学报，2007，28(1)：130-134．TianJinmei。XingYufeng．Unitcelleigen—elementof3一DorthogonalwovencompositesanditsapplicationaEJ]．ActaAeronauticaetAstronauticaSinica，2007，28(I)：130-134．(inChinese)[36]李金超．张一帆，孙菲，等．三维五向编织复合材料的力学性能分析I：细观结构模型[J]．复合材料学报，2009，26(1)：150-155．LiJinchao，ZhangYifan，SunFei，etaLMechanicsanaly—sisofthree-dimensionalfive-directionalbraidedcompositesI：microstructuralmodel[J]．ActaMateriaeCompositaeSinica，2009，26(1)：150—155．(inChinese)[37]KoFK．Tensilestrengthandmodulusofathree-dimen·sionalbraidcomposite[C]／／WhitneyJM．Compositema—terials：testinganddesign．Philadelphia：AmericanSocie—tyforTestingMaterial，1986：392—403．[38]MacanderAB，CraneRM，CamponeschiET，eta1．Fabricationandmechanicalpropertiesofmulti-。dimension‘。ally(X—D)braidedcompositematerials[C]／／WhitneyJM．CompositeNaterials：TestingandDesign(7thConf．)．Philadelphia：AmericanSocietyforTestingMate—rial，1986：422—443．[393YauSS，ChouTW，KoFK．Flexuralandaxialcorn—pressivefailuresofthree-dimensionallybraidedcompositeI--beams[J]．Composites。1986，17(3)：227—232．[40]ShivakumarKN。EmehelTC，AwaVS，eta1．COm—pressionstrengthandfailuremechanismsof3Dtextilecomposites[R]．AIAA-1995—1159，1995．[41]KalidindiSR，AbusafiehA．Longitudinalandtransversemoduliandstrengthsoflowangle3-Dbraidedcomposites[J]．JournalofCompositeMaterials，1996，30(8)；885—905．[42]李嘉椽，肖丽华，董孚允．立体多向编织结构对复合材料性能的影响[J]．复合材料学报，1996，13(3)：71—75．LiJialu。XiaoLihua，DongFuyun．Influenceofthreedi—mensionalandmultidirectionalbraidstructuresonthepropertiesofcomposites[J]．ActaMateriaeCompositaeSinica，1996，13(3)：71-75．(inChinese)[43]孙慧玉，吴长春．纺织结构复合材料力学性能的实验研究口]．实验力学，1997，12(3)：335—341．SunHuiyu，WuChangchun．Experimentalresearchonme-chanicalpropertiesofcompositematerialswithtextilestructure[J]．JournalofExperimentalMechanics，1997，12(3)：335-341．[443卢子兴，冯志海．寇长河，等。编织复合材料拉伸力学性能的研究[J]．复合材料学报，1999，16(3)：129—134．LuZixing，FengZhihai，KouChanghe，eta1．Studiesontensilepropertiesofbraidedstructuralcompositematerials[J]．AetaMateriaeCompositaeSinica，1999，16(3)：129—134．(inChinese)[45]卢子兴，胡奇．三维编织复合材料压缩力学性能的实验研究口]．复合材料学报，2003，20(6)：67—72．LuZixing，HuQi．Experimentalinvestigationintothecompressivemechanicalpropertiesofthreedimensionalbraidedcomposites[J]．ActaMateriaeCompositaeSinica，2003，20(6)：67-72．(inChinese)[46]庞宝君，杜善义，严勇，等．三维四向碳一环氧编织复合材料剪切力学性能实验研究[J]．实验力学，1999，14(2)：209—215．PangBaojun，DuShanyi，YanYong，eta1．Anexperi—mentalinvestigationfortheshearingmechanicalpropertiesofthree-dimensionfour-directionbraidedcarbon／epoxycomposite[J]．JournalofExperimentalMechanics，1999，14(2)：209-215．(inChinese)[473庞宝君。杜善义，韩杰才，等．三维四向编织碳一环氧复合材料实验研究[J]．复合材料学报，1999，16(4)：136—141．PangBaoiun，DuShanyi，HanJiecai。eta1．Experimentalinvestigationofthree-dimensionalfour-directionalbraidedcarbon／epoxycomposites[J]．ActaMateriaeCompositaeSinica，1999，16(4)：136—141．(inChinese)[48]LeeW，KimJH，ShinHJ，eta1．Constitutiveequationsbasedoncellmodelingmethodfor3Dcircularbraided 926航空学报第31卷glassfiberreinforcedcomposites[J]．FibersandPoly—metricmodel：modificationandapplicationofafabricge—mers．2003，4(2)：77—83．ometrymodeltopredicttheelasticpropertiesoftextile[49]沈怀荣．三维编织复合材料冲击实验与分析[J]．装备指composites[J]．JournalofCompositeTechnologyandRe一挥技术学院学报，2002，13(2)：84—86．search，1994，16(1)：32—36．ShenHuairong．Impactexperimentandanalysisofthree[603ChenZ。ZhuD，LuM．eta1．Ahomogenizationschemebraidedcompositematerials[J]．JournalofInstituteofanditsapplicationtoevaluationofelasticpropertiesofCommandandTechnologyofEquipment，2002，13(2)：three-dimensionalbraidedcomposites[J]．CompositesPart84—86．(inChinese)B：Engineering，2001。32(1)：67—86．[503刘宁，姚学锋．陈俊达。等．编织复合材料的冲击损伤与[61]SunHY，DiSL，ZhangN，eta1．Micromechanicsof断裂行为研究[J]．实验力学，2002，17(2)：184—189．braidedcompositesviamultivariahleFE[J]．ComputersLiuNing。YaoXuefeng。ChenJunda，eta1．ResearchoffandStructures，2003，81(20)：2021+2027．theimpactdamageandfracturebehaviorofbraidedcom一[62]LiW，HammadM，EIShiekhA．Structuralanalysisof3一posites[J]．JournalofExperimentalMechanics，2002，17Dbraidedperformsforcomposites，PartI．-thefour-step(2)：184—189．(inChinese)preforms[J]．JournalofTextileInstitute，1990，81(4)I[51]姚学锋，林碧森，张志勇，等．编织复合材料的裂纹损伤491—514．与增长行为研究口]．工程力学，2002，19(5)：118—122．[63]WuDL．Three-cellmodeland5Dbraidedstructuralcorn—YaoXuefeng。LinBisen。ZhangZhiyong，eta1．Crackposites[J]．CompositesScienceandTechnology，1996，56damageandgrowthbehaviorofbraidedcomposite[J]．En一(3)：225—233．gineeringMechanics，2002，19(5)：118—122．(inChinese)[64]MohajerjasbiS．Fiberarchitectureofthree-dimensional[52]王玉果，王玉林，吴广顺．三维编织复合材料在润滑条件braidedcomposites[J]．AIAAJournal，1998，36(4)：下的摩擦性能[J]．材料科学与工艺，2005，13(4)；365—613—617．367．[65]LiuzG，ZhangHG，LuZX，eta1．InvestigationontheWangYuguo，WangYulin，WuGuangshun．Frictionandthermalconductivityof3-dimensionaland4-directionalwearcharacteristicsof3-Dbraidedcarboncompositesan—braidedcomposites[J]．ChineseJournalofAeronautics，derlubricatedcondition[J]．MaterialsScience&Technol一2007，20(4)：327—331．ogy，2005，13(4)：365—367．(inChinese)E66]BenssousanA，LionsJ，PapanicolaouG．Asymptotic[53]WanYz，LuoHL，WangYL。eta1．Frictionandwearanalysisforperiodicstructures[M]．North-Holland：Am—behaviorofthree-dimensionalbraidedcarbonfiber／epoxysterdam，1978．compositesunderlubricatedslidingconditions[J]．Journal[67]YuxG，CuiJz．ThepredictiononmechanicalpropertiesofMaterialsScience，2005，40(17)：4475—4481．of4-stepbraidedcompositesviatwo—scalemethod[J]．[54]李嘉椽，杨红娜，寇长河．三维编织复合材料的疲劳性能CompositesScienceandTechnology，2007·67(3—4)：471一[J]．复合材料学报。2005，22(4)：172—176．480．LiJialu，YangHongna，KouChanghe．Fatigueproperties[68]WdnanE，EngquistB．Theheterogeneousmuhiscaleofthreedimensionalbraidingcomposites[J]．AetaMateri-methods[J]．CommunicationsinMathmaticalSciences，aeCompositaeSinica，2005，22(4)：172—176．(inChi一2003，1(1){87’132．nese)[69]HouT，WuX．Amuhisealefiniteelementmethodfore卜[55]CalmeO，BigaudD，HamelinP．3Dbraidedcompositelipticproblemsincompositematerialsandporousmediaringsunderlateralcompression[J]．CompositesScience[J]．JournalofComputationalPhysices,1997，134：169一andTechnology，2005，65(1)：95—106．189．[56]李典森，李嘉禄，陈利，等．三维编织复合材料蠕变行为[70]StrouboulisT，CoppsK，Babu§kaI．Thegeneralizedfi一的试验研究[J]．航空材料学报，2006，26(1)：76—79．niteelementmethodlanexampleofitsimplementationLiDiansen，LiJialutChenLi，eta1．Studiesoncreepbe—andillustrationofitsperformance[J]．InternationalJour—haviorofthreedimensionalbraidingcomposite[J]．JournalhalforNumericalMethodsinEngineering，2000，47(8)：ofA。eronauticalMaterial，2006，26(1)：76—79．(inChi-1401-1417．nese)[71]StrouboulisT，ZhangL，Babugka1．p-versionofthegen一[57]SunBz，GuBH．Highstrainratebehaviorof4-step3DeralizedFEMusingmesh-basedhandbookswithapplica—braidedcompositesundercompressivefailure[J]．Journaltionstomultiscaleproblems[J]．InternationalJournalforofMaterialsScience，2007，42(7)：2463-2470．NumericalMethodsinEngineering,2004’60(10)：1639一[58]NormanT，AllisonP，BaldwinJW，eta1．Effectoftow167Z．alignmentonthemechanicalperformanceof3Dwoven[72]BabugkaI，NistorV，TarfuleaN．Generalizedfiniteele—textilecomposites[J]．CompositesManufacturing，1993，mentmethodforsecond-orderellipticoperatorswith4(4)：209—215．Dirichletboundaryeonditions[J]．JournalofComputation一[59]PastoreCM，GowayedY九Aself-consistentfabricgeo—alandAppliedMathematics。2008，218(I)：175—183． 第5期汪星明等：三维编织复合材料研究进展927[73]XingYF，TianJM．Thehomogenizationmethodbased011eigenvectorexpansionsforwovenfabriccomposites[J]．InternationalJournalforMulti、-scaleComputationalEngi—-neering，2006，4(1)：197—206．[74]邢誉峰，田金梅．三维正交机织复合材料的单胞特征单元及其应用[J]．航空学报，2007，28(4)：881—885．XingYufeng，TianJinmei．Unitcelleigen～elementof3-Dorthogonalwovencompositesanditsapplications[J]．ActaAeronauticaetAstronauticaSinica，2007，28(4)：881—885．(inChinese)[753XingYF，WangXM．AneigenelementmethodandtwOhomogenizationconditions[J]．ActaMechanicaSinica，2008，25(3)：1614-3116．[76]邢誉峰，杨阳．形函效分段定义的夸矩粱特征单元[J]．力学学报，2008，40(2)：1—7．XingYufang，YangYang．Abendingmomentbeamdgen—elementwithpiecewiseshapefunctions[J]．ChineseJour—halofTheoreticalandAppliedMechanics，2008，40(2)：卜7．(inChinese)[77]XingYF，YangY．Anewrodeigenelementanditsappli—cationtOstructuralstaticanddynamicanalysis[C]∥Com—putationalMechanicsProceedingsof。InternationalSym—posiumonComputationalMechanics”．Heidelberg：Springer，2007．作者简介：汪星明(1975一J男，博士，工程师。主要研究方向：复合材料结构力学。Tel：13681454831E-mail：w7526@126．corn邢誉蜂(1964一)男，博士，教授，博士生导师。主要研究方向：结构动力学、复合材料结构力学。Tel：010—82319964E+mail：xiIlgyf@buaa．edu．cn(编辑：徐晓)延钢睦纷辞出裆稍稍希出希吐镭趟铂砖蝌袒希出零出裆裆稍幂出稍帛楚铂鹇秽稍希出乖出耆鸱枣毡稍窑砖希《；a池希穹5睿蛙钎％延j芥{!；带延镅；延‘筇：{}书≈窖誉《j幂《；带趟锔姑裆科目潞带。幺帝，’’’’’’、：通知：．t‘。ll‘。，“创新杯"第四届全国未来飞行器设计大赛通知为普及航空知识，激发广大航空从业者和航空爱好者的想象力和创造灵感，畅想航空未来发展蓝图，中国航空学会继成功举办三届全国未来飞行器设计大赛后，于2010年与空军装备部、中国航空工业集团公司联合举办第四届大赛，大赛由中航工业成都飞机设计研究所赞助支持。一、大赛组织机构：主办单位：中国航空学会联合主办单位：空军装备部中国航空工业集团公司赞助协办单位：中航工业成都飞机设计研究所协办单位：北京航空航天大学，西北工业大学、南京航空航天大学、中国民航大学、南昌航空大学、沈阳航空工业学院、中航工业团委、各省(市、区)航空学会二、大赛主题：蓝色天空放飞梦想——临近空问飞行器设计——未来个人飞行器设计本次大赛侧重未来飞行器的概念设计。设计重点在于构想未来人类对临近空间或个人飞行的需求，根据需求分析完成临近空间飞行器或未来个人飞行器的总体概念性设计，最后以设计图和文字报告来表现。为了加深公众对临近空间飞行器的了解，大赛特别附加了部分背景资料。参赛方式及要求、作品要求、评分标准、奖励办法、进程安排以及分赛区划分及联系方式详见学会网站www．csaa．org．cn。创新杯”第三届全国未来飞行器设计大赛办公室：咨询热线：(010)84924395；84928795传真：(010)84923942联系人：张晶姜绪金通讯地址：北京市761信箱2分箱(中国航空学会)邮编：100012E—mail；csaakpb@126．corn网址：www．csaa．org．cn；Www．hangkongnet．corn如对以上发布的内容有疑问，请致电大赛办公室，以大赛办公室解释为准。特别申明：参赛作品著作权属于作者。主办方拥有版权，有权对作品进行编辑、出版和宣传。凡报送作品参赛本次活动的，即视为已确认并自愿遵守本次活动有关版权和创作要求的各项规定。【中国航空学会)