编织几何结构的群论分析[1] 5页

第50卷第20期2005年10月论文编织几何结构的群论分析①①②*冯伟马文锁(①上海大学上海市应用数学和力学研究所,上海200072;②焦作大学机电系,焦作454002.*联系人,E-mail:mawensuo@jzu.cn)摘要将材料编织体中连续的纱线离散并用特殊的点符号表达,用点群和空间群分析现有编织材料几何结构.一方面可以合理有效地对现有编织材料几何结构进行描述和分类,另一方面也可将该理论用于导出编织材料几何结构新的和更为有效的编织方法,为优化材料性能提供理论依据.关键词编织几何结构点符号平面群空间群对称群分析在纺织材料的研究领域,几何结构的研究是其达,这种特殊的点定义为点符号.性能研究的重要基础.不同的应用领域有不同的研处于编织平面的纱线段用点符号表示.将处+究目的.现有的纺织几何结构的性能差异为科技人于编织平面上方的平行纱线段用表示,而处于编−员所共知.二维纺织几何结构品种繁多,研究历史悠织面下方的纱线段用表示.穿越编织平面的纱线[1~3]久.由于目前的三维纺织几何结构多数由经验归段用表示,指向编织平面的法线的正向一侧.简化[4,5]纳所得,因而材料品种少,研究范围受到限制.几表示时,点符号放置在纱线的轴线投影上.何结构及综合性能的研究在复合材料出现后显得尤点符号组合时必须满足纱线连续的原则,其集为重要.正确合理的几何结构模型有利于材料的力合所反映的图案经过平面群的对称操作,最终组合学分析.纵观纺织几何结构的研究历史,三维整体编图案为一合理平面编织几何结构.建立点符号的组[4~8][9,10]织的研究局限于四步法、二步法编织等少数合原则是群分析过程的重要组成部分.作为生成编几种类型.尽管确信还有结构更多、性能更好的编织织几何结构的最基本单元——基本对称单元的构建,[7]几何结构,但缺乏系统的理论支持.新的编织方法可以通过编制程序,最终实现可视化目标.的研究多数仍是在偶然性的基础上展开的.1.2基本对称单元在长期的复合材料的研究过程中,作者发现编将平面编织几何结构的图案中通过平移、滑移和织几何结构与晶体几何结构有极为相似的对称性.螺旋旋转等对称操作而覆盖整体编织平面的图案作本文用几何结构对称群将编织体中连续的纱线离散,为一个单元,称为基本对称单元.在平面二维编织几并用特殊的点符号表达,将点群和空间群用于分析何结构中,由于编织工艺的限制,纱线在编织平面内现有编织几何结构.进而把所有可能的编织材料几的投影为直线,使得构成的编织图案具有规则几何何结构进行分类,用于导出编织材料几何结构新的的特征,只可能有几种图案(如图1所示),而不会有和更为有效的编织方法,为优化材料性能打下基础.其他不规则拓扑几何图案单元.基本对称单元可以二维周期性编织几何结构图案可以用平面群加是代表一根纱线段的一个点符号,也可以是由离散以描述,三维编织几何结构也可以找到其相应的空纱线段点符号集合代表的平面图案.间群.为描述方便,这里将对应于编织几何结构的对1.3编织平面点阵称群定义为编织对称群.对应于平面二维编织几何结构的对称群称作编织平面群,对应空间三维编织将周期性二维编织图案中基本对称单元用一个几何结构的称为编织空间群.点表达,所有周期性图案就可以用规则的平面点的阵列简化,称为二维编织几何结构平面点阵.与晶体对1对应于二维编织几何结构的平面群称群的平面点阵相同,二维编织几何结构也对应5个1.1点符号平面点阵,即斜交点阵(2)、简单矩形点阵(2mm)、c编织体中连续的纱线经过离散成为不同空间位心矩形点阵(2mm)、正方点阵(4mm)和六角点阵(6mm),置的纱线段,在编织体中每种纱线段用特殊的点表见图1所示.括号内表示对应的点阵点群.2300www.scichina.com 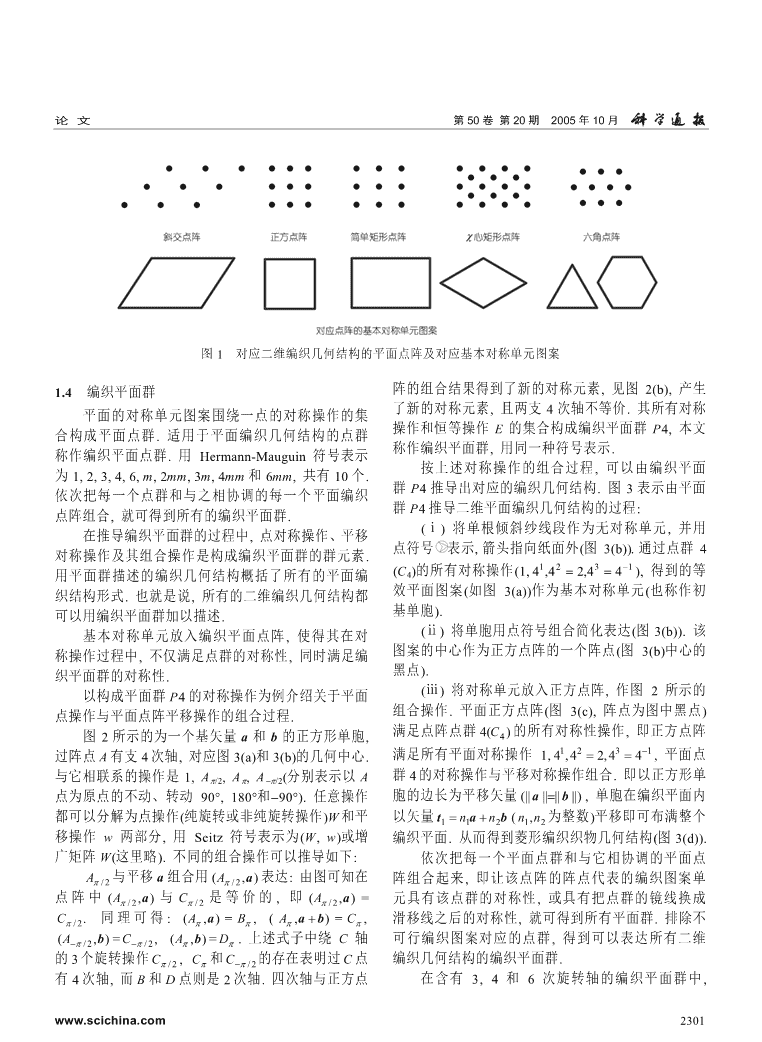论文第50卷第20期2005年10月图1对应二维编织几何结构的平面点阵及对应基本对称单元图案1.4编织平面群阵的组合结果得到了新的对称元素,见图2(b),产生了新的对称元素,且两支4次轴不等价.其所有对称平面的对称单元图案围绕一点的对称操作的集操作和恒等操作E的集合构成编织平面群P4,本文合构成平面点群.适用于平面编织几何结构的点群称作编织平面群,用同一种符号表示.称作编织平面点群.用Hermann-Mauguin符号表示按上述对称操作的组合过程,可以由编织平面为1,2,3,4,6,m,2mm,3m,4mm和6mm,共有10个.群P4推导出对应的编织几何结构.图3表示由平面依次把每一个点群和与之相协调的每一个平面编织群P4推导二维平面编织几何结构的过程:点阵组合,就可得到所有的编织平面群.(ⅰ)将单根倾斜纱线段作为无对称单元,并用在推导编织平面群的过程中,点对称操作、平移点符号表示,箭头指向纸面外(图3(b)).通过点群4对称操作及其组合操作是构成编织平面群的群元素.123−1用平面群描述的编织几何结构概括了所有的平面编(C4)的所有对称操作(1,4,4=2,4=4),得到的等效平面图案(如图3(a))作为基本对称单元(也称作初织结构形式.也就是说,所有的二维编织几何结构都基单胞).可以用编织平面群加以描述.(ⅱ)将单胞用点符号组合简化表达(图3(b)).该基本对称单元放入编织平面点阵,使得其在对图案的中心作为正方点阵的一个阵点(图3(b)中心的称操作过程中,不仅满足点群的对称性,同时满足编黑点).织平面群的对称性.(ⅲ)将对称单元放入正方点阵,作图2所示的以构成平面群P4的对称操作为例介绍关于平面组合操作.平面正方点阵(图3(c),阵点为图中黑点)点操作与平面点阵平移操作的组合过程.图2所示的为一个基矢量a和b的正方形单胞,满足点阵点群4(C4)的所有对称性操作,即正方点阵123−1过阵点A有支4次轴,对应图3(a)和3(b)的几何中心.满足所有平面对称操作1,4,4=2,4=4,平面点与它相联系的操作是1,Aπ/2,Aπ,A−π/2(分别表示以A群4的对称操作与平移对称操作组合.即以正方形单点为原点的不动、转动90°,180°和−90°).任意操作胞的边长为平移矢量(||a||=||b||),单胞在编织平面内都可以分解为点操作(纯旋转或非纯旋转操作)W和平以矢量ta11=n+n2b(n1,n2为整数)平移即可布满整个移操作w两部分,用Seitz符号表示为(W,w)或增编织平面.从而得到菱形编织织物几何结构(图3(d)).广矩阵W(这里略).不同的组合操作可以推导如下:依次把每一个平面点群和与它相协调的平面点Aπ/2与平移a组合用(Aπ/2,a)表达:由图可知在阵组合起来,即让该点阵的阵点代表的编织图案单点阵中(Aπ/2,a)与Cπ/2是等价的,即(Aπ/2,a)=元具有该点群的对称性,或具有把点群的镜线换成Cπ/2.同理可得:(,Aπa)=Bπ,(Aπ,)a+b=Cπ,滑移线之后的对称性,就可得到所有平面群.排除不(,A−π/2b)=C−π/2,(,Aπb)=Dπ.上述式子中绕C轴可行编织图案对应的点群,得到可以表达所有二维的3个旋转操作Cπ/2,Cπ和C−π/2的存在表明过C点编织几何结构的编织平面群.有4次轴,而B和D点则是2次轴.四次轴与正方点在含有3,4和6次旋转轴的编织平面群中,www.scichina.com2301 第50卷第20期2005年10月论文[11]图24次轴与正方点阵平移对称操作的组合(a)对称操作组合推导,(b)点阵的对称元素图3平面群推导二维编织几何结构(a)对应点群4正方形单胞,(b)纱线段点符号组合,(c)平面点群与平面点阵组合,(d)平面编织织物Pm4m,P4gm,Pm31,P31m和P6mm中存在单纯镜出对应空间点群与平移群的组合结果,得到描述空面反射对称元素,有图4所示不可实现的畸形图案,间编织几何结构的空间群.因而不对应实际的二维编织几何结构.有效的平面用编织空间群可以概括可能的空间编织几何结群共有12种.构.针对三维编织复合材料几何结构,绝大多数可以认为是周期性的,而对不对称编织特殊情况可以用对称性低的空间群将其编织几何结构涵盖.另外这里并不强调空间群与编织几何结构一一对应,而是一多对应关系.即一种空间群可以对应几种类似的空间几何结构,关键在于如何选择无对称单元和基图4平面群推导二维编织几何结构过程中存在畸形图案本对称单元.这种单元可以是小到单根纱线段,大到较大数量的纱线段的组合,只是必需严格满足点符２对应于三维编织几何结构的编织空间群号组合原则及空间群满足的对称性要求.为了直观地把三维编织几何结构与空间点群相不考虑纱线段在空间中方向不同的影响,描述对应,将在三维空间处于同一根纱线或相互平行的三维编织几何结构理论上也应该对应230种空间群.纱线段用同一种点符号表达(在编制程序时表示为三但在用空间群推导三维编织几何结构的过程中,由维空间坐标的矢量).在图形表达时,不同方向的纱于纱线交织几何结构的一些特殊性,使得对应编织线段可用不同颜色的纱线段区分,本文用三维空间几何结构的空间群不会达到230种.图形描述.以惯用单胞的角点或几何中心作为点阵这种特殊性体现在用空间群构造三维编织体时,的阵点,就可与三维Braivais点阵建立对应关系,找参与编织的纱线轴线必须为一条直线(实际编织体中2302www.scichina.com 论文第50卷第20期2005年10月纱线可能是周期性波浪状,但推导过程不受此影响),xy平面第二象限过坐标原点角平分线为n次轴的一决定了纱线段不能够任意放置,对称操作的结果不个对称操作,上标“−1”表示顺时针方向旋转.能构成类似图4所示的畸形图案.由编织空间群形成的三维空间任意两根纱线轴线不应相交一点,但可重合或平行.第二,用空间群推导三维编织几何结构不能违背最终纱线连续的原则.[12]在晶体学中,共有32种空间点群.32种空间点群按是否含有纯镜面反射群元素分为两类.不含有该群元素的为一类,含有m的为一类.前一种类型的空间点群有:C1(1),C2(2),C3(3),C4(4),C6(6),S2(1),S4(4),S6(3),D2(222),D3(32),D4(422),D6(622),图5点群432对称元素空间布置T(23)和O(432)共14种,其余18种为第二种.C2,C3和C4分别为2,3和4轴的一个位置空间点群的对称操作与平移对称操作(t过立方体某一棱边中点,放置平行于体对角线=m(n1a+n2b+n3c)/N,n1,n2和n3为整数;N为螺旋轴轴且长度为体对角线长的一段纱线(与xy坐标面夹角次;m为沿螺旋轴平移次数;a,b和c为以单胞边长的35°15′52″).以该段纱线为被操作客体,分别以群基矢量)组合形成空间群(不含纯镜面反射群元素的432(O)的群元素作对称操作,形成空间等效图案(图空间点群一定对应有编织空间群.单向增强纱线集6(a)),它由12根不同空间位置的纱线段组成;图6(b)合体和层合板中纱线的轴线也是直线,这里视为三为等效空间图案在6支2次旋转轴向的投影;图6(c)维编织的特殊方式).后一种则不一定.为图案在4支3次旋转轴向投影,图6(d)为图案在3需要指出,在与18种含有镜面反射对称操作空支4次旋转轴向投影,它们分别为相同的图案,具有间点群同态的空间群中,由于存在复合操作(即螺旋完全相同的对称性.旋转、滑移反射),对应空间群具有可对应编织几何结建立三维坐标系x,y和z,z向为4次对称轴方向.构的可能性,其中规律有待进一步加以研究.建立轴线与原始立方体重合,边长为2倍的新立方体,以三维四步法编织体为例,由空间点阵、点群到正好包络所有纱线段.其边长分别平行于坐标轴,边对应空间群推导三维编织几何结构.四步法编织的长设为H.在与平移群组合过程中,沿3支4次轴方单胞在理想情况下可取为立方体,这时不考虑编织向存在43次螺旋轴.对应平移群可以表示为载荷及实际工艺过程的特殊要求.从单纯考察其几3Γ={|tt=(nn123ab++nc),n1,n2和n3为整数,何结构的角度出发,不会对编织材料的性能分析造4成影响.||a||=||b||=||c||=H},6在立方点阵中,无论是取初基单胞或者惯用单空间群为P4332,用Schoenflies符号表示为O.胞都为立方体,而立方体与正八面体有相同的对称操对应的三维编织几何结构图6(e)所示.作.对称元素(点、线和面)包括对称轴(线)2,3和4次按照上述相同的过程,可由满足要求的编织空3种.即对应棱边中点连线的6支2次轴,对应相对间群推导对应的三维编织几何结构.表面的中心连线的4支3次轴;对应相对顶点的对角３结论线的3支4次轴,如图5所示.不考虑几何结构中对用点群和空间群描述编织材料,可以导出可能称操作的特殊性时,对应八面体群432(O),群的阶为的编织几何结构,并对其进行合理有效地分类,使得24.群元素有1c1(E),3c2(c2x,c2y,czx,),6c′2其类型不再局限于工艺上区分.编织空间群为编织(c2xy,c2xy,,c2xz,c2xz,c2yz,c2yz),8c3(c3xyz,体几何结构的推导提供了理论依据,为开发更多更−1−1−1−1c3xyz,c3xyz,c3xyz,c3xyz,c3xyz,c3xyz,c3xyz),为合理的编织物提供了系统有效的数学方法,可以6c(c,c−1,c,c−1,c,c−1).c−1表示处于大大丰富三维编织材料的品种,优化编织材料性能.44x4x4y4y4z4znxywww.scichina.com2303 第50卷第20期2005年10月论文图6用空间群P4332推导三维四步法编织几何结构(a)倾斜纱线段为无对称单元及空间点群432的对应空间等效图案,(b)图案在6支2次旋转轴向的投影,(c)图案在4支3次旋转轴向投影,(d)图案在3支4次旋转轴向投影,(e)对应空间群P4332的空间编织几何结构要研制成更多具有优异物理和力学综合性能的新编6WuDL.Three-cellmodeland5Dbraidedstructuralcomposites.织复合材料,人们尚需付出更多的辛勤劳动.CompositesScienceandTechnology,1996,56:225~233[DOI]7MouritzAP,BannisterMK,FalzonPJ,etal.Reviewofapplica-参考文献tionsforadvancedthree-dimensionalfibretextilecomposites.1SrirenganK,WhitcombJ,ChapmanC.ModaltechniqueforComposites:PartA,1999,30:1445~1461[DOI]three-dimensionalglobal/localstressanalysisofplainweave8ChenL,TaoXM,ChoyCL.Onthemicrostructureofcomposites.CompositesStructures,1997,39:145~156[DOI]three-dimensionalbraidedperforms.CompositesScienceand2ZemanJ,SejnohaM.HomogenizationofbalancedplainweaveTechnology,1999,59:391~404[DOI]compositeswithimperfectmicrostructure:PartI.Theoreticalfor-9ByunJH,WhitneyTJ,DuGW,etal.Analyticalcharacterizationmulation.InternationalJournalofSolidsandStructures,2004,41:oftwo-stepbraidedcomposites.JournalofCompositeMaterials,6549~6571[DOI]1991,25:1599~16183EverJB,ThomasMD,JonathanT,etal.Micromechanicsoffab-ricreinforcedcompositeswithperiodicmicrostructure.Interna-10李嘉禄,孙颖．二步法方型三维编织复合材料的细构．复合材tionalJournalofSolidsandStructures,2005,42:2489~2504[DOI]料学报,2002,19(4):69~754YangJM,MaCL,ChouTW.Fiberinclinationmodelofthree11王仁卉,郭可信．晶体学中的对称群．北京:科学出版社,1990.dimensionaltextilestructuralcomposites.JComposMater,1986,36~3820:472~48312LoeblEM.GroupTheoryanditsApplications.London:Acadmic5LiW,HammadM,El-ShieknA.Structuralanalysisof3-DbraidedPressIncLtd,1968.285~312preformsforcomposites,partone:Thefour-stepperforms.JText(2005-03-18收稿,2005-06-17收修改稿)Inst,1990,81:491~5142304www.scichina.com