达朗贝尔原理ppt课件.ppt 41页

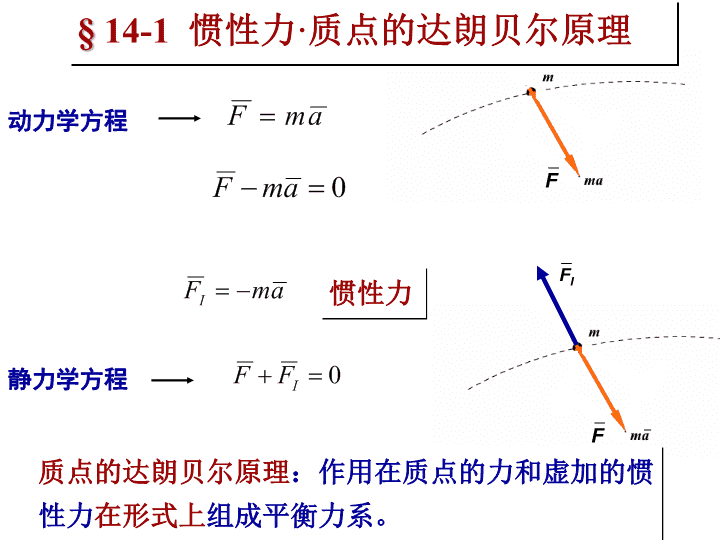
第十四章达朗贝尔原理(动静法) FFFI惯性力动力学方程静力学方程质点的达朗贝尔原理：作用在质点的力和虚加的惯性力在形式上组成平衡力系。§14-1惯性力·质点的达朗贝尔原理 §14-2质点系的达朗贝尔原理记为作用于第i个质点上外力的合力。为作用于第i个质点上内力的合力。则有质点系的达朗贝尔原理：质点系中每个质点上作用的力和它们的惯性力在形式上组成平衡力系。 因有质点系的达朗贝尔原理：作用在质点系上的外力与虚加在每个质点上的惯性力在形式上组成平衡力系。则有 §14-3　刚体惯性力系的简化１刚体平动惯性力系向质心简化。只简化为一个力惯性力主矢：注:对所有刚体均成立，对同一刚体向任意一点简化均成立质点系达朗贝尔原理：质心为合力作用点 2刚体定轴转动由有zx 记为对于z轴的惯性积。同理因有 如果刚体有质量对称面且该面与转动轴垂直,简化中心取此平面与转轴的交点，则有定轴转动刚体惯性力向轴心简化力：主矢力偶：主矩转轴通过质心,主矢为零匀速转动,主矩为零矢量沿转轴方向 ３　刚体作平面运动（平行于质量对称面运动，向质心简化） 向质心简化（主矢画在质心）通用公式各刚体 运动形式平动定轴转动平面运动惯性力（矩）加在质心加在转轴加在质心加在质心惯性力的添加方法注意主矢加的点和转动惯量下标协调 例如图所示均质杆的质量为m，长为l，绕定轴O转动的角速度为，角加速度为。求：惯性力系向点Ｏ及质心简化的结果（方向在图上画出）。 解：向轴心O简化 向质心C简化解： 名词：加惯性力（步骤、注意事项）1、判断运动形式2、加惯性力，判断质心运动，寻找质心加速度，直线、曲线、加在哪里3、加惯性力偶主矩转动惯量是关于哪个点的转动惯量4、写出惯性力和惯性矩的表达式表达式不应再加负号注意主矢加的点和转动惯量下标协调 典型错误之一Oα注意转动惯量与惯性力所加位置的协调× 典型错误之二只有定轴转动惯性力可以加在轴心和质心2点，平面运动刚体只能加在质心Oαα加惯性力之前应注意刚体做什么运动，只有定轴转动可以加在端点转轴，平面运动不行× αααω给下列刚体添加惯性力α纯滚动 图为一电动卷扬机构的示意图。已知起动时电动机的平均驱动力矩为M，被提升重物的质量为m1，鼓轮质量为m2，半径为r，它对中心的回转半径为ρO。试求起动时重物的平均加速度a和此时轴承O的动约束力。xyαMrm1gaOm2g 3、列平面力系平衡方程重物作平动鼓轮绕质心作定轴转动xyMF*M*Crm1gαaOFOxFOym2g解：1、研究对象取整体2、实际受力分析3、运动分析加惯性力（假设加速度、角加速度）4、补充方程 xyαMF*M*Crm1gaOFOxFOym2g 用长l的两根绳子AO和BO把长l，质量是m的匀质细杆悬在点O(图a)。当杆静止时，突然剪断绳子BO，试求刚剪断瞬时另一绳子AO的拉力。OlllBAC例题 加惯性力，注意质心轨迹且对于细杆,JCz´=ml2／12。联立求解方程(1)～(4)，就可求出（2）（3）（4）OllBACmgFθxy（1）受力分析，运动分析，AB将在铅直面内作平面运动。α anA+atA=aCx+aCy+atAC+anACOxyαBACθ以杆AB为研究对象利用刚体作平面运动的加速度合成定理，以质心C作基点，则点A的加速度为绳BO刚剪断瞬时，杆角速度ω=0，角加速度α≠0。把aA投影到点A轨迹的法线AO上anAC=0atAC=lα／2（1）anA=0aA=aC+atAC+anAC 名词：动静法（解题步骤、注意事项）1、确定研究对象，进行实际受力分析3、运用静力学平衡方程求解，注意添加补充方程2、运动分析加惯性力，写出惯性力表达式切记不能丢力，特别是重力约束力，都应清楚地画在图中（多刚体问题加速度应协调，最好先假设） 典型错误之三OlllBACGFFIOllBACmgFθxyα 由动静法，受力分析加惯性力（2）（3）（4）OllBACmgFθxy写杆的平衡方程α惯性力必须写成加速度的形式才能寻找运动学补充方程，不能直接把惯性力作为未知量来求解。惯性力加完，马上写出其表达式，带入方程典型错误之四 MFIMIaαFBxBGG2FBx例题：匀质悬臂梁AB长l，重G1，匀质圆轮B重G，半径r，在轮上作用一力偶M，重物D重G2，试求固定端A的约束力和约束力偶。解：1、选研究对象如图外力分析运动分析加惯性力lABDM列静力学方程补充方程 ABMFIMIaαGG1G2FAxFAyMA解得：2、以整体为研究对象 FFFI惯性力动力学方程静力学方程 求解动力学问题的基本方法1、动力学方法（动量定理，动量矩定理）2、能量的方法（动能定理，机械能守恒，功率方程）3、动静法 由动静法，受力分析加惯性力且对于细杆,JCz´=ml2／12。联立求解方程(1)～(4)，就可求出（2）（3）（4）OllBACmgFθxy（1）写杆的平衡方程绳子BO剪断后，杆AB将在铅直面内作平面运动。α 且对于细杆,JCz´=ml2／12。联立求解方程(1)～(4)，就可求出OllBACmgFθxy绳子BO剪断后，杆AB将在铅直面内作平面运动。α 动量法动静法 由动静法，受力分析加惯性力OllBACmgFθxyα典型错误之五注意动静法与动力学方法区别1是有没有加惯性力2是方程为平衡方程，一侧为0。 动力学基本知识运动形式平动定轴转动平面运动动量动量矩对任意点（对转轴）（对质心）动能(O为转轴）惯性力（矩）加在质心加在转轴加在质心加在质心适用动力学方程(O为转轴）定轴转动和平面运动对除质心和轴心外的点的动量矩用主矩定理。 第14-4绕定轴转动刚体的轴承动约束力 解得 即：必有通过质心的惯性主轴称为中心惯性主轴因此，避免出现轴承动约束力的条件是：刚体的转轴应是刚体的中心惯性主轴。引起的轴承约束力称动约束力，由称满足的轴z为惯性主轴动约束力为零的条件为： 例14-8如图所示,轮盘(连同轴)的质量转轴AB与轮盘的质量对称面垂直,但轮盘的质心C不在转轴上,　偏心距　　　　　当轮盘以均转速转动时。求：轴承A,B的约束力 解：