内蒙古呼伦贝尔市高三数学总复习《三角函数的图象和性质》课件.ppt 90页

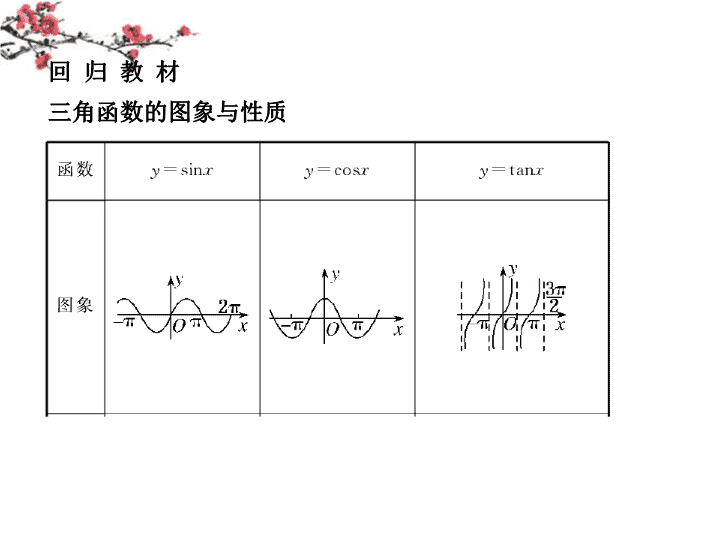
第二十九讲三角函数的图象和性质1 走进高考第一关考点关 回归教材三角函数的图象与性质 (以上表中k∈Z) 注意:(1)三角函数奇偶性的判断与代数函数奇偶性的判断步骤一致:①首先看定义域是否关于原点对称.②在满足①的前提下再看f(-x)与f(x)的关系.另外三角函数中奇函数一般可化为y=Asinωx或y=Atanωx,偶函数一般可化为y=Acosωx+b的形式. 考点训练提示:由五点作图法可知答案为A.答案:A 解析:逐个检验.答案:D 答案:A 答案:C 答案:B 解读高考第二关热点关 题型一三角函数的图象例1 描出对应的五点(x,y),用光滑曲线连结各点即得所做函数的图象. (2)图象变换有两种方式:①先平移后伸缩;②先伸缩后平移,要注意两种变换下的平移量的大小不同. 答案:C 题型二有关三角函数的解析式 点评:对于由y=Asin(ωx+φ)+k的图象,求其解析式的问题,主要从以下四个方面考虑:(4)φ的确定:由函数y=Asin(ωx+φ)+k通过特殊点确定φ. 变式2:下列函数中,图象的一部分如图所示的是()答案:D 题型三有关三角函数的最值问题 点评:三角函数求最值常见的有如下几种形式:(1)可化为形如y=asinx+bcosx,可利用化一公式求解;(2)对于形如y=asin2x+bsinxcosx+ccos2x形式,可先降次,再求解 题型四三角函数的性质例4 (1)求函数f(x)的最小正周期及最值;(2)写出f(x)的单调增区间; (2)对于函数的奇偶性,应先判定函数的定义域是否关于坐标原点对称,再看f(-x)等于什么,从而断定函数的奇偶性。(3)对于三角函数单调区间的确定,一般先将函数转化为基本三角函数的标准形式,利用公式求解. 笑对高考第三关技巧关三角函数的图象和性质是高考的热点之一,其性质与图象有着内在的联系.如:①正弦曲线,余弦曲线的对称轴恰经过相应曲线的最高点或最低点,相邻两对称轴之间函数的单调性相同并且相邻两对称轴之间的距离恰等于函数的半个周期;②正弦曲线,余弦曲线的对称中心分别是正弦函数和余弦函数的零点(与x轴的交点),相邻两对称中心之间的距离也恰好是函数的半个周期,并且对称轴,对称中心间隔排列着;③正切曲线的对称中心除去零点外还有使正切函数值不存在的点,用平行于x轴的直线去截正切曲线,相邻两交点之间的距离相等并且都等于正切函数的周期. 答案:0点评:掌握三角函数的图象与性质是解决此类问题的关键. 考向精测答案:C 答案:D 课时作业(二十九)三角函数的图象和性质 第一课时一、选择题答案:D 2.已知f(x)=2sin(ωx+φ)的图象如下图所示,则f(x)的表达式为() 答案:B 答案:A 答案:D 答案:D 答案:D 二、填空题7.(2009·辽宁)已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则ω=________. 三、解答题(1)求m,n的值;(2)若f(x)=2,求x的值. 第二课时 一、选择题答案:A 答案:B 答案:A 解析:逐个检验.答案:D 答案:A 答案:A 解析:逐个检验.答案:A 二、填空题 答案:①②③ 答案:a