呼伦贝尔市八年级数学试卷易错压轴选择题精选：平行四边形选择题试题(及答案)(2) 37页

呼伦贝尔市八年级数学试卷易错压轴选择题精选：平行四边形选择题试题(及答案)(2)一、易错压轴选择题精选：平行四边形选择题1．如图，在菱形ABCD中，AB＝BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE＝DF，连接BF与DE相交于点G，连接CG与BD相交于点H.给出如下几个结32论：①△AED≌△DFB：②GC平分∠BGD；③S四边形BCDG＝CG；④∠BGE的大小为定4值．其中正确的结论个数为（）A．1B．2C．3D．42．如图，△ABC中，AB＝24，BC＝26，CA＝14．顺次连接△ABC各边中点，得到△A1B1C1；再顺次连接△A1B1C1各边中点，得到△A2B2C2⋯如此进行下去，得到AnBnCn，则△A8B8C8的周长为（）111A．1B．C．D．2483．如图，一个四边形花坛ABCD，被两条线段MN,EF分成四个部分，分别种上红、黄、紫、白四种花卉，种植面积依次是S1、S2、S3、S4，若MN∥AB∥DC，EF∥DA∥CB，则有（）A．S1=S4B．S1+S4=S2+S3C．S1+S3=S2+S4D．S1·S4=S2·S34．如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②△APD一定是等腰三角形；③AP⊥EF；2④PD=EF．其中正确结论的番号是（）2 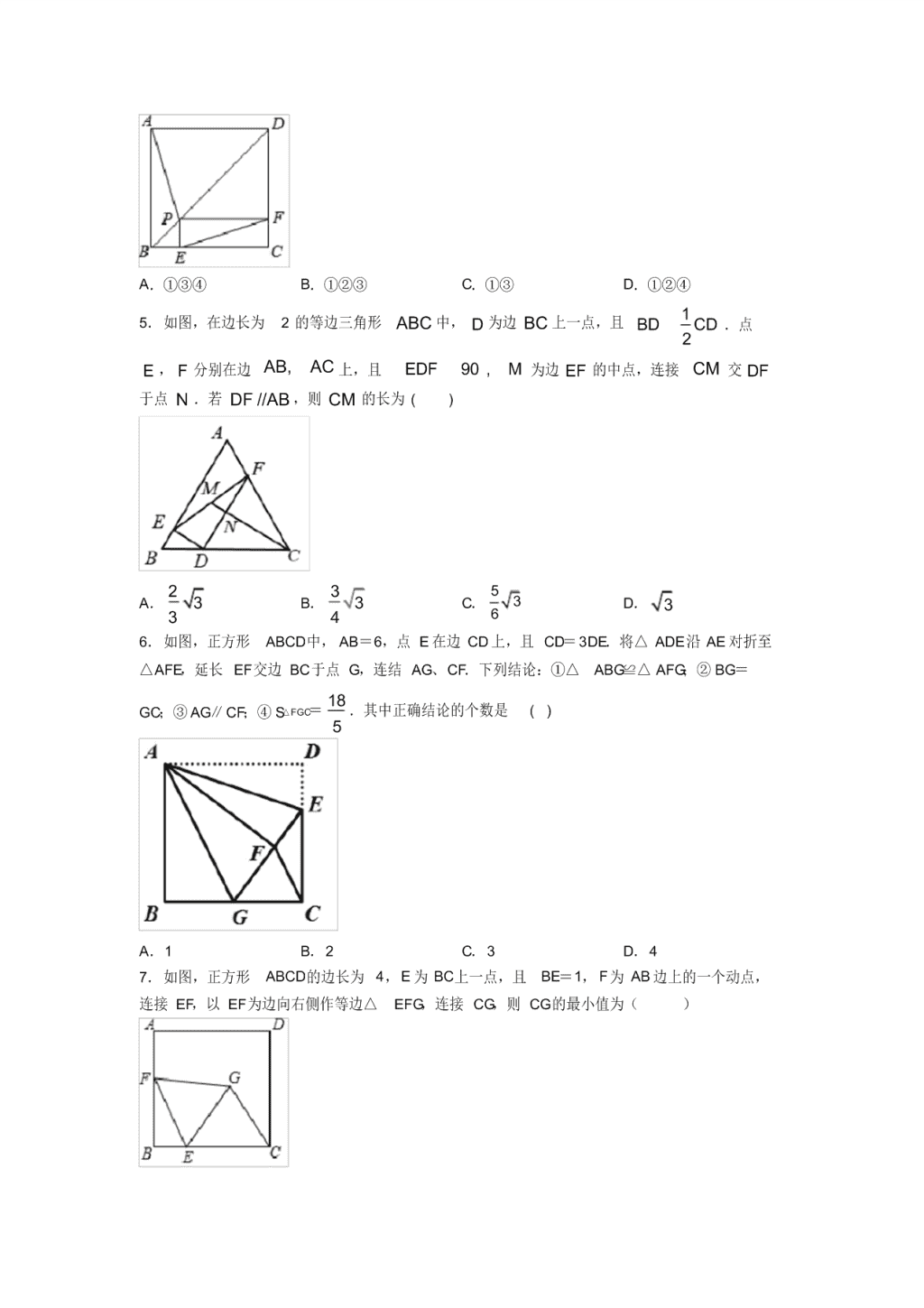A．①③④B．①②③C．①③D．①②④15．如图，在边长为2的等边三角形ABC中，D为边BC上一点，且BDCD．点2E，F分别在边AB,AC上，且EDF90,M为边EF的中点，连接CM交DF于点N．若DF//AB，则CM的长为()235A．3B．3C．3D．33466．如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG＝18GC；③AG∥CF；④S△FGC＝．其中正确结论的个数是()5A．1B．2C．3D．47．如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为（） A．0.5B．2.5C．2D．18．如图，矩形ABCD的对角线AC、BD交于点O，点P在边AD上从点A到点D运动，过点P作PE⊥AC于点E，作PF⊥BD于点F，已知AB=3，AD=4，随着点P的运动，关于PE+PF的值，下面说法正确的是（）A．先增大，后减小B．先减小，后增大C．始终等于2.4D．始终等于39．如图，正方形ABCD中，延长CB至E使CB2EB，以EB为边作正方形EFGB，延长FG交DC于M，连接AM，AF，H为AD的中点，连接FH分别与AB，AM交于点N,K．则下列说法：①△ANH≌△GNF；②DAMNFG；③FN2NK；④S△AFN:S四边形DMKH2:7．其中正确的有（）A．4个B．3个C．2个D．1个10．在菱形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的一点(不与端点重合)，对于任意的菱形ABCD，下面四个结论中：①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形正确的结论的个数是()A．1个B．2个C．3个D．4个11．如图，在RtABC中，ACB90，分别以AB，AC，BC为边，在AB的同侧作正方形ABHI，ACFG，BCED．若图中两块阴影部分的面积分别记为S1，S2，则对S1，S2的大小判断正确的是（）A．S1S2B．S1S2C．S1S2D．无法确定 12．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（）533A．2B．C．D．52213．如图，MON90，矩形ABCD在MON的内部，顶点A，B分别在射线OM，ON上，AB4，BC2，则点D到点O的最大距离是（）A．222B．222C．252D．2214．在ABCF中，BC2AB，CDAB于点D，点E为AF的中点，若ADE50，则B的度数是（）A．50B．60C．70D．8015．如图，矩形ABCD中，AB＝10，AD＝4，点E从D向C以每秒1个单位的速度运动，以AE为一边在AE的左上方作正方形AEFG，同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动，当点F落在直线MN上，设运动的时间为t，则t的值为()1014A．1B．C．4D．33 16．如图，在ABC中，AB=AC=6，∠B=45°，D是BC上一个动点，连接AD，以AD为边向右侧作等腰ADE，其中AD=AE，∠ADE=45°，连接CE．在点D从点B向点C运动过程中，△CDE周长的最小值是（）A．62B．626C．92D．926117．如图，平行四边形ABCD中，对角线AC、BD相交于点O，AD＝AC，M、N、P分别2是OA、OB、CD的中点，下列结论：①CN⊥BD；②MN＝NP；③四边形MNCP是菱形；④ND平分∠PNM．其中正确的有（）A．1个B．2个C．3个D．4个18．如图，点P，Q分别是菱形ABCD的边AD，BC上的两个动点，若线段PQ长的最大值为85，最小值为8，则菱形ABCD的边长为()A．46B．10C．12D．1619．如图的△ABC中，AB>AC>BC,且D为BC上一点．现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等，以下是甲、乙两人的作法：甲：连接AD,作AD的中垂线分别交AB、AC于P点、Q点，则P、Q两点即为所求；乙：过D作与AC平行的直线交AB于P点，过D作与AB平行的直线交AC于Q点，则P、Q两点即为所求；对于甲、乙两人的作法，下列判断何者正确（） A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误乙正确20．如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（）A．2.8B．22C．2.4D．3.521．如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB=90°，且BC=2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3，若S1=3，S3=8，则S2的值为（）A．22B．24C．44D．4822．下列命题中，真命题的个数有（）①对角线相等的四边形是矩形；②三条边相等的四边形是菱形；③一组对边平行且相等的四边形是平行四边形．A．3个B．2个C．1个D．0个23．如图，已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（10，0），点B（0，6），点P为BC边上的动点，将△OBP沿OP折叠得到△OPD，连接CD、AD．则下列结论中：①当∠BOP＝45°时，四边形OBPD为正方形；②当∠BOP＝30°时，△OAD的面积为15；③当P在运动过程中，CD的最小值为234﹣6；④当OD⊥AD时，BP＝2．其中结论正确的有（） A．1个B．2个C．3个D．4个24．如图，在ABC中，AB=5，AC=12，BC=13，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为（）60302412A．B．C．D．1313131325．如图，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC=EC，连结DF交BE的延长线于点H，连结OH交DC于点G，连结HC．则以下四个结论1中：①OH∥BF，②GH=BC，③BF=2OD，④∠CHF=45°．正确结论的个数为()4A．4个B．3个C．2个D．1个26．如图，将边长为8cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在点F处，折痕为MN，则折痕MN的长是（）A．53cmB．55cmC．46cmD．45cm27．如图，在△ABC中，∠ABC和∠ACB的角平分线相交于点O．过点O作EF∥BC交AB于E．交AC于F．过点O作OD⊥AC于D．下列五个结论：其中正确的有（）1（1）EF=BE+CF；（2）∠BOC=90°+∠A；（3）点O到△ABC各边的距离都相等；2（4）设OD=m．若AE十AF=n，则S△AEF=mn；（5）S△AEF=S△FOC． A．2个B．3个C．4个D．5个28．如图，在边长为6的正方形ABCD中，E是边CD的中点，将ADE沿AE对折至AFE，延长交BC于点G，连接AG.则BG的长（）A．1B．2C．3D．329．如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA1A2B1，⋯，依此规律，则点A8的坐标是（）A．（－8，0）B．（0，8）C．（0，82）D．（0，16）30．如图，在△ABC中，AB＝3，AC＝4，BC＝5，△ABD，△ACE，△BCF都是等边三角形，下列结论中：①AB⊥AC；②四边形AEFD是平行四边形；③∠DFE＝150°；④S四边形AEFD＝5．正确的个数是（）A．1个B．2个C．3个D．4个 【参考答案】***试卷处理标记，请不要删除一、易错压轴选择题精选：平行四边形选择题1．D【分析】①先证明△ABD为等边三角形,根据“SAS”证明△AED≌△DFB;②证明∠BGE＝60＝∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC＝∠DGC＝60;③过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG＝S四边形CMGN,易求后者的面积;④∠BGE＝∠BDG+∠DBF＝∠BDG+∠GDF＝60,故为定值.【详解】解：①∵ABCD为菱形,∴AB＝AD,∵AB＝BD,∴△ABD为等边三角形,∴∠A＝∠BDF＝60又∵AE＝DF,AD＝BD,∴△AED≌△DFB（SAS）,故本选项正确;②∵∠BGE＝∠BDG+∠DBF＝∠BDG+∠GDF＝60＝∠BCD,即∠BGD+∠BCD＝180,∴点B、C、D、G四点共圆,∴∠BGC＝∠BDC＝60,∠DGC＝∠DBC＝60,∴∠BGC＝∠DGC＝60,故本选项正确;③过点C作CM⊥GB于M,CN⊥GD于N（如图）,则△CBM≌△CDN（AAS）,∴S四边形BCDG＝S四边形CMGNS四边形CMGN＝2S△CMG,∵∠CGM＝60,13∴GM＝CG,CM＝CG,22 11332∴S四边形CMGN＝2S△CMG＝2××CG×CG＝CG,2224故本选项正确;④∵∠BGE＝∠BDG+∠DBF＝∠BDG+∠GDF＝60,为定值,故本选项正确;综上所述,正确的结论有①②③④,故选：D.【点睛】本题考查了菱形的性质、全等三角形的判定、等边三角形的判定与性质,解决本题的关键是掌握菱形的性质．2．C【分析】根据三角形中位线定理求出△A1B1C1的周长，根据计算总结规律，根据规律解答.【详解】根据三角形中位线定理求出△A1B1C1的周长，根据计算结果总结规律，根据规律解答．解：∵A1、C1分别为AB、AC的中点，∴A1C1＝BC＝13，11同理，A1B1＝AC＝7，B1C1＝AB＝12，22∴△A1B1C1的周长＝7+12+13＝32，1∴△A1B1C1的周长＝△ABC的周长×，2112则△A2B2C2的周长＝△A1B1C1的周长×＝△ABC的周长×（），22⋯⋯1118∴△A8B8C8的周长＝△ABC的周长×（）＝64×＝，22564故选：C．【点睛】本题考查三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键.3．D【分析】由于在四边形中，MN∥AB∥DC，EF∥DA∥CB，因此MN、EF把一个平行四边形分割成四个小平行四边形．可设MN到DC的距离为h1，MN到AB的距离为h2，根据AB=CD，DE=AF，EC=FB及平行四边形的面积公式即可得出答案．【详解】解：∵MN∥AB∥DC，EF∥DA∥CB，∴四边形ABCD，四边形ADEF，四边形BCEF，红、紫、黄、白四边形都为平行四边形， ∴AB=CD，DE=AF，EC=BF．设MN到DC的距离为h1，MN到AB的距离为h2，则S1=DE?h1，S2=AF?h2，S3=EC?h1，S4=FB?h2，因为DE，h1，FB，h2的关系不确定，所以S1与S4的关系无法确定，故A错误；S1+S4=DE?h1+FB?h2=AF?h1+FB?h2，S2+S3=AF?h2+EC?h1=AF?h2+FB?h1，故B错误；S1+S3=CD?h1，S2+S4=AB?h2，又AB=CD，而h1不一定与h2相等，故C错误；S1·S4=DE?h1?FB?h2=AF?h1?FB?h2，S2·S3=AF?h2?EC?h1=AF?h2?FB?h1，所以S1·S4=S2·S3，故D正确；故选：D．【点睛】本题考查平行四边形的判定与性质，注意掌握平行四边形的面积等于平行四边形的边长与该边上的高的积．即S=a?h．其中a可以是平行四边形的任何一边，h必须是a边与其对边的距离，即对应的高．4．C【分析】过P作PG⊥AB于点G，根据正方形对角线的性质及题中的已知条件，证明△AGP≌△FPE后即可证明①AP=EF；在此基础上，根据正方形的对角线平分对角的性质，在Rt△DPF中，2222222DP=DF+PF=EC+EC=2EC，求得DPEC，即可得到答案．2【详解】证明：过P作PG⊥AB于点G，∵点P是正方形ABCD的对角线BD上一点，∴GP=EP，在△GPB中，∠GBP=45°，∴∠GPB=45°，∴GB=GP，同理，得PE=BE，∵AB=BC=GF，∴AG=AB-GB，FP=GF-GP=AB-GB，∴AG=PF，∴△AGP≌△FPE，∴AP=EF；故①正确；延长AP到EF上于一点H， ∴∠PAG=∠PFH，∵∠APG=∠FPH，∴∠PHF=∠PGA=90°，即AP⊥EF；故③正确；∵点P是正方形ABCD的对角线BD上任意一点，∠ADP=45度，∴当∠PAD=45度或67.5度或90度时，△APD是等腰三角形，除此之外，△APD不是等腰三角形，故②错误．∵GF∥BC，∴∠DPF=∠DBC，又∵∠DPF=∠DBC=45°，∴∠PDF=∠DPF=45°，∴PF=EC，222222∴在Rt△DPF中，DP=DF+PF=EC+EC=2EC，2∴DPEC，故④错误．2∴正确的选项是①③；故选：C．【点睛】本题考查了正方形的性质，全等三角形的判定及性质，垂直的判定，等腰三角形的性质，勾股定理的运用．本题难度较大，综合性较强，在解答时要认真审题．5．C【分析】根据等边三角形边长为2，在RtBDE中求得DE的长，再根据CM垂直平分DF，在RtCDN中求得CN，利用三角形中位线求得MN的长，最后根据线段和可得CM的长．【详解】1解：等边三角形边长为2，BDCD，224∴BD，CD，33等边三角形ABC中，DF//AB，FDCB60，EDF90，BDE30，DEBE，211222123BEBD，DEBDBE()，233331如图，连接DM，则RtDEF中，DMEFFM，2 FDCFCD60，CDF是等边三角形，4CDCF，3CM垂直平分DF，DCN30，4223RtCDN中，DF，DN，CN，333∵EM=FM，DN=FN，13∴MNED，2623353CMCNMN．366故选：C．【点睛】本题主要考查了三角形的综合应用，解决问题的关键是掌握等边三角形的性质、勾股定理、平行线的性质、线段垂直平分线的判定等．熟练掌握这些性质是解题的关键．6．D【分析】由正方形和折叠的性质得出AF＝AB，∠B＝∠AFG＝90°，由HL即可证明Rt△ABG≌Rt△AFG，得出①正确；设BG＝x，则CG＝BC-BG＝6-x，GE＝GF＋EF＝BG＋DE＝x＋2，由勾股定理求出x＝3，得出②正确；由等腰三角形的性质和外角关系得出∠AGB＝∠FCG，证出平行线，得出③正确；18根据三角形的特点及面积公式求出△FGC的面积＝，得出④正确．5【详解】∵四边形ABCD是正方形，∴AB＝AD＝DC＝6，∠B＝D＝90°，∵CD＝3DE，∴DE＝2，∵△ADE沿AE折叠得到△AFE，∴DE＝EF＝2，AD＝AF，∠D＝∠AFE＝∠AFG＝90°，∴AF＝AB， ∵在Rt△ABG和Rt△AFG中，AGAG，ABAF∴Rt△ABG≌Rt△AFG（HL），∴①正确；∵Rt△ABG≌Rt△AFG，∴BG＝FG，∠AGB＝∠AGF，设BG＝x，则CG＝BC-BG＝6-x，GE＝GF＋EF＝BG＋DE＝x＋2，222在Rt△ECG中，由勾股定理得：CG＋CE＝EG，∵CG＝6-x，CE＝4，EG＝x＋2222∴（6-x）＋4＝（x＋2）解得：x＝3，∴BG＝GF＝CG＝3，∴②正确；∵CG＝GF，∴∠CFG＝∠FCG，∵∠BGF＝∠CFG＋∠FCG，又∵∠BGF＝∠AGB＋∠AGF，∴∠CFG＋∠FCG＝∠AGB＋∠AGF，∵∠AGB＝∠AGF，∠CFG＝∠FCG，∴∠AGB＝∠FCG，∴AG∥CF，∴③正确；∵△CFG和△CEG中，分别把FG和GE看作底边，则这两个三角形的高相同．SCFGFG3∴，SCEGGE51∵S△GCE＝×3×4＝6，2318∴S△CFG＝×6＝，55∴④正确；正确的结论有4个，故选：D．【点睛】本题考查了正方形性质、折叠性质、全等三角形的性质和判定、等腰三角形的性质和判定、平行线的判定等知识点的运用；主要考查学生综合运用性质进行推理论证与计算的能力，有一定难度．7．B 【分析】由题意分析可知，点F为主动点，G为从动点，所以以点E为旋转中心构造全等关系，得到点G的运动轨迹，之后通过垂线段最短构造直角三角形获得CG最小值．【详解】由题意可知，点F是主动点，点G是从动点，点F在线段上运动，点G也一定在直线轨迹上运动，如图，将ΔEFB绕点E旋转60°，使EF与EG重合，得到ΔEFB?ΔEHG，从而可知ΔEBH为等边三角形，点G在垂直于HE的直线HN上，如图，作CM⊥HN，则CM即为CG的最小值，作EP⊥CM，可知四边形HEPM为矩形，135则CMMPCPHEEC1=2.5.222故选B．【点睛】本题考查了线段极值问题，构造图形计算，是极值问题中比较典型的类型．分清主动点和从动点，通过旋转构造全等，从而判断出点G的运动轨迹，是解本题的关键．8．C【分析】1在矩形ABCD中，由矩形边长，可得矩形面积是12，进而得SAODS矩形ABCD3，由矩4形对角线相等且互相平分得AOOC，OBOD，ACBD，利用勾股定理可解得5AC5,则OAOD，2111SAODSAOPSDOPOAPEODPFOA(PEPF)3，即可求出PE+PF222的值．【详解】解：连接PO，如下图： ∵在矩形ABCD中，AB=3，AD=4，∴S矩形ABCDABBC12,AOOC，OBOD，ACBD，22AC=AB+BC=5，11∴SAODS矩形ABCD123,445OAOD，211115SAODSAOPSDOPOAPEODPFOA(PEPF)(PEPF)322222，12∴PEPF2.4；5故选C．【点睛】本题主要考查了矩形的性质，利用等积法间接求三角形的高线长及用勾股定理求直角三角形的斜边；利用面积法求解，是本题的解题突破点．9．A【分析】根据正方形的性质，以及中点的性质可得△FGN≌△HAN，即证①；利用角度之间的等量关系的转换可以判断②；根据△AKH∽△MKF，进而利用相似三角形的性质即可判断③；1AH2x1设AN=AG=x，则AH=2x，FM=6x，根据△AKH∽△MKF得出，再利用三2MF6x3角形的面积公式求出△AFN的面积，再利用SDHKMSADMSAKH即可求出四边形DHKM的面积，作比即可判断④．【详解】∵四边形EFGB是正方形，CE=2EB，四边形ABCD是正方形∴G为AB中点，∠FGN=∠HAN=90°，AD=AB1即FG=AG=GB=AB2又H是AD的中点1AH=AD2 ∴FG=HA又∠FNG=∠HNA∴△FGN≌△HAN，故①正确；∵∠DAM+∠GAM=90°又∠NFG+∠FNG=90°即∠FNG=∠GAM∵∠FNG+∠NFG+90°=180°∠AMD+∠DAM+90°=180°∠FNG=∠GAM=∠AMD∴DAMNFG，故②正确；由图可得：MF=FG+MG=3EB△AKH∽△MKFKHAH1∴KFMF3∴KF=3KH又∵NH=NF且FH=KF+KH=4KH=NH+NF∴NH=NF=2KH∴KH=KN∴FN=2NK，故③正确；∵AN=GN且AN+GN=AG1∴可设AN=AG=x，则AH=2x，FM=6x2AH2x1由题意可得：△AKH∽△MKF且相似比为：MF6x311∴△AKH以AH为底边的高为：2xx4212∴SAFNANFGx2112SDHKMSADMSAKHADDMAHx225111722x4x2xxx22222∴SAFN:SDHKM，故④正确；7故答案选择A．【点睛】本题考查了矩形、全等三角形的判定与性质以及相似三角形的判定与性质，难度较大，需要熟练掌握相关基础知识．10．D 【分析】根据菱形的判定和性质，矩形的判定，正方形的判定，平行四边形的判定定理即可得到结论．【详解】①如图，连接AC，BD交于O，四边形ABCD是菱形，过点O直线MP和QN，分别交AB，BC，CD，AD于M，N，P，Q，则四边形MNPQ是平行四边形，故存在无数个四边形MNPQ是平行四边形；故正确；②如图，当PM=QN时，四边形MNPQ是矩形，故存在无数个四边形MNPQ是矩形；故正确；③如图，当PM⊥QN时，存在无数个四边形MNPQ是菱形；故正确；④如图，当四边形ABCD为正方形时，四边形MNPQ是正方形，故至少存在一个四边形MNPQ是正方形；故④正确；综上，①②③④4个均正确，故选：D．【点睛】本题考查了平行四边形的判定和性质，菱形的判定，正方形的判定，矩形的判定，熟记各定理是解题的关键． 11．B【分析】连接EH，过点H作HK⊥BF于点K，令AE与BH交于点J，HL与BF交于点L，根据已知条件易证△BHK≌△ABC，继而由全等三角形的性质得S△BHK＝S△ABC，BC＝HK，∠ABC＝∠BHK，再由全等三角形的判定可得△BCJ≌△HKL，进而可得S1＝S△BHK＝S△ABC，由正方形的性质和全等三角形的判定可知△ABC≌△AIG，继而可得S△ABC＝S△AIG＝S2，等量代换即可求解．【详解】解：连接EH，过点H作HK⊥BF于点K，令AE与BH交于点J，HL与BF交于点L，由题意可知：四边形BCED是正方形，四边形ACFG是正方形，四边形ABHI是正方形，∠ACB＝90°∴∠CEH＝∠ECK＝90°,CE＝BC∵∠BKH＝90°,∴四边形CEHK是矩形，∴CE＝HK又∠HBK＋∠ABC＝90°,∠BAC＋∠ABC＝90°∴∠HBK＝∠BAC∴△BHK≌△ABC（AAS）∴S△BHK＝S△ABC，BC＝HK，∠ABC＝∠BHK，∵∠ABC＋∠CBJ＝90°，∠BHK＋∠KHL＝90°∴∠CBJ＝∠KHL∴△BCJ≌△HKL（ASA）∴S△BCJ＝S△HKL，∴S1＝S△BHK＝S△ABC，∵四边形ACFG是正方形，四边形ABHI是正方形，∴AB＝AI，AC＝AG，∠G＝∠ACB＝90°∴△ABC≌△AIG（SAS）∴S△ABC＝S△AIG＝S2，即S1＝S2故选：B【点睛】本题主要考查正方形的性质，全等三角形的判定及其性质，解题的关键是熟练掌握正方形 的性质及全等三角形的判定方法．12．D【分析】根据正方形的性质得到AB=BC=1，CE=EF=3，∠E=90°，延长AD交EF于M，连接AC、CF，1求出∠ACF=90°，得到CH=AF，根据勾股定理求出AF的长度即可得到答案.2【详解】∵正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，∴AB=BC=1，CE=EF=3，∠E=90°，延长AD交EF于M，连接AC、CF，则AM=BC+CE=1+3=4，FM=EF-AB=3-1=2，∠AMF=90°，∵四边形ABCD和四边形GCEF是正方形，∴∠ACD=∠GCF=45°，∴∠ACF=90°，∵H为AF的中点，1∴CH=AF，2在Rt△AMF中，由勾股定理得：AF=2222，AMMF4225∴CH=5，故选：D．【点睛】此题考查了正方形的性质，勾股定理，直角三角形斜边上的中线等于斜边一半的性质，正确引出辅助线得到∠ACF=90°是解题的关键.13．B【分析】取DC的中点E，连接OE、DE、OD，根据三角形的任意两边之和大于第三边可知当O、E、D三点共线时，点D到点O的距离最大，再根据勾股定理求出DE的长，根据直角三角形斜边上的中线等于斜边的一半求出OE的长，两者相加即可得解．【详解】取AB中点E，连接OE、DE、OD，MON90，1OEAB2．2 在RtDAE中，利用勾股定理可得DE22．在ODE中，根据三角形三边关系可知DEOEOD，当O、E、D三点共线时，OD最大为OEDE222．故选B．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半得到性质，三角形的三边关系，矩形的性质，勾股定理，根据三角形的三边关系判断出点O、E、D三点共线时，点D到点O的距离最大是解题的关键．14．D【分析】连结CE，并延长CE，交BA的延长线于点N，根据已知条件和平行四边形的性质可证明△NAE≌△CFE，所以NE＝CE，NA＝CF，再由已知条件CD⊥AB于D，∠ADE＝50°，即可求出∠B的度数．【详解】解：连结CE，并延长CE，交BA的延长线于点N，∵四边形ABCF是平行四边形，∴AB∥CF，AB＝CF，∴∠NAE＝∠F，∵点E是的AF中点，∴AE＝FE，在△NAE和△CFE中，NAEFAEFE，AENFEC∴△NAE≌△CFE（ASA）， ∴NE＝CE，NA＝CF，∵AB＝CF，∴NA＝AB，即BN＝2AB，∵BC＝2AB，∴BC＝BN，∠N＝∠NCB，∵CD⊥AB于D，即∠NDC＝90°且NE＝CE，1∴DE＝NC＝NE，2∴∠N＝∠NDE＝50°＝∠NCB，∴∠B＝80°．故选：D．【点睛】本题考查了平行四边形的性质，综合性较强，难度较大，解答本题的关键是正确作出辅助线，构造全等三角形，在利用等腰三角形的性质解答．15．D【分析】过点F作FH⊥CD，交直线CD于点Q，则∠EHF=90°，易证∠ADE=∠EHF，由正方形的性质得出∠AEF=90°，AE=EF，证得∠AED=∠EFH，由AAS证得△ADE≌△EHF得出AD=EH=4，则t+2t=4+10，即可得出结果．【详解】过点F作FH⊥CD，交直线CD于点Q，则∠EHF=90°，如图所示：∵四边形ABCD为矩形，∴∠ADE=90°，∴∠ADE=∠EHF，∵在正方形AEFG中，∠AEF=90°，AE=EF，∴∠AED+∠HEF=90°，∵∠HEF+∠EFH=90°，∴∠AED=∠EFH，在△ADE和△EHF中， ADE＝EHFAED＝EFH，AE＝EF∴△ADE≌△EHF（AAS），∴AD=EH=4，由题意得：t+2t=4+10，14解得：t=，3故选D．【点睛】本题考查了正方形的性质、矩形的性质、全等三角形的判定与性质等知识，熟练掌握正方形与矩形的性质，通过作辅助线证明三角形全等是解题的关键．16．B【分析】如图（见解析），先根据等腰直角三角形的判定与性质可得BACDAE90,BC62,DE2AD，再根据三角形全等的判定定理与性质可得BDCE，从而可得△CDE周长为BC2AD，然后根据垂线段最短可求出AD的最小值，由此即可得．【详解】在ABC中，ABAC6,B45，22ABC是等腰直角三角形，BAC90,BCABAC62，在ADE中，ADAE,ADE45，22ADE是等腰直角三角形，DAE90,DEADAE2AD，BADCADCAECAD90，BADCAE，ABAC在△ABD和△ACE中，BADCAE，ADAEABDACE(SAS)，BDCE，CDE周长为CDCEDECDBDDEBCDE622AD，则当AD取得最小值时，△CDE的周长最小，由垂线段最短可知，当ADBC时，AD取得最小值，AD是BC边上的中线（等腰三角形的三线合一），1ADBC32（直角三角形斜边上的中线等于斜边的一半），2 CDE周长的最小值为62232626，故选：B．【点睛】本题考查了等腰直角三角形的判定与性质、直角三角形斜边上的中线、三角形全等的判定定理与性质、垂线段最短等知识点，正确找出两个全等三角形是解题关键．17．C【分析】证出OC＝BC，由等腰三角形的性质得CN⊥BD，①正确；证出MN是△AOB的中位线，得11MN∥AB，MN＝AB，由直角三角形的性质得NP＝CD，则MN＝NP，②正确；周长22四边形MNCP是平行四边形，无法证明四边形MNCP是菱形；③错误；由平行线的性质和等腰三角形的性质证出∠MND＝∠PND，则ND平分∠PNM，④正确；即可得出结论．【详解】解：∵四边形ABCD是平行四边形，1∴AB＝CD，AB∥CD，BC＝AD，OA＝OC＝AC，21∵AD＝AC，2∴OC＝BC，∵N是OB的中点，∴CN⊥BD，①正确；∵M、N分别是OA、OB的中点，∴MN是△AOB的中位线，1∴MN∥AB，MN＝AB，2∵CN⊥BD，∴∠CND＝90°，∵P是CD的中点，1∴NP＝CD＝PD＝PC，2∴MN＝NP，②正确；∵MN∥AB，AB∥CD，∴MN∥CD，又∵NP＝PC，MN＝NP， ∴MN＝PC，∴四边形MNCP是平行四边形，无法证明四边形MNCP是菱形；③错误；∵MN∥CD，∴∠PDN＝∠MND，∵NP＝PD，∴∠PDN＝∠PND，∴∠MND＝∠PND，∴ND平分∠PNM，④正确；正确的个数有3个，故选：C．【点睛】本题考查了平行四边形性质和判定，三角形中位线定理，直角三角形斜边上的中线性质，等腰三角形的性质等；熟练掌握三角形中位线定理、等腰三角形的性质、直角三角形斜边上的中线性质是解题的关键．18．B【分析】当点P和点A重合时，当点C和点Q重合时，PQ的值最大，当PQ⊥BC时，PQ的值最小，利用这两组数据，在Rt△ABQ中，可求得答案．【详解】当点P和点A重合时，当点C和点Q重合时，PQ的值最大，PQ85当PQ⊥BC时，PQ的值最小，∴PQ=8，∠Q=90°，在Rt△ACQ中，22CQ85816.在Rt△ABQ中，设AB=BC=x，则BQ=16-x，222222∴AQ+BQ=AB即8+（16-x）=x解之：x=10.故答案为：B．【点睛】本题考查菱形的性质和勾股定理的运用，解题关键是根据菱形的性质，判断出PQ最大和最小的情况． 19．A【分析】如图1，根据线段垂直平分线的性质得到PA=PD，QA=QD，则根据"SSS"可判断APQ≌DPQ，则可对甲进行判断；如图2，根据平行四边形的判定方法先证明四边形APDQ为平行四边形，则根据平行四边形的性质得到PA=DQ，PD=AQ，则根据"SSS"可判断△APQ≌△DQP,则可对乙进行判断.【详解】解：如图1，∵PQ垂直平分AD，∴PA=PD,，QA=QD，∵PQ=PQ，∴△APQ≌△DPQ(SSS)，所以甲正确；如图2，∵PD∥AQ，DQ∥AP，∴四边形APDQ为平行四达形，∴PA=DQ,，PD=AQ，∵PQ=QP，∴△APQ≌△DQP(SSS)，所以乙正确；故选：A.【点睛】本题考查了作图-复杂作图，复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作，也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定.20．B【分析】延长BG交CH于点E，根据正方形的性质证明△ABG≌△CDH≌△BCE，可得GE=BE-BG=2，HE=CH-CE=2，∠HEG=90°，从而由勾股定理可得GH的长．【详解】解：如图，延长BG交CH于点E， ∵四边形ABCD是正方形，∴∠ABC=90°，AB=CD=10，∵AG=8，BG=6，222∴AG+BG=AB，∴∠AGB=90°，∴∠1+∠2=90°，又∵∠2+∠3=90°，∴∠1=∠3，同理：∠4=∠6，在△ABG和△CDH中，AB＝CD＝10AG＝CH＝8BG＝DH＝6∴△ABG≌△CDH（SSS），∴∠1=∠5，∠2=∠6，∴∠2=∠4，在△ABG和△BCE中，∵∠1＝∠3，AB＝BC，∠2＝∠4，∴△ABG≌△BCE（ASA），∴BE=AG=8，CE=BG=6，∠BEC=∠AGB=90°，∴GE=BE－BG=8－6=2，同理可得HE=2，在Rt△GHE中，2222GHGEHE2222,故选：B．【点睛】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用，通过证三角形全等得出△GHE为直角三角形且能够求出两条直角边的长是解题的关键．21．C【分析】根据已知条件得到AB＝3，CD＝22，过A作AE∥CD交BC于E，则∠AEB＝∠DCB，根据平行四边形的性质得到CE＝AD，AE＝CD＝22，由已知条件得到∠BAE＝90°，根 22据勾股定理得到BE＝ABAE，于是得到结论．【详解】∵S1＝3，S3＝8∴AB＝3，CD＝22过A作AE∥CD交BC于E则∠AEB＝∠DCB∵AD∥BC∴四边形AECD是平行四边形∴CE＝AD，AE＝CD＝22∵∠ABC+∠DCB＝90°∴∠AEB+∠ABC＝90°∴∠BAE＝90°∴BE＝3811∵BC＝2AD∴BC＝2BE＝2112∴S2＝21144故选：C．【点睛】本题考查平行四边形的判定和性质，勾股定理，能正确作辅助线构造直角三角形是解决此题的关键．22．C【分析】正确的命题是真命题，根据矩形的判定定理，菱形的判定定理及平行四边形的判定定理依次判断.【详解】①对角线相等且互相平分的四边形是矩形，故该项错误；②四条边相等的四边形是菱形，故该项错误；③一组对边平行且相等的四边形是平行四边形，故该项正确； 故选：C.【点睛】此题考查真命题的定义，正确掌握矩形、菱形、平行四边形的判定定理是解题的关键.23．D【分析】①由矩形的性质得到OBC90，根据折叠的性质得到OBOD，PDOOBP90，BOPDOP，推出四边形OBPD是矩形，根据正方形的判定定理即可得到四边形OBPD为正方形；故①正确；②过D作DHOA于H，得到OA10，OB6，根据直角三角形的性质得到111DHOD3，根据三角形的面积公式得到OAD的面积为OADH31015，222故②正确；③连接OC，于是得到ODCDOC，即当ODCDOC时，CD取最小值，根据勾股定理得到CD的最小值为2346；故③正确；④根据已知条件推出P，D，A三点共线，根据平行线的性质得到OPBPOA，等量代换得到OPAPOA，求得APOA10，根据勾股定理得到BPBCCP1082，故④正确．【详解】解：①四边形OACB是矩形，OBC90，将OBP沿OP折叠得到OPD，OBOD，PDOOBP90，BOPDOP，BOP45，DOPBOP45，BOD90，BODOBPODP90，四边形OBPD是矩形，OBOD，四边形OBPD为正方形；故①正确；②过D作DHOA于H，点A(10,0)，点B(0,6)，OA10，OB6，ODOB6，BOPDOP30，DOA30，1DHOD3，211OAD的面积为OADH31015，故②正确；22③连接OC， 则ODCDOC，即当ODCDOC时，CD取最小值，ACOB6，OA10，2222OCOAAC106234，CDOCOD2346，即CD的最小值为2346；故③正确；④ODAD，ADO90，ODPOBP90，ADP180，P，D，A三点共线，OA//CB，OPBPOA，OPBOPD，OPAPOA，APOA10，AC6，22CP1068，BPBCCP1082，故④正确；故选：D．【点睛】本题考查了正方形的判定和性质，矩形的判定和性质，折叠的性质，勾股定理，三角形的面积的计算，正确的识别图形是解题的关键．24．B【分析】先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用面积法可求得AP最短时的长，然后即可求出AM最短时的长．【详解】解：连接AP，在ABC中，AB＝5，AC＝12，BC＝13，222∴AB+AC＝BC，∴∠BAC＝90°，∵PE⊥AB，PF⊥AC，∴四边形AFPE是矩形， ∴EF＝AP．∵M是EF的中点，1∴AM＝AP，2根据直线外一点到直线上任一点的距离，垂线段最短，即AP⊥BC时，AP最短，同样AM也最短，11∴S△ABC＝BCAPABAC，2211∴13AP512，2260∴AP最短时，AP＝，13130∴当AM最短时，AM＝AP＝．213故选：B．【点睛】此题主要考查学生对勾股定理逆定理的应用、矩形的判定和性质、垂线段最短和直角三角形斜边上的中线的理解和掌握，此题涉及到动点问题，有一定难度．25．B【分析】①只要证明OH是△DBF的中位线即可得出结论；11②根据OH是△BFD的中位线，得出GH=CF，由GH＜BC，可得出结论；241③易证得△ODH是等腰三角形，继而证得OD=BF；2④根据四边形ABCD是正方形，BE是∠DBC的平分线可求出Rt△BCE≌Rt△DCF，再由∠EBC=22.5°即可求出结论．【详解】解：∵EC=CF，∠BCE=∠DCF，BC=DC，∴△BCE≌△DCF，∴∠CBE=∠CDF，∵∠CBE+∠BEC=90°，∠BEC=∠DEH，∴∠DEH+∠CDF=90°，∴∠BHD=∠BHF=90°，∵BH=BH，∠HBD=∠HBF， ∴△BHD≌△BHF，∴DH=HF，∵OD=OB∴OH是△DBF的中位线∴OH∥BF；故①正确；1∴OH=BF，∠DOH=∠CBD=45°，2∵OH是△BFD的中位线，11∴DG=CG=BC，GH=CF，22∵CE=CF，11∴GH=CF=CE221∵CE＜CG=BC，21∴GH＜BC，故②错误．4∵四边形ABCD是正方形，BE是∠DBC的平分线，∴BC=CD，∠BCD=∠DCF，∠EBC=22.5°，∵CE=CF，∴Rt△BCE≌Rt△DCF（SAS），∴∠EBC=∠CDF=22.5°，∴∠BFH=90°-∠CDF=90°-22.5°=67.5°，∵OH是△DBF的中位线，CD⊥AF，∴OH是CD的垂直平分线，∴DH=CH，∴∠CDF=∠DCH=22.5°，∴∠HCF=90°-∠DCH=90°-22.5°=67.5°，∴∠CHF=180°-∠HCF-∠BFH=180°-67.5°-67.5°=45°，故④正确；∴∠ODH=∠BDC+∠CDF=67.5°，∴∠OHD=180°-∠ODH-∠DOH=67.5°，∴∠ODH=∠OHD，1∴OD=OH=BF；故③正确．2故选：B．【点睛】 此题考查了全等三角形的判定和性质、等腰三角形的判定与性质以及正方形的性质．解答此题的关键是作出辅助线，构造等腰直角三角形，利用等腰直角三角形的性质结合角平分线的性质逐步解答．26．D【分析】连接DE，因为点D是中点，所以CE等于4，根据勾股定理可以求出DE的长，过点M作MG⊥CD于点G，则由题意可知MG＝BC＝CD，证明△MNG≌△DEC，可以得到DE=MN，即可解决本题．【详解】解：如图，连接DE．由题意，在Rt△DCE中，CE＝4cm，CD＝8cm，由勾股定理得：DE＝22＝22＝45cm．CECD48过点M作MG⊥CD于点G，则由题意可知MG＝BC＝CD．连接DE，交MG于点I．由折叠可知，DE⊥MN，∴∠NMG+MIE＝90°，∵∠DIG+∠EDC＝90°，∠MIE＝∠DIG（对顶角相等），∴∠NMG＝∠EDC．在△MNG与△DEC中，NMGEDCMGCDMGNDCE90∴△MNG≌△DEC（ASA）．∴MN＝DE＝45cm．故选D．【点睛】本题主要考查了正方形的性质、折叠以及全等三角形，能够合理的作出辅助线并找出全等的条件是解决本题的关键．27．B【分析】由在ABC中，ABC和ACB的平分线相交于点O，根据角平分线的定义与三角形内1角和定理，即可求得②BOC90A正确；由平行线的性质和角平分线的定义得2出BEO和CFO是等腰三角形得出EFBECF故①正确；由角平分线定理与三角 1形面积的求解方法，即可求得③设ODm，AEAFn，则SAEFmn，故③错2误；E、F不可能是三角形ABC的中点，则EF不能为中位线故④正确．【详解】解：在ABC中，ABC和ACB的平分线相交于点O，11OBCABC，OCBACB，AABCACB180，221OBCOCB90A，21BOC180(OBCOCB)90A；故（2）正确；2在ABC中，ABC和ACB的平分线相交于点O，OBCOBE，OCBOCF，EF//BC，OBCEOB，OCBFOC，EOBOBE，FOCOCF，BEOE，CFOF，EFOEOFBECF，故（1）正确；过点O作OMAB于M，作ONBC于N，连接OA，在ABC中，ABC和ACB的平分线相交于点O，ONODOMm，1111SAEFSAOESAOFAEOMAFODOD(AEAF)mn；故（3）正确，2222（4）错误；11SEOBBEOM，SOCFFCOD，22OMOD，BE不一定等于CF，SEOB不一定等于SFOC．故（5）错误，综上可知其中正确的结论是（1）（2）（3），故选：B．【点睛】此题考查了三角形中位线定理的运用，以及平行线的性质、等腰三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用．28．B 【分析】首先证明AB=AF=AD，然后再证明∠AFG=90°，接下来，依据HL可证明△ABG≌△AFG，222得到BG=FG，再利用勾股定理得出GE=CG+CE，进而求出BG即可．【详解】解：在正方形ABCD中，AD=AB=BC=CD，∠D=∠B=∠BCD=90°，∵将△ADE沿AE对折至△AFE，∴AD=AF，DE=EF，∠D=∠AFE=90°，∴AB=AF，∠B=∠AFG=90°，又∵AG=AG，在Rt△ABG和Rt△AFG中，AG＝AGAB＝AF∴△ABG≌△AFG（HL）；∴BG=FG（全等三角形对应边相等），设BG=FG=x，则GC=6-x，∵E为CD的中点，∴CE=EF=DE=3，∴EG=3+x，222∴在Rt△CEG中，3+（6-x）=（3+x）（勾股定理），解得x=2，∴BG=2，故选B．【点睛】此题主要考查了勾股定理的综合应用、三角形全的判定和性质以及翻折变换的性质，根据翻折变换的性质得出对应线段相等是解题关键．29．D【分析】根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以2，可求出从A到A3变化后的坐标，再求出A1、A2、A3、A4、A5，继而得出A8坐标即可.【详解】解：根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘2，∵从A到A3经过了3次变化，3∵45°×3＝135°，1×2＝22，∴点A3所在的正方形的边长为22，点A3位置在第四象限，∴点A3的坐标是（2，－2），可得出：A1点坐标为（1，1）， A2点坐标为（0，2），A3点坐标为（2，－2），A4点坐标为（0，－4），A5点坐标为（－4，－4），A6（－8，0），A7（－8，8），A8（0，16），故选D.【点睛】本题考查了规律题，点的坐标，观察出每一次的变化特征是解答本题的关键.30．C【分析】222由ABACBC，得出∠BAC=90°，则①正确；由等边三角形的性质得∠DAB=∠EAC=60°，则∠DAE=150°，由SAS证得△ABC≌△DBF，得AC=DF=AE=4，同理△ABC≌△EFC（SAS），得AB=EF=AD=3，得出四边形AEFD是平行四边形，则②正确；由平行四边形的性质得∠DFE=∠DAE=150°，则③正确；∠FDA=180°－∠DFE=30°，过点A作11AMDF于点M，SAEFDDFAMDFAD436，则④不正确；即22可得出结果．【详解】222解：∵34=5，222∴ABACBC，∴∠BAC=90°，∴AB⊥AC，故①正确；∵△ABD，△ACE都是等边三角形，∴∠DAB=∠EAC=60°，又∴∠BAC=90°，∴∠DAE=150°，∵△ABD和△FBC都是等边三角形，∴BD=BA，BF=BC，∠DBF+∠FBA=∠ABC+∠ABF=60°，∴∠DBF=∠ABC，在△ABC与△DBF中，BDBADBFABC，BFBC∴△ABC≌△DBF（SAS），∴AC=DF=AE=4，同理可证：△ABC≌△EFC（SAS），∴AB=EF=AD=3，∴四边形AEFD是平行四边形，故②正确；∴∠DFE=∠DAE=150°，故③正确；∴∠FDA=180°-∠DFE=180°－150°=30°， 过点A作AMDF于点M，11∴SDFAMDFAD436，AEFD22故④不正确；∴正确的个数是3个，故选：C．【点睛】本题考查了平行四边形的判定与性质、勾股定理的逆定理、全等三角形的判定与性质、等边三角形的性质、平角、周角、平行是四边形面积的计算等知识；熟练掌握平行四边形的判定与性质是解题的关键．