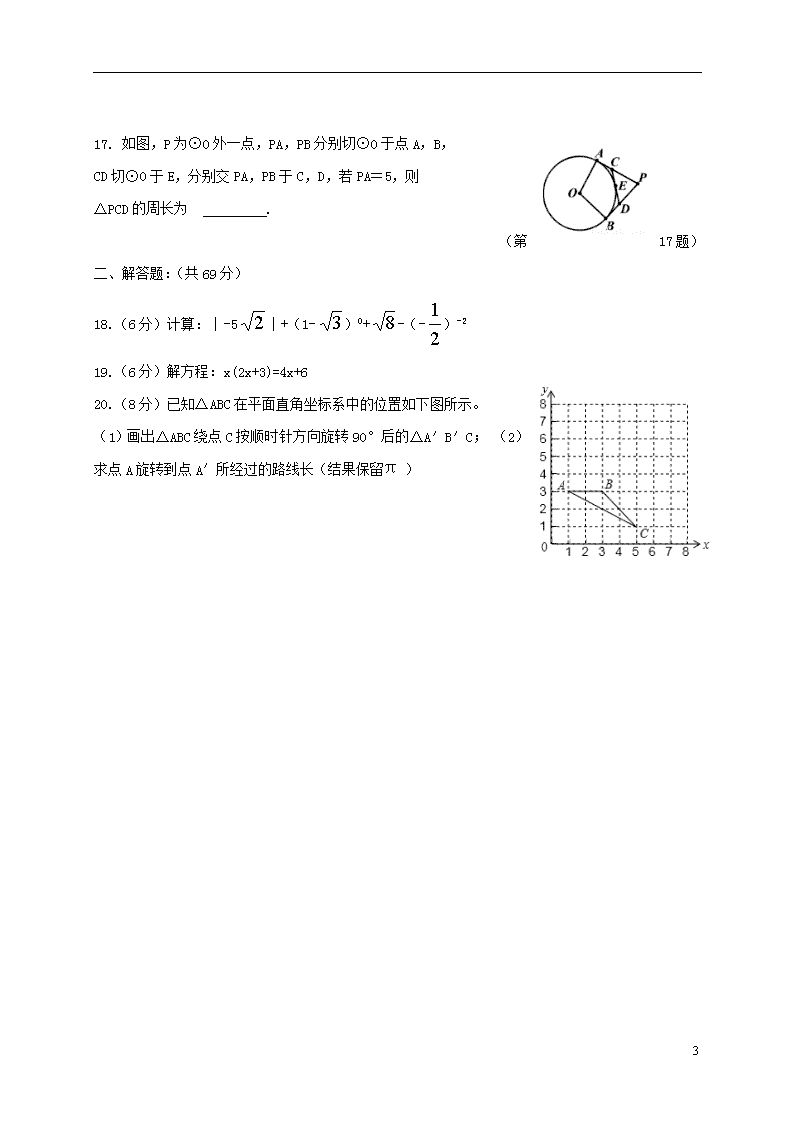内蒙古呼伦贝尔市海拉尔区2017届九年级数学上学期期末考试试题 11页

内蒙古呼伦贝尔市海拉尔区2017届九年级数学上学期期末考试试题一、选择题（每题3分，共36分）1.观察下列图形,既是轴对称图形又是中心对称图形的有(  )A.1个    B.2个    C.3个    D.4个2.下列事件中属于随机事件的是（）A．通常加热到100°时，水沸腾B．某射击运动员射击一次，命中靶心C．若a是实数，则|a|D．在一个仅装着白球和黑球的袋中摸球，摸出红球3.将抛物线y=5x2先向左平移2个单位，再向上平移3个单位后得到新的抛物线，则新抛物线的表达式是（ ）A．y=5（x﹣2）2+3   B．y=5（x+2）2+3  C．y=5（x﹣2）2﹣3   D．y=5（x+2）2﹣34.直线上有一点，则点关于原点的对称点的坐标是（）A.（-3,-6）B.（-6,3）C.（6,3）D.（-6,-3）5.如果反比例函数y=的图象经过点（﹣3，﹣4），那么函数的图象应在（ ）A．第一、三象限   B．第一、二象限   C．第二、四象限   D．第三、四象限6.若圆锥的侧面积为12π，它的底面半径为3cm,则此圆锥的母线长()A..2   B.3  C.4 D.67.在函数（为常数）的图象上有三点，，，则函数值的大小关系是()A．B.C.D.8.⊙O的半径为6，⊙O的一条弦AB长为4，以4为半径的同心圆与AB的关系是（）A.相离B.相切C.相交D.不能确定9.如图，四边形ABCD内接于半圆O，已知∠ADC=140°，则∠AOC的大小是（  ）A．40°    B．60°    C．70°    D．80°11 10.如图，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接正方形的面积为（  ）A．2    B．4      C．8      D．16-1Ox=1yx(第9题)（第10题）（第12题）11.生物兴趣小组的学生，将自己收集的标本向本组其他成员各赠送一件，全组共互赠了182件．如果全组共有x名同学，则根据题意列出的方程是()A．x（x+1）=182B．x（x+1）=182×C．x（x－1）=182D．x（x－1）=182×212.已知二次函数（）的图象如图所示，给出下列结论：①；②；③；④；其中正确的结论有(　　)A．1个B．2个C．3个D．4个二、填空题（每题3分，共15分）13.若是一元二次方程的一个解，则方程的另一个解是.   14.在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同。小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是.15.把二次函数y=x2-2x+4化为y=a(x-h)2+k的形式为.xyO（第16题）BAy＝y＝16.如图，点A在双曲线y＝上，点B在双曲线y＝上，且AB∥x轴，则△OAB的面积等于______．11 17.如图，P为⊙O外一点，PA，PB分别切⊙O于点A，B，CD切⊙O于E，分别交PA，PB于C，D，若PA＝5，则△PCD的周长为 .  （第17题）二、解答题：（共69分）18.（6分）计算：︱-5︱+（1-）0+-（-）-219.（6分）解方程：x(2x+3)=4x+620.（8分）已知△ABC在平面直角坐标系中的位置如下图所示。（1）画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C；（2）求点A旋转到点A′所经过的路线长（结果保留π）[]11 21.（9分）如图所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等．（1）现随机转动转盘一次，停止后，指针指向1的概率为 ；（2）小明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由．22.（9分）如图，已知正比例函数y=2x和反比例函数的图象交于点A（m，-2）．（1）求反比例函数的解析式；（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；（3）若双曲线上点C（2，n）沿OA方向平移个单位长度得到点B，判断四边形OABC的形状并证明你的结论． 11 23.（9分）如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．（1）求AC、AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由．24．(10分)某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为14米(如图所示)，设这个苗圃园垂直于墙的一边长为x米．(1)若苗圃园的面积为72平方米，求x；(2)若平行于墙的一边长不小于8米，这个苗圃园的面积S有最大值吗？如果有，求出最大值；如果没有，请说明理由；(3)当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围．[]14m苗圃园25.（12分）如图，在平面直角坐标系中，已知抛物线与x轴11 交于A，B两点，与y轴交于点C，直线L经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（－2，0），（6，－8）．（1）求抛物线的函数表达式，并分别求出点B和点E的坐标；（2）试探究抛物线上是否存在点F，使≌，若存在，请求出点F的坐标；若不存在，请说明理由； 11 2016—2017学年度上学期九年级期末检测试题答案题号123456789101112答案CBBAACDADACB二、填空题：13.X=214.16个15.y=(x-1)2+316.17.10三、解答题：18.解：原式＝5+1+2-4………………………4分＝7-3………………………6分19.x（2x+3）=4x+6（此题解法不唯一）解：x（2x+3）-2(2x+3)=0………………………2分(2x+3)(x-2)=0………………………4分x1=-,x2=2………………………6分20.解：（1）画出△A′B′C(图略)………………………4分（2）∵由图可知，AC==2∴点A旋转到点A′所经过的路线长为[]l＝π×2=π………………………8分21.解：(1)………………………2分（2）画出树状图或者列表（略）………………………5分由树状图（或列表）可知，所有等可能的情况有9种，………………6分其中两数之积为偶数的情况有5种，之积为奇数的情况有4种，11 ∴P（小明获胜）＝，P（小华获胜）＝，………………8分∵＞，∴该游戏不公平………………9分22.（1）设反比例函数的解析式为y=∵A（m，-2）在y=2x上，∴-2=2m，∴m=-1，∴A（-1，-2），………………1分又∵点A（-1.-2）在双曲线y=上，[]∴k=2，………………2分∴反比例函数的解析式为y=；………………3分（2）观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为-1＜x＜0或x＞1；………………5分（3）四边形OABC是菱形．………………6分证明：∵A（-1，-2），∴OA=，由题意知：CB∥OA且CB=，∴CB=OA，∴四边形OABC是平行四边形，………………8分∵C（2，n）在y=上，∴n=1，∴C（2，1），11 OC=，∴OC=OA，∵四边形OABC是平行四边形，∴四边形OABC是菱形．………………9分23.解：（1）如图，连接BD，………………1分∵AB是直径，∴∠ACB=∠ADB=90°，………………2分在Rt△ABC中，AC=（cm），………………3分②∵CD平分∠ACB，∴∠ACD=∠BCD，∴AD=BD，………………4分∴Rt△ABD是直角等腰三角形，∴AD=AB=×10=5cm；………………5分（2）直线PC与⊙O相切，………………6分理由：连接OC，∵OC=OA，∴∠CAO=∠OCA，∵PC=PE，11 ∴∠PCE=∠PEC，∵∠PEC=∠CAE+∠ACE，∵CD平分∠ACB，∴∠ACE=∠ECB，∴∠PCB=∠CAO=∠ACO，………………8分∵∠ACB=90°，∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°，即OC⊥PC，………………9分∴直线PC与⊙O相切．24.解：(1)苗圃园与墙平行的一边长为(30－2x)米．依题意可列方程x(30－2x)＝72，………………2分即x2－15x＋36＝0．解得x1＝3，x2＝12．………………3分(2)依题意，得8≤30－2x≤14．解得8≤x≤11．………………5分S＝x(30－2x)＝－2(x－)2＋………………6分∵抛物线开口向下，对称轴是直线x=又∵8≤x≤11∴在对称轴的右侧S随x的增大而减小………………7分当x＝8时，S有最大值，S最大＝112；………………8分(3)x的取值范围是5≤x≤10．………………10分25.解：（1）抛物线经过点A（－2，0），D（6，－8），解得…………………………2分∴抛物线的函数表达式为……………………………3分11 ，∴抛物线的对称轴为直线．又抛物线与x轴交于A，B两点，点A的坐标为（－2，0）．∴点B的坐标为（8，0）…………………4分设直线L的函数表达式为．点D（6，－8）在直线L上，∴6k=－8，解得．∴直线L的函数表达式为……………6分点E为直线L和抛物线对称轴的交点．∴点E的横坐标为3，纵坐标为，点E的坐标为（3，-4）………………7分（2）抛物线上存在点F，使≌．∵OE=CE=5∵点F在OC的垂直平分线上，此时点F的纵坐标为-4……………9分∴x2-3x-8=-4∴x=3±……………11分∴点F的坐标为（）或（）．……………12分11