第十五章 达朗贝尔原理(动静法).ppt 41页

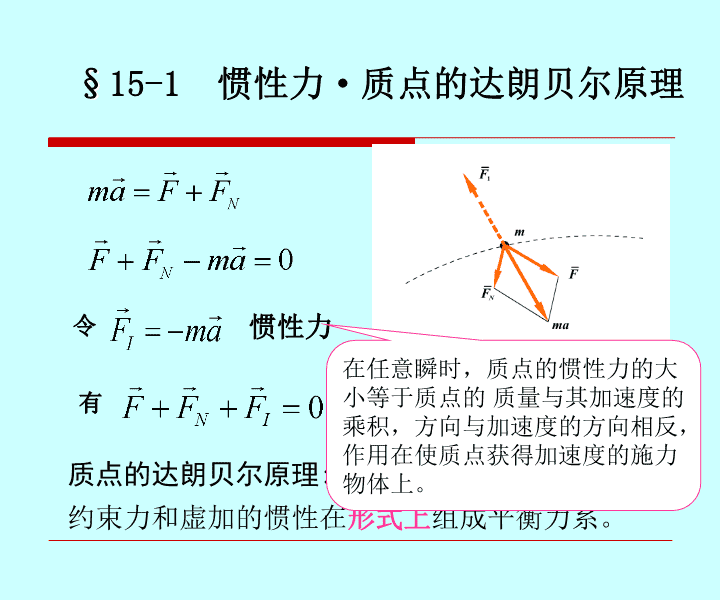
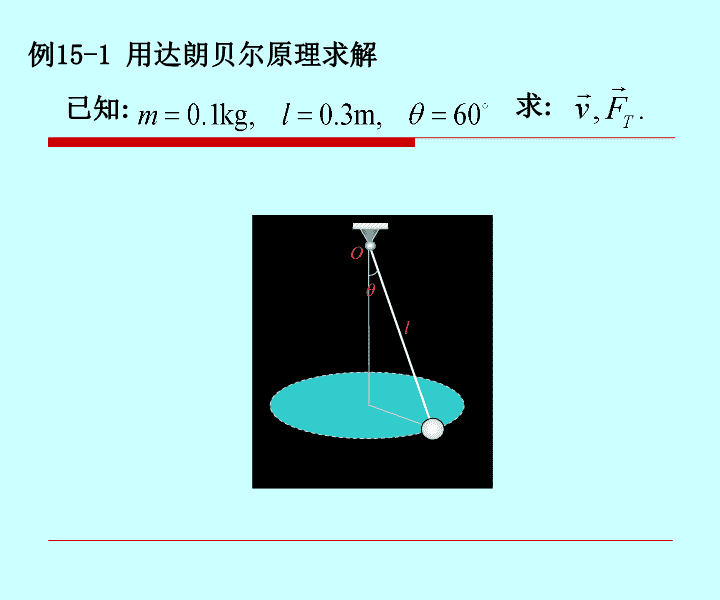
第十五章达朗贝尔原理(动静法)§15-1惯性力§15-2质点的达朗贝尔原理§15-3质点系的达朗贝尔原理§15-4刚体惯性力系的简化§15-5转子的静平衡与动平衡的概念动静法：用静力学中研究平衡问题的方法将动力学问题在形式上化为静力学问题来进行求解。 令惯性力有质点的达朗贝尔原理:作用在质点的主动力、约束力和虚加的惯性在形式上组成平衡力系。§15-1惯性力·质点的达朗贝尔原理在任意瞬时，质点的惯性力的大小等于质点的质量与其加速度的乘积，方向与加速度的方向相反，作用在使质点获得加速度的施力物体上。 例15-1用达朗贝尔原理求解已知:求:Olθ 解:解得先分析小球的受力和加速度，如图 §15-2质点系的达朗贝尔原理记为作用于第i个质点上外力的合力.为作用于第i个质点上内力的合力.则有 因有另一表述：作用在质点系上的外力与虚加在每个质点上的惯性力在形式上组成平衡力系。质点系的达朗贝尔原理：质点系中每个质点上作用的主动力，约束力和它的惯性力在形式上组成平衡力系. 例15-2如图所示,定滑轮的半径为r,质量为m均匀分布在轮缘上,绕水平轴Ｏ转动.垮过滑轮的无重绳的两端挂有质量为m1和m2的重物(m１>m2),绳与轮间不打滑,轴承摩擦忽略不计,求重物的加速度.OABr 解:由解得以系统为研究对象，加速度和受力分析如图。OABraam1gmgm2gFNy 球磨机是一种破碎机械，在鼓室中装进物料和钢球，如图所示。当鼓室绕水平轴转动时，钢球被鼓室携带到一定高度，此后脱离壳壁而沿抛物线轨迹落下，最后与物料碰撞以达到破碎的目的。如已知鼓室的转速为nrpm，直径为D。设钢球与壳壁间无滑动，试求最外层钢球的脱离角α。ωα例15-3 应用质点动静法设钢球的质量为m。钢球脱离壳壁的瞬时，壳壁对钢球的约束力FN=0。鼓室以匀角速度ω转动，钢球尚未脱离壳壁时，其加速度为：因此惯性力的大小为F*解：mgFNFαω 即脱离角α与鼓室转速n有关。求得这就是钢球在任一位置θ时所受的法向动约束力，显然当钢球脱离壳壁时，FN=0，由此可求出其脱离角α为mgFNFαω §15-3刚体惯性力系的简化１刚体平移惯性力系向质心简化.只简化为一个力2刚体定轴转动大小为:由 由有记为对于z轴的惯性积.同理 如果刚体有质量对称面且该面与转动轴垂直,简化中心取此平面与转轴的交点,则有３　刚体作平面运动（平行于质量对称面）因 例15-4质量为m，长l的匀质细直杆AB，其A端铰接在铅直轴Az上，并以匀角速度ω绕该轴转动。求当AB与转轴间的夹角θ=常量(图a)时ω与θ的关系，以及铰链A的约束力。ξmgF*FAzFAx(a)(b) 取杆AB作为研究对象。受力如图(b)。显然当θ不变时，杆上各点只有向心加速度an，方向都为水平并指向转轴；这样，杆的惯性力是同向平行分布力，如图(b)所示。解：ξmgF*FAzFAx(a)(b)因而惯性力的元素是沿杆AB取任一微小段dξ考虑，它的质量是mgdξ/gl，加速度是ω2ξsinθ。 全杆惯性力合力的大小可用积分求出设合力F*的作用线与杆AB的交点是D，并以b代表D到A的距离，则ξmgF*FAzFAx 由对点A的合力矩定理，有把式(1)代入式(2)，即可求得ξmgF*FAzFAx 写出杆的动态平衡方程，有把表达式(1)代入平衡方程(3)，有即（3）（4）（5）ξmgF*FAzFAx 从而求得显然,第二个解只在3g/2lω2≤1时成立。第一个解能否成立，还需进一步分析。利用(4)，(5)，可以求得铰链上的反作用力，有第5章达朗伯原理ξmgF*FAzFAx 例15-5如图所示,电动机定子及其外壳总质量为m1,质心位于O处.转子的质量为m2,质心位于Ｃ处,偏心矩ＯＣ＝e,图示平面为转子的质量对称面.电动机用地角螺钉固定于水平基础上,转O与水平基础间的距离为h.运动开始时,转子质心Ｃ位于最低位置,转子以匀角速度　转动.求:基础与地角螺钉给电动机总的约束力.xyωm1gm2gCOhφ 解:因以电动机为研究对象，如图 例15-6如图所示,电动绞车安装在梁上,梁的两端搁在支座上,绞车与梁共重为P.绞盘半径为R,与电机转子固结在一起,转动惯量为J,质心位于O处.绞车以加速度a提升质量为m的重物,其它尺寸如图.已知:求:支座A，B受到的附加约束力。ABxyal1l2l3mgWα 解:解得:以绞车和梁一起为研究对象ABxyal1l2l3mgF*WFAFBαM* 上式中前两项为静约束力，附加动约束力为附加压力（或附加动约束力）决定于惯性力系，只求附加压力时，列方程不必考虑重力。 均质圆盘质量为mA，半径为r。细长杆长l=2r，质量为m。杆端A点与轮心为光滑铰接，如图所示。如在A处加一水平拉力F，使轮沿水平面滚动。问F力多大能使杆的B端刚刚离开地面？又为保证纯滚动，轮与地面间的静滑动摩擦系数应为多大？mAgmgFABC例题5-7 细杆刚离地面时仍为平动，而地面约束力为零，设其加速度为a。以杆为研究对象，杆承受的力并加上惯性力如图所示，其中F*C=ma。整个系统承受的力并加上惯性力如图，其中F*A=mAa,由方程得解出ABCF*CmgFAxFAya解：按动静法列出方程mAgmgFABCF*AF*CM* 为求摩擦力，应以圆轮为研究对象。由方程，得地面摩擦力解得mAgmgFABCFNF*AF*CM*Fs≤mAgFAFNF*AM*Fs 再以整个系统为研究对象，由方程，得由此，地面摩擦系数AFNF*AF*CmAgmgFBCM*Fs≥mAgFAFNF*AM*Fs §15-4转子的静平衡与动平衡的概念 解得 即:必有通过质心的惯性主轴称为中心惯性主轴因此，避免出现轴承动约束力的条件是：刚体的转轴应是刚体的中心惯性主轴.引起的轴承约束力称动约束力由称满足的轴z为惯性主轴动约束力为零的条件为: 转子的静平衡：设刚体的转轴通过质心，且刚体除重力外，没有受到其它主动力作用，则刚体可以在任意位置静止不动，这种现象称为静平衡。转子的动平衡：当刚体的转轴通过质心且为惯性主轴时，刚体转动时不出现轴承附加动反力，这种现象称为动平衡。转子的静平衡与动平衡的概念 飞轮质量为m，半径为R，以匀角速度ω转动。设轮缘较薄，质量均匀分布，轮辐质量不计。若不靠考虑重力的影响，求轮缘横截面的张力。例题5-8 取四分之一轮缘为研究对象，如图所示。将轮缘分成无数微小的弧段，每段加惯性力建立平衡方程令，有xyθ∆θRABOFAFB解： 由于轮缘质量均分布，任一截面张力都相同。再建立平衡方程同样解得xyθ∆θRABOFAFB 半径为R，重量为W1的大圆轮，由绳索牵引，在重量为W2的重物A的作用下，在水平地面上作纯滚动，系统中的小圆轮重量忽略不计。求大圆轮与地面之间的滑动摩擦力。AOCW1W2R例题5-9 解：考察整个系统，有4个未知约束力。如果直接采用动静法，需将系统拆开。因为系统为一个自由度，所以考虑先应用动能定理，求出加速度，再对大圆轮应用动静法。1.应用动能定理。AOCW1W2RFFNFOxFOy 1.应用动能定理。两边对时间t求导，且得AOCW1W2RFFNFOxFOy 2.应用动静法。取轮子为研究对象。CFFNJCαW1a将带入上式得FOxAOCW1W2RFFNFOy 作业：P205～P2125－11、5－16、5－17