郝桐生--第15章 达朗贝尔原理(例题).pdf 24页

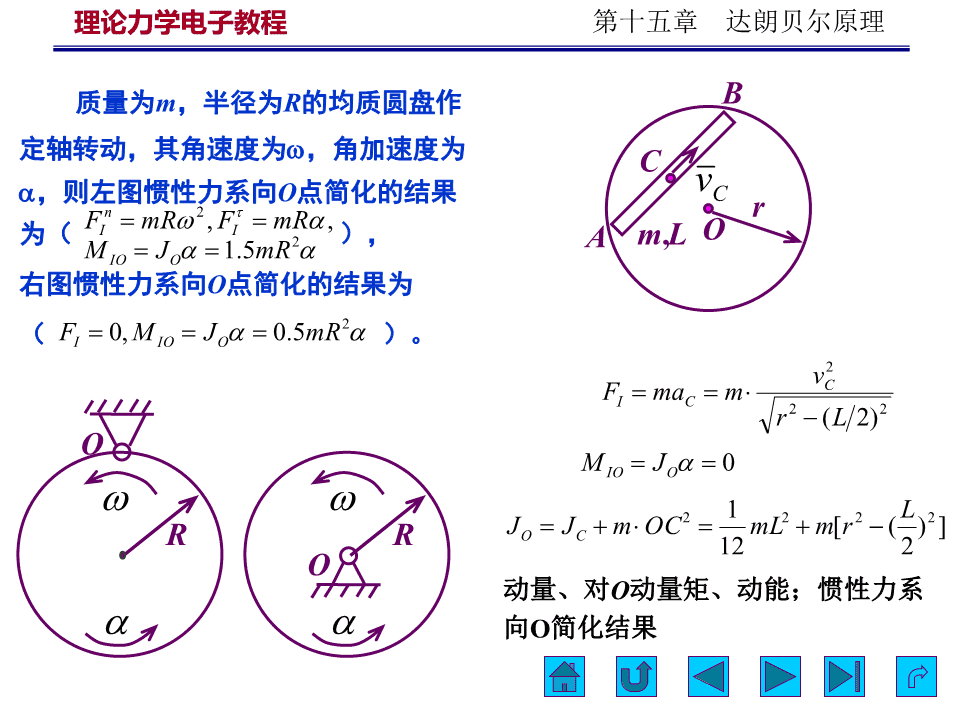
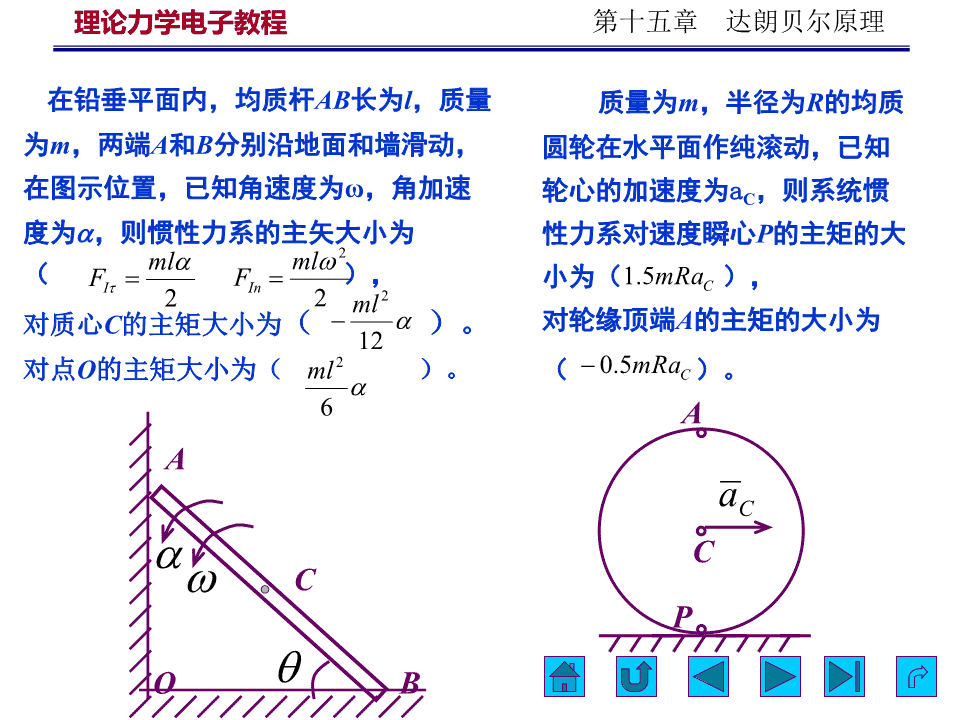
理论力学电子教程第十五章达朗贝尔原理质量为m，半径为R的均质圆盘作B定轴转动，其角速度为，角加速度为Cv，则左图惯性力系向O点简化的结果Cn2rFmR,FmR,为（II），m,LO2AMJ1.5mRIOO右图惯性力系向O点简化的结果为2（FI0,MIOJO0.5mR）。2vFmamCIC22r(L2)OMJ0IOO1L2222JJmOCmLm[r()]RROC122O动量、对O动量矩、动能；惯性力系向O简化结果 理论力学电子教程第十五章达朗贝尔原理在铅垂平面内，均质杆AB长为l，质量质量为m，半径为R的均质为m，两端A和B分别沿地面和墙滑动，圆轮在水平面作纯滚动，已知在图示位置，已知角速度为ω，角加速轮心的加速度为aC，则系统惯度为，则惯性力系的主矢大小为性力系对速度瞬心P的主矩的大2mlml（FIFIn），小为（1.5mRaC），22ml2对质心C的主矩大小为（）。对轮缘顶端A的主矩的大小为12对点O的主矩大小为（ml2）。（0.5mRa）。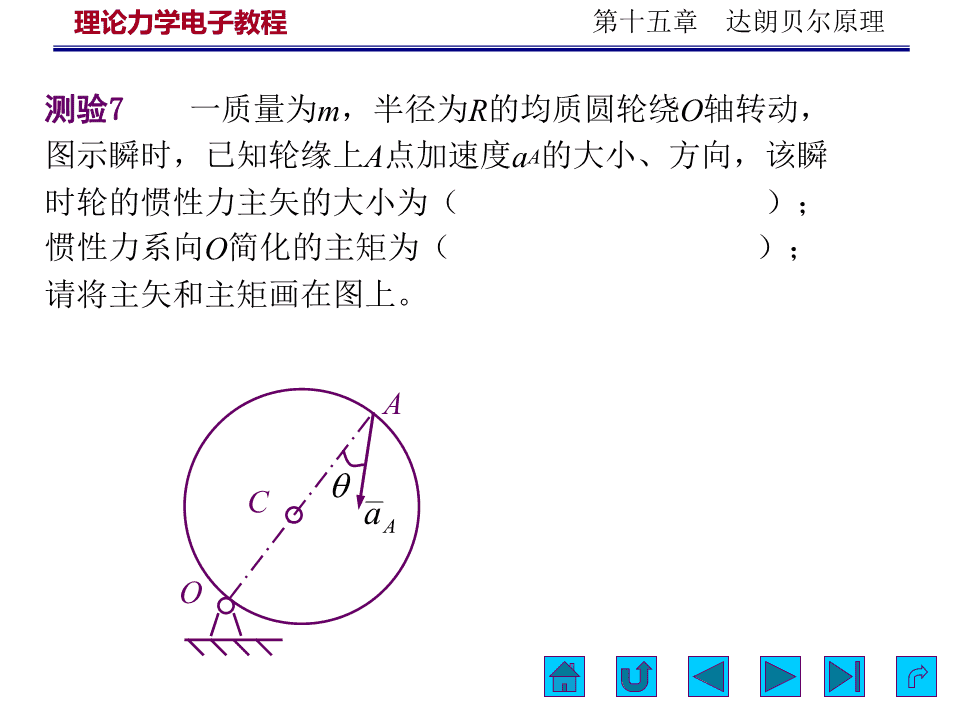C6AAaCCCPOB 理论力学电子教程第十五章达朗贝尔原理测验7一质量为m，半径为R的均质圆轮绕O轴转动，图示瞬时，已知轮缘上A点加速度aA的大小、方向，该瞬时轮的惯性力主矢的大小为（）；惯性力系向O简化的主矩为（）；请将主矢和主矩画在图上。ACaAO 理论力学电子教程第十五章达朗贝尔原理机车的连杆AB的质量为m，两端用铰链连接于主动轮上，铰链到轮心的距离均为r，主动轮的半径均为R。求当机车以匀速v直线前进时，铰链对连杆的水平作用力的合力，及A、B处的竖向约束力（用动静法求解）。BArCrvRO1O2 理论力学电子教程第十五章达朗贝尔原理20170606[例15-1]均质杆长l,质量m,与水平面铰接,杆从与平面成0角位置静止落下。求开始落下时杆AB的角加速度及A点支座反力。解：（法1）选杆AB为研究对象，虚加惯性力系：注意定轴转动刚体的惯性力虚加于转轴上。2mlnmlFIRFIRman0,MIAJA23根据动静法，有F0,FAmgcos0FIA0(1)nnFn0,FAmgsin0FIA0(2)MA(F)0,mgl/2cos0MIA0(3)n由(2)得:Fmgsin;A03g由(3)得:cos;02lmg代入(1)得:Fcos。A04 理论力学电子教程第十五章达朗贝尔原理法2：用动量矩定理+质心运动定理再求解此题：解：选AB为研究对象，由动量矩定理，得：lmgcosl203gJAmgcos0cos02122lml33gt0时,0,cos0,此时02l由质心运动定理：这里maFmgcosl3gCA0acosC024nn0mamgsinFC0Anmg所以Fmgsin,FcosA0A04 理论力学电子教程第十五章达朗贝尔原理置于水平地面上的半圆柱质量为m，半径为r，质心C距圆心O的距离为e，对过质心C且垂直于纸面的轴的转动惯量为J。如半圆柱于图示位置（OC水平）从静止开始运动，不计摩擦，求：（1）试用动力学普遍定理方法求初瞬时半圆柱的角加速度；（2）试用达朗伯原理（动静法）求初瞬时半圆柱的角加速度；（3）用动力学普遍定理求质心C运动到最低位置时半圆柱的角速度。eOCrA 理论力学电子教程第十五章达朗贝尔原理质量不计的圆环如图，在径向焊接一个质量为m，长为r的均质细棒，圆环可在水平面上纯滚动，在图示位置细棒OA水平，从静止开始运动，试用达朗伯原理（动静法）求细棒OA在图示位置的角加速度和地面对圆环的摩擦力。OAP 理论力学电子教程第十五章达朗贝尔原理1P2例13－3已知：PP;P;r;Jr,求。ABO2g【解】(1)取整个系统为研究对象，(e)受力分析如图示。MOPArPBr(PAPB)rPP运动分析：v=ｒABLvrvrJOOgg21P2rP将Jr代入,得L(PP)OOAB2gg2dr2P由动量矩定理：[(PP)](PP)rABABdtg2dgPPABdtrPPP/2AB 理论力学电子教程第十五章达朗贝尔原理例13-12均质圆柱体A和B的重量均为P，半径均为r，一绳缠在绕固定轴O转动的圆柱A上，绳的另一端绕在圆柱B上，绳重不计且不可伸长，不计轴O处摩擦。求：圆柱B下落时质心的加速度。 理论力学电子教程第十五章达朗贝尔原理解：（1）选圆柱A为研究对象1P2rATr（1）2g（2）选圆柱B为研究对象1P2rBT"r（2）2gPaCPT"（3）g（3）运动学关系：aaarr（4）CerAB由（1）、（2）式得：AB代入（3）、（4）并结合（2）式得：2g4aCgAB55r 理论力学电子教程第十五章达朗贝尔原理1P2例13－3已知：PP;P;r;Jr,求。ABO2g【解】(1)取整个系统为研究对象，(e)受力分析如图示。MOPArPBr(PAPB)rPP运动分析：v=ｒABLvrvrJOOgg21P2rP将Jr代入,得L(PP)OOAB2gg2dr2P由动量矩定理：[(PP)](PP)rABABdtg2 理论力学电子教程第十五章达朗贝尔原理[例15-4]质量为m1和m2的两均质重物，分别挂在两条绳子上，绳又分别绕在半径为r1和r2并装在同一轴的两鼓轮上，已知两鼓轮对于转轴O的转动惯量为J，系统在重力作用下发生运动，求鼓轮的角加速度（轴O处摩擦不计，绳与轮无相对滑动）。 理论力学电子教程第十五章达朗贝尔原理解：方法1用达朗伯原理求解取系统为研究对象，虚加惯性力和惯性力偶：Fma,Fma,MJJI111I222IOO由动静法：MO(F)0,mgrmgrFrFrM01122I11I22IOmgrmgrmarmarJ01122111222列补充方程：a1r1,a2r2代入上式mrmr1122g22mrmrJ1122 理论力学电子教程第十五章达朗贝尔原理方法2用动量矩定理求解取系统为研究对象LmvrmvrJO11122222(mrmrJ)1122(e)M(F)mgrmgrO1122根据动量矩定理：d22[(m1r1m2r2J)]m1gr1m2gr2dtmrmr1122所以g22mrmrJ1122 理论力学电子教程第十五章达朗贝尔原理方法3用动能定理求解取系统为研究对象，任一瞬时系统的212121222TmvmvJ(mrmrJ)2112211222222任意假定一个初始值TC(某确定值)1Wmgsmgsmgrmgr1211221122(mr-mr)g1122由T2T1W12，得222(mrmrJ)C(mrmr)g112211222两边对时间t求导数，得dω22dω(mrmrJ)(mrmr)g11221122dtdtdmrmr1122g22dtmrmrJ1122 理论力学电子教程第十五章达朗贝尔原理[例15-5]在图示机构中，沿斜面向上作纯滚动的圆柱体和鼓轮O均为均质物体，各重为G和Q，半径均为R，绳子不可伸长，其质量不计，绳与轮之间无相对滑动，斜面倾角，如在鼓轮上作用一常力偶矩M，试求：(1)鼓轮的角加速度？(2)绳子的拉力？(3)轴承O处的约束力？(4)圆柱体与斜面间的摩擦力（不计滚动摩擦）？ 理论力学电子教程第十五章达朗贝尔原理解：方法一用动静法求解1Q2MJR（1）取轮O为研究对象，虚加惯性力偶IOOOO2g列出动静法方程：MO(F)0,FTRMIOM0(1)Fx0,FOxFTcos0(2)Fy0,FOyQFTsin0(3)（2）取轮A为研究对象，虚加惯性力FIR和惯性力偶MIC如图示。GFa,IAAg1G2MRIAA2g 理论力学电子教程第十五章达朗贝尔原理列出动静法方程：MC(F)0,GsinRFIARFTRMIA0(4)Fx0,FTFIAFSGsin0(5)Fy0,FNGcos0(6)运动学关系：aARAROAO将MIA，FIA，MIA及运动学关系代入到(1)和(4)式并联立求解得：2(MPsinR)G(3MQRsin)O2gFT(Q3G)R(Q3G)R代入(2)、(3)、(5)式，得：G(3MQRsin)Fcos,Ox(Q3G)RG(3MQRsin)FsinQ,Oy(Q3G)RG(MGRsin)F。S(Q3G)R 理论力学电子教程第十五章达朗贝尔原理方法二用动力学普遍定理求解(1)用动能定理求鼓轮角加速度。W12MPRsin(MPRsin)TC(常量)121Q221P21P22O2TRvR(Q3P)R2OA22g2g22g4g(vRωRω)两边对t求导数：OA由T2T1W12，得2O2(Q3P)RC(MPRsin)4g12(Q3P)R2(MPRsin)OOO4g2(MPRsin)gO2(Q3P)R 理论力学电子教程第十五章达朗贝尔原理(2)用动量矩定理求绳子拉力（定轴转动微分方程）取轮O为研究对象，由动量矩定理得Q2P(3MQRsin)RMTRFOT2g(Q3P)R(3)用质心运动定理求解轴承O处约束力取轮O为研究对象，根据质心运动定理：MaCxFx,0FOxFTcosMaCyFy,0FOyQFTsinP(3MQRsin)FcosOx(Q3P)RP(3MQRsin)FsinQOy(Q3P)R 理论力学电子教程第十五章达朗贝尔原理(4)用刚体平面运动微分方程求摩擦力取圆柱体A为研究对象，根据刚体平面运动微分方程JαFR(αα)AASAOJAA1P22(MPRsin)P(MPRsin)FRgS2RR2g(Q3P)R(Q3P)R方法三：用动能定理求鼓轮的角加速度用达朗贝尔原理求约束力（绳子拉力、轴承FTO处反力和FOx及摩F擦Oy力）。FS 理论力学电子教程第十五章达朗贝尔原理均质棒AB得质量为m=4kg，其两端悬挂在两条平行绳例15-7上，棒处在水平位置，如图（a）所示。其中一绳BD突然断了，求此瞬时AC绳得张力F。CDFFIRyMaaCICAAFIRx()mgaABCA(a)(b)【解】当BD绳断了以后，棒开始作平面运动，则惯性力系的简化中心在质心C上。因瞬时系统的速度特征量均为零，则点加速度为a。以A为基点，有AnnaaaaaaCACACAACA 理论力学电子教程第十五章达朗贝尔原理nnaaaaaaCACACAACAl其中aCA,l为棒长。2虚加惯性力系，如图（b）所示，有mlMJ，Fma，FICCIRxAIRy2lmll则mA(F)0，mgJC0222123g因JCml，得122lml又Fy0，Fmg021得Fmg9.8N4